HMAR: Efficient Hierarchical Masked Auto-Regressive Image Generation

Visual Auto-Regressive modeling (VAR) has shown promise in bridging the speed and quality gap between autoregressive image models and diffusion models. VAR reformulates autoregressive modeling by decomposing an image into successive resolution scales. During inference, an image is generated by predicting all the tokens in the next (higher-resolution) scale, conditioned on all tokens in all previous (lower-resolution) scales. However, this formulation suffers from reduced image quality due to the parallel generation of all tokens in a resolution scale; has sequence lengths scaling superlinearly in image resolution; and requires retraining to change the sampling schedule. We introduce Hierarchical Masked Auto-Regressive modeling (HMAR), a new image generation algorithm that alleviates these issues using next-scale prediction and masked prediction to generate high-quality images with fast sampling. HMAR reformulates next-scale prediction as a Markovian process, wherein the prediction of each resolution scale is conditioned only on tokens in its immediate predecessor instead of the tokens in all predecessor resolutions. When predicting a resolution scale, HMAR uses a controllable multi-step masked generation procedure to generate a subset of the tokens in each step. On ImageNet 256x256 and 512x512 benchmarks, HMAR models match or outperform parameter-matched VAR, diffusion, and autoregressive baselines. We develop efficient IO-aware block-sparse attention kernels that allow HMAR to achieve faster training and inference times over VAR by over 2.5x and 1.75x respectively, as well as over 3x lower inference memory footprint. Finally, HMAR yields additional flexibility over VAR; its sampling schedule can be changed without further training, and it can be applied to image editing tasks in a zero-shot manner.

RECON: Robust symmetry discovery via Explicit Canonical Orientation Normalization

Real-world data often exhibits unknown or approximate symmetries, yet existing equivariant networks must commit to a fixed transformation group prior to training, e.g., continuous $SO(2)$ rotations. This mismatch degrades performance when the actual data symmetries differ from those in the transformation group. We introduce RECON, a framework to discover each input's intrinsic symmetry distribution from unlabeled data. RECON leverages class-pose decompositions and applies a data-driven normalization to align arbitrary reference frames into a common natural pose, yielding directly comparable and interpretable symmetry descriptors. We demonstrate effective symmetry discovery on 2D image benchmarks and -- for the first time -- extend it to 3D transformation groups, paving the way towards more flexible equivariant modeling.

Cosmos-Reason1: From Physical Common Sense To Embodied Reasoning

Physical AI systems need to perceive, understand, and perform complex actions in the physical world. In this paper, we present the Cosmos-Reason1 models that can understand the physical world and generate appropriate embodied decisions (e.g., next step action) in natural language through long chain-of-thought reasoning processes. We begin by defining key capabilities for Physical AI reasoning, with a focus on physical common sense and embodied reasoning. To represent physical common sense, we use a hierarchical ontology that captures fundamental knowledge about space, time, and physics. For embodied reasoning, we rely on a two-dimensional ontology that generalizes across different physical embodiments. Building on these capabilities, we develop two multimodal large language models, Cosmos-Reason1-8B and Cosmos-Reason1-56B. We curate data and train our models in four stages: vision pre-training, general supervised fine-tuning (SFT), Physical AI SFT, and Physical AI reinforcement learning (RL) as the post-training. To evaluate our models, we build comprehensive benchmarks for physical common sense and embodied reasoning according to our ontologies. Evaluation results show that Physical AI SFT and reinforcement learning bring significant improvements. To facilitate the development of Physical AI, we will make our code and pre-trained models available under the NVIDIA Open Model License at https://github.com/nvidia-cosmos/cosmos-reason1.

Meshtron: High-Fidelity, Artist-Like 3D Mesh Generation at Scale

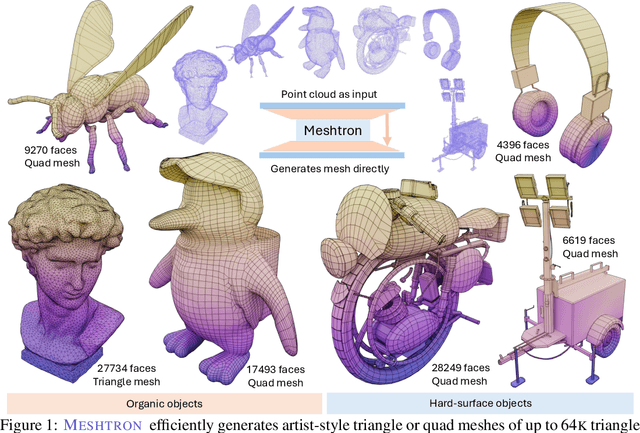
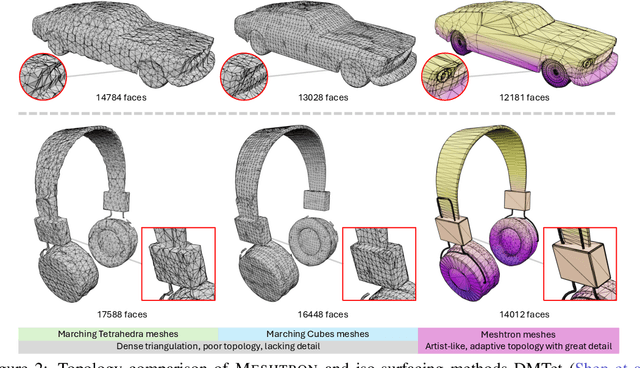
Meshes are fundamental representations of 3D surfaces. However, creating high-quality meshes is a labor-intensive task that requires significant time and expertise in 3D modeling. While a delicate object often requires over $10^4$ faces to be accurately modeled, recent attempts at generating artist-like meshes are limited to $1.6$K faces and heavy discretization of vertex coordinates. Hence, scaling both the maximum face count and vertex coordinate resolution is crucial to producing high-quality meshes of realistic, complex 3D objects. We present Meshtron, a novel autoregressive mesh generation model able to generate meshes with up to 64K faces at 1024-level coordinate resolution --over an order of magnitude higher face count and $8{\times}$ higher coordinate resolution than current state-of-the-art methods. Meshtron's scalability is driven by four key components: (1) an hourglass neural architecture, (2) truncated sequence training, (3) sliding window inference, (4) a robust sampling strategy that enforces the order of mesh sequences. This results in over $50{\%}$ less training memory, $2.5{\times}$ faster throughput, and better consistency than existing works. Meshtron generates meshes of detailed, complex 3D objects at unprecedented levels of resolution and fidelity, closely resembling those created by professional artists, and opening the door to more realistic generation of detailed 3D assets for animation, gaming, and virtual environments.

The Good, The Efficient and the Inductive Biases: Exploring Efficiency in Deep Learning Through the Use of Inductive Biases

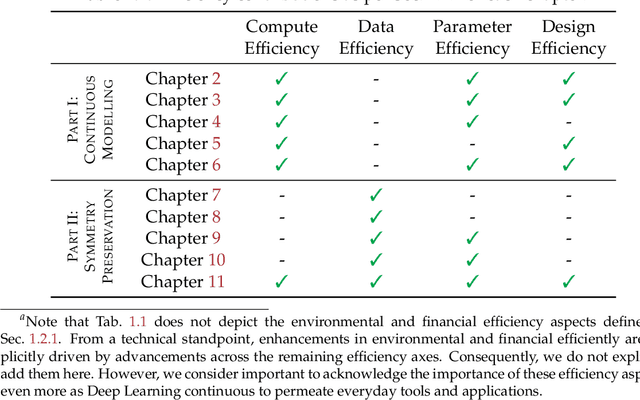
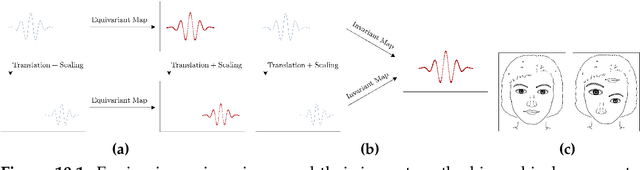
The emergence of Deep Learning has marked a profound shift in machine learning, driven by numerous breakthroughs achieved in recent years. However, as Deep Learning becomes increasingly present in everyday tools and applications, there is a growing need to address unresolved challenges related to its efficiency and sustainability. This dissertation delves into the role of inductive biases -- particularly, continuous modeling and symmetry preservation -- as strategies to enhance the efficiency of Deep Learning. It is structured in two main parts. The first part investigates continuous modeling as a tool to improve the efficiency of Deep Learning algorithms. Continuous modeling involves the idea of parameterizing neural operations in a continuous space. The research presented here demonstrates substantial benefits for the (i) computational efficiency -- in time and memory, (ii) the parameter efficiency, and (iii) design efficiency -- the complexity of designing neural architectures for new datasets and tasks. The second focuses on the role of symmetry preservation on Deep Learning efficiency. Symmetry preservation involves designing neural operations that align with the inherent symmetries of data. The research presented in this part highlights significant gains both in data and parameter efficiency through the use of symmetry preservation. However, it also acknowledges a resulting trade-off of increased computational costs. The dissertation concludes with a critical evaluation of these findings, openly discussing their limitations and proposing strategies to address them, informed by literature and the author insights. It ends by identifying promising future research avenues in the exploration of inductive biases for efficiency, and their wider implications for Deep Learning.

Self-Supervised Detection of Perfect and Partial Input-Dependent Symmetries

Group equivariance ensures consistent responses to group transformations of the input, leading to more robust models and enhanced generalization capabilities. However, this property can lead to overly constrained models if the symmetries considered in the group differ from those observed in data. While common methods address this by determining the appropriate level of symmetry at the dataset level, they are limited to supervised settings and ignore scenarios in which multiple levels of symmetry co-exist in the same dataset. For instance, pictures of cars and planes exhibit different levels of rotation, yet both are included in the CIFAR-10 dataset. In this paper, we propose a method able to detect the level of symmetry of each input without the need for labels. To this end, we derive a sufficient and necessary condition to learn the distribution of symmetries in the data. Using the learned distribution, we generate pseudo-labels that allow us to learn the levels of symmetry of each input in a self-supervised manner. We validate the effectiveness of our approach on synthetic datasets with different per-class levels of symmetries e.g. MNISTMultiple, in which digits are uniformly rotated within a class-dependent interval. We demonstrate that our method can be used for practical applications such as the generation of standardized datasets in which the symmetries are not present, as well as the detection of out-of-distribution symmetries during inference. By doing so, both the generalization and robustness of non-equivariant models can be improved. Our code is publicly available at https://github.com/aurban0/ssl-sym.

Laughing Hyena Distillery: Extracting Compact Recurrences From Convolutions

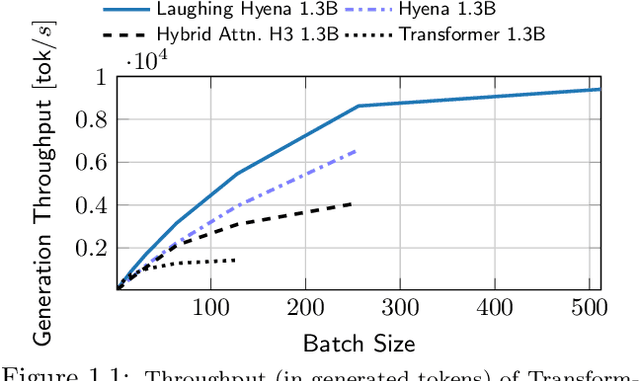
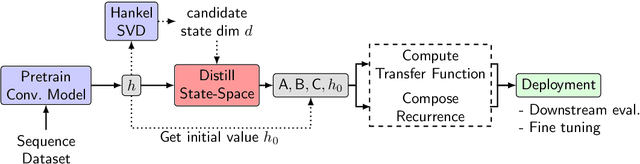
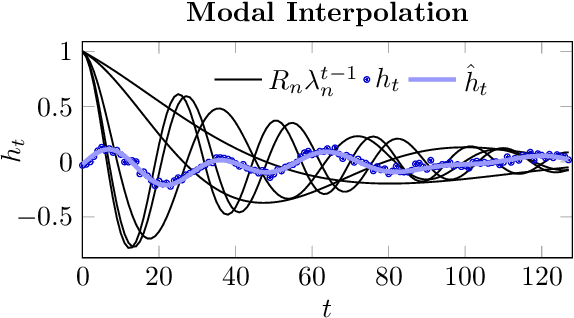
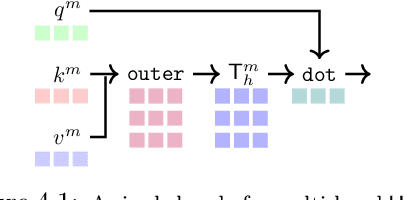
Recent advances in attention-free sequence models rely on convolutions as alternatives to the attention operator at the core of Transformers. In particular, long convolution sequence models have achieved state-of-the-art performance in many domains, but incur a significant cost during auto-regressive inference workloads -- naively requiring a full pass (or caching of activations) over the input sequence for each generated token -- similarly to attention-based models. In this paper, we seek to enable $\mathcal O(1)$ compute and memory cost per token in any pre-trained long convolution architecture to reduce memory footprint and increase throughput during generation. Concretely, our methods consist in extracting low-dimensional linear state-space models from each convolution layer, building upon rational interpolation and model-order reduction techniques. We further introduce architectural improvements to convolution-based layers such as Hyena: by weight-tying the filters across channels into heads, we achieve higher pre-training quality and reduce the number of filters to be distilled. The resulting model achieves 10x higher throughput than Transformers and 1.5x higher than Hyena at 1.3B parameters, without any loss in quality after distillation.

Learned Gridification for Efficient Point Cloud Processing

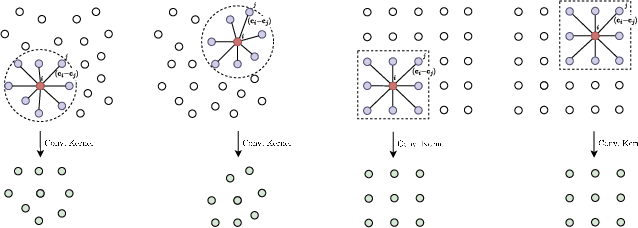
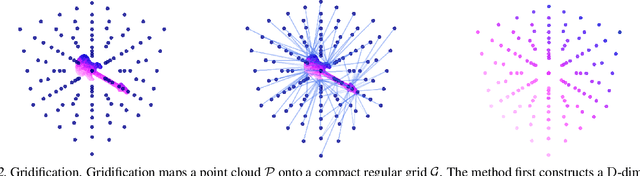
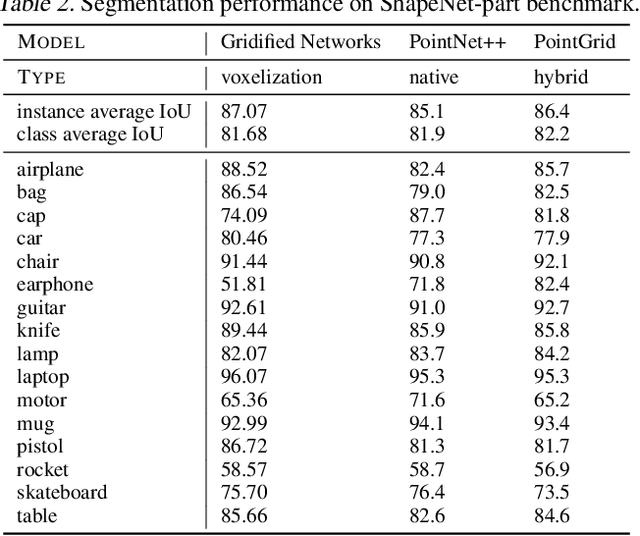
Neural operations that rely on neighborhood information are much more expensive when deployed on point clouds than on grid data due to the irregular distances between points in a point cloud. In a grid, on the other hand, we can compute the kernel only once and reuse it for all query positions. As a result, operations that rely on neighborhood information scale much worse for point clouds than for grid data, specially for large inputs and large neighborhoods. In this work, we address the scalability issue of point cloud methods by tackling its root cause: the irregularity of the data. We propose learnable gridification as the first step in a point cloud processing pipeline to transform the point cloud into a compact, regular grid. Thanks to gridification, subsequent layers can use operations defined on regular grids, e.g., Conv3D, which scale much better than native point cloud methods. We then extend gridification to point cloud to point cloud tasks, e.g., segmentation, by adding a learnable de-gridification step at the end of the point cloud processing pipeline to map the compact, regular grid back to its original point cloud form. Through theoretical and empirical analysis, we show that gridified networks scale better in terms of memory and time than networks directly applied on raw point cloud data, while being able to achieve competitive results. Our code is publicly available at https://github.com/computri/gridifier.

DNArch: Learning Convolutional Neural Architectures by Backpropagation

We present Differentiable Neural Architectures (DNArch), a method that jointly learns the weights and the architecture of Convolutional Neural Networks (CNNs) by backpropagation. In particular, DNArch allows learning (i) the size of convolutional kernels at each layer, (ii) the number of channels at each layer, (iii) the position and values of downsampling layers, and (iv) the depth of the network. To this end, DNArch views neural architectures as continuous multidimensional entities, and uses learnable differentiable masks along each dimension to control their size. Unlike existing methods, DNArch is not limited to a predefined set of possible neural components, but instead it is able to discover entire CNN architectures across all combinations of kernel sizes, widths, depths and downsampling. Empirically, DNArch finds performant CNN architectures for several classification and dense prediction tasks on both sequential and image data. When combined with a loss term that considers the network complexity, DNArch finds powerful architectures that respect a predefined computational budget.

Modelling Long Range Dependencies in N-D: From Task-Specific to a General Purpose CNN

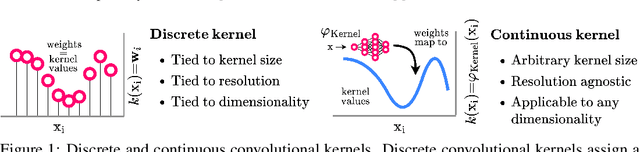
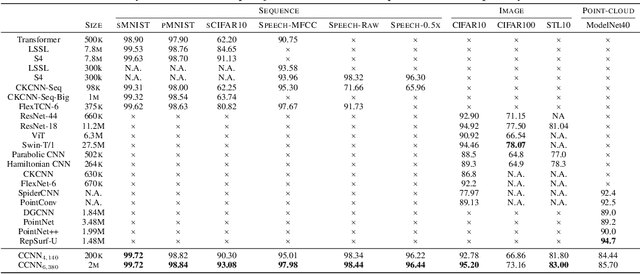
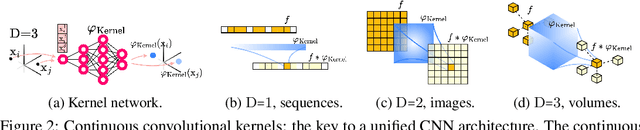
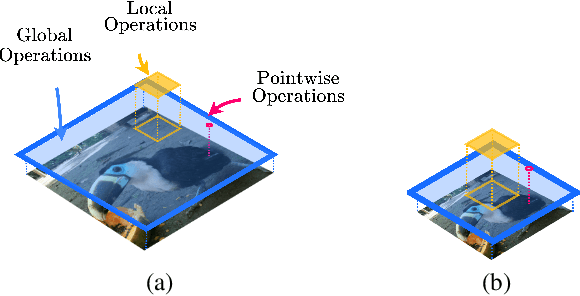
Performant Convolutional Neural Network (CNN) architectures must be tailored to specific tasks in order to consider the length, resolution, and dimensionality of the input data. In this work, we tackle the need for problem-specific CNN architectures. We present the Continuous Convolutional Neural Network (CCNN): a single CNN able to process data of arbitrary resolution, dimensionality and length without any structural changes. Its key component are its continuous convolutional kernels which model long-range dependencies at every layer, and thus remove the need of current CNN architectures for task-dependent downsampling and depths. We showcase the generality of our method by using the same architecture for tasks on sequential ($1{\rm D}$), visual ($2{\rm D}$) and point-cloud ($3{\rm D}$) data. Our CCNN matches and often outperforms the current state-of-the-art across all tasks considered.