A Free Lunch in LLM Compression: Revisiting Retraining after Pruning

While Neural Network pruning typically requires retraining the model to recover pruning-induced performance degradation, state-of-the-art Large Language Models (LLMs) pruning methods instead solve a layer-wise mask selection and reconstruction problem on a small set of calibration data to avoid full retraining, as it is considered computationally infeasible for LLMs. Reconstructing single matrices in isolation has favorable properties, such as convexity of the objective and significantly reduced memory requirements compared to full retraining. In practice, however, reconstruction is often implemented at coarser granularities, e.g., reconstructing a whole transformer block against its dense activations instead of a single matrix. In this work, we study the key design choices when reconstructing or retraining the remaining weights after pruning. We conduct an extensive computational study on state-of-the-art GPT architectures, and report several surprising findings that challenge common intuitions about retraining after pruning. In particular, we observe a free lunch scenario: reconstructing attention and MLP components separately within each transformer block is nearly the most resource-efficient yet achieves the best perplexity. Most importantly, this Pareto-optimal setup achieves better performance than full retraining, despite requiring only a fraction of the memory. Furthermore, we demonstrate that simple and efficient pruning criteria such as Wanda can outperform much more complex approaches when the reconstruction step is properly executed, highlighting its importance. Our findings challenge the narrative that retraining should be avoided at all costs and provide important insights into post-pruning performance recovery for LLMs.

Scalable DC Optimization via Adaptive Frank-Wolfe Algorithms

We consider the problem of minimizing a difference of (smooth) convex functions over a compact convex feasible region $P$, i.e., $\min_{x \in P} f(x) - g(x)$, with smooth $f$ and Lipschitz continuous $g$. This computational study builds upon and complements the framework of Maskan et al. [2025] by integrating advanced Frank-Wolfe variants to reduce computational overhead. We empirically show that constrained DC problems can be efficiently solved using a combination of the Blended Pairwise Conditional Gradients (BPCG) algorithm [Tsuji et al., 2022] with warm-starting and the adaptive error bound from Maskan et al. [2025]. The result is a highly efficient and scalable projection-free algorithm for constrained DC optimization.

Neural Concept Verifier: Scaling Prover-Verifier Games via Concept Encodings

While Prover-Verifier Games (PVGs) offer a promising path toward verifiability in nonlinear classification models, they have not yet been applied to complex inputs such as high-dimensional images. Conversely, Concept Bottleneck Models (CBMs) effectively translate such data into interpretable concepts but are limited by their reliance on low-capacity linear predictors. In this work, we introduce the Neural Concept Verifier (NCV), a unified framework combining PVGs with concept encodings for interpretable, nonlinear classification in high-dimensional settings. NCV achieves this by utilizing recent minimally supervised concept discovery models to extract structured concept encodings from raw inputs. A prover then selects a subset of these encodings, which a verifier -- implemented as a nonlinear predictor -- uses exclusively for decision-making. Our evaluations show that NCV outperforms CBM and pixel-based PVG classifier baselines on high-dimensional, logically complex datasets and also helps mitigate shortcut behavior. Overall, we demonstrate NCV as a promising step toward performative, verifiable AI.

Computational Algebra with Attention: Transformer Oracles for Border Basis Algorithms

Solving systems of polynomial equations, particularly those with finitely many solutions, is a crucial challenge across many scientific fields. Traditional methods like Gr\"obner and Border bases are fundamental but suffer from high computational costs, which have motivated recent Deep Learning approaches to improve efficiency, albeit at the expense of output correctness. In this work, we introduce the Oracle Border Basis Algorithm, the first Deep Learning approach that accelerates Border basis computation while maintaining output guarantees. To this end, we design and train a Transformer-based oracle that identifies and eliminates computationally expensive reduction steps, which we find to dominate the algorithm's runtime. By selectively invoking this oracle during critical phases of computation, we achieve substantial speedup factors of up to 3.5x compared to the base algorithm, without compromising the correctness of results. To generate the training data, we develop a sampling method and provide the first sampling theorem for border bases. We construct a tokenization and embedding scheme tailored to monomial-centered algebraic computations, resulting in a compact and expressive input representation, which reduces the number of tokens to encode an $n$-variate polynomial by a factor of $O(n)$. Our learning approach is data efficient, stable, and a practical enhancement to traditional computer algebra algorithms and symbolic computation.

Training on Plausible Counterfactuals Removes Spurious Correlations

Plausible counterfactual explanations (p-CFEs) are perturbations that minimally modify inputs to change classifier decisions while remaining plausible under the data distribution. In this study, we demonstrate that classifiers can be trained on p-CFEs labeled with induced \emph{incorrect} target classes to classify unperturbed inputs with the original labels. While previous studies have shown that such learning is possible with adversarial perturbations, we extend this paradigm to p-CFEs. Interestingly, our experiments reveal that learning from p-CFEs is even more effective: the resulting classifiers achieve not only high in-distribution accuracy but also exhibit significantly reduced bias with respect to spurious correlations.

RECON: Robust symmetry discovery via Explicit Canonical Orientation Normalization

Real-world data often exhibits unknown or approximate symmetries, yet existing equivariant networks must commit to a fixed transformation group prior to training, e.g., continuous $SO(2)$ rotations. This mismatch degrades performance when the actual data symmetries differ from those in the transformation group. We introduce RECON, a framework to discover each input's intrinsic symmetry distribution from unlabeled data. RECON leverages class-pose decompositions and applies a data-driven normalization to align arbitrary reference frames into a common natural pose, yielding directly comparable and interpretable symmetry descriptors. We demonstrate effective symmetry discovery on 2D image benchmarks and -- for the first time -- extend it to 3D transformation groups, paving the way towards more flexible equivariant modeling.

Linear Convergence of the Frank-Wolfe Algorithm over Product Polytopes

We study the linear convergence of Frank-Wolfe algorithms over product polytopes. We analyze two condition numbers for the product polytope, namely the \emph{pyramidal width} and the \emph{vertex-facet distance}, based on the condition numbers of individual polytope components. As a result, for convex objectives that are $\mu$-Polyak-{\L}ojasiewicz, we show linear convergence rates quantified in terms of the resulting condition numbers. We apply our results to the problem of approximately finding a feasible point in a polytope intersection in high-dimensions, and demonstrate the practical efficiency of our algorithms through empirical results.

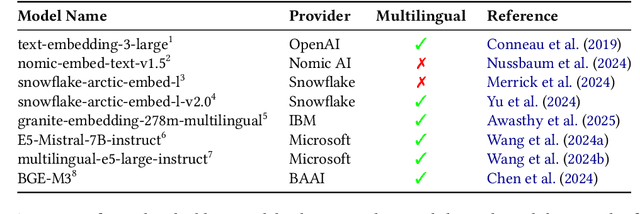
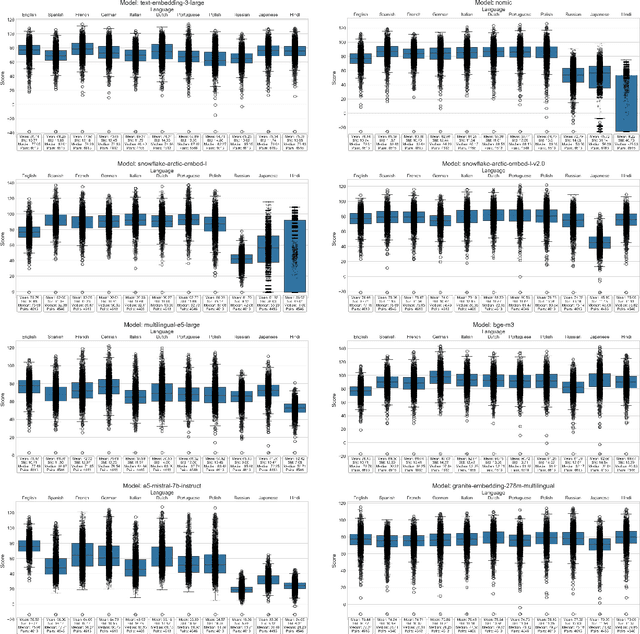
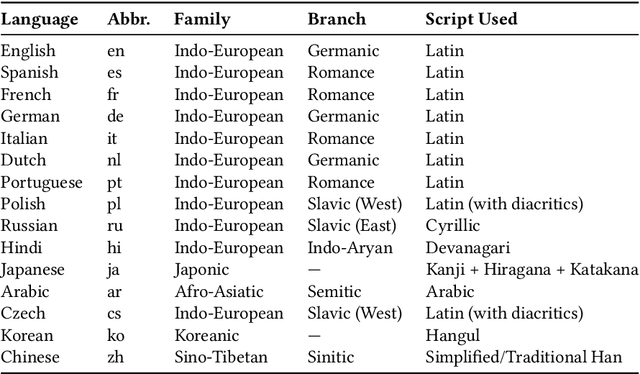
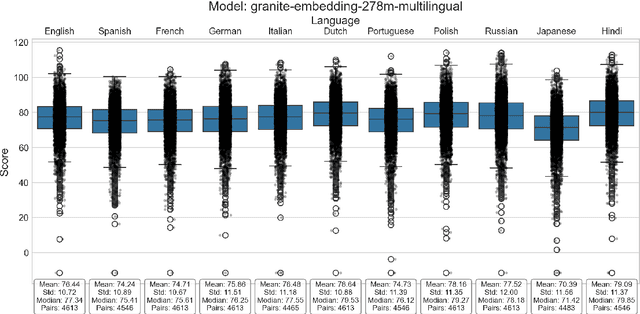
S-DAT: A Multilingual, GenAI-Driven Framework for Automated Divergent Thinking Assessment

This paper introduces S-DAT (Synthetic-Divergent Association Task), a scalable, multilingual framework for automated assessment of divergent thinking (DT) -a core component of human creativity. Traditional creativity assessments are often labor-intensive, language-specific, and reliant on subjective human ratings, limiting their scalability and cross-cultural applicability. In contrast, S-DAT leverages large language models and advanced multilingual embeddings to compute semantic distance -- a language-agnostic proxy for DT. We evaluate S-DAT across eleven diverse languages, including English, Spanish, German, Russian, Hindi, and Japanese (Kanji, Hiragana, Katakana), demonstrating robust and consistent scoring across linguistic contexts. Unlike prior DAT approaches, the S-DAT shows convergent validity with other DT measures and correct discriminant validity with convergent thinking. This cross-linguistic flexibility allows for more inclusive, global-scale creativity research, addressing key limitations of earlier approaches. S-DAT provides a powerful tool for fairer, more comprehensive evaluation of cognitive flexibility in diverse populations and can be freely assessed online: https://sdat.iol.zib.de/.

Sustainability via LLM Right-sizing

Large language models (LLMs) have become increasingly embedded in organizational workflows. This has raised concerns over their energy consumption, financial costs, and data sovereignty. While performance benchmarks often celebrate cutting-edge models, real-world deployment decisions require a broader perspective: when is a smaller, locally deployable model "good enough"? This study offers an empirical answer by evaluating eleven proprietary and open-weight LLMs across ten everyday occupational tasks, including summarizing texts, generating schedules, and drafting emails and proposals. Using a dual-LLM-based evaluation framework, we automated task execution and standardized evaluation across ten criteria related to output quality, factual accuracy, and ethical responsibility. Results show that GPT-4o delivers consistently superior performance but at a significantly higher cost and environmental footprint. Notably, smaller models like Gemma-3 and Phi-4 achieved strong and reliable results on most tasks, suggesting their viability in contexts requiring cost-efficiency, local deployment, or privacy. A cluster analysis revealed three model groups -- premium all-rounders, competent generalists, and limited but safe performers -- highlighting trade-offs between quality, control, and sustainability. Significantly, task type influenced model effectiveness: conceptual tasks challenged most models, while aggregation and transformation tasks yielded better performances. We argue for a shift from performance-maximizing benchmarks to task- and context-aware sufficiency assessments that better reflect organizational priorities. Our approach contributes a scalable method to evaluate AI models through a sustainability lens and offers actionable guidance for responsible LLM deployment in practice.

Approximating Latent Manifolds in Neural Networks via Vanishing Ideals

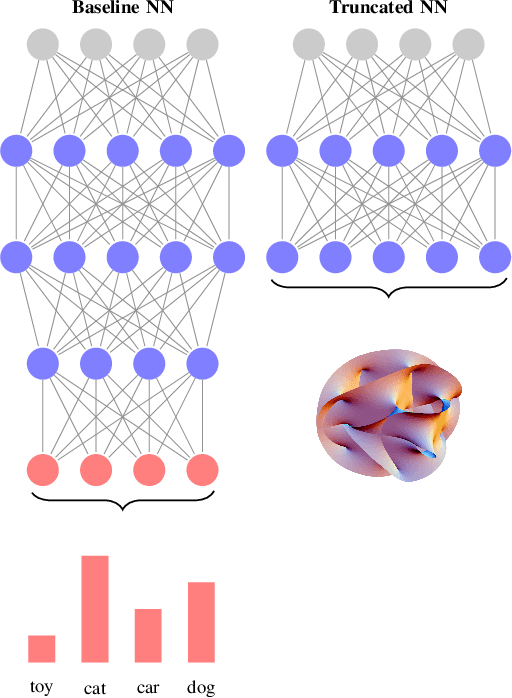
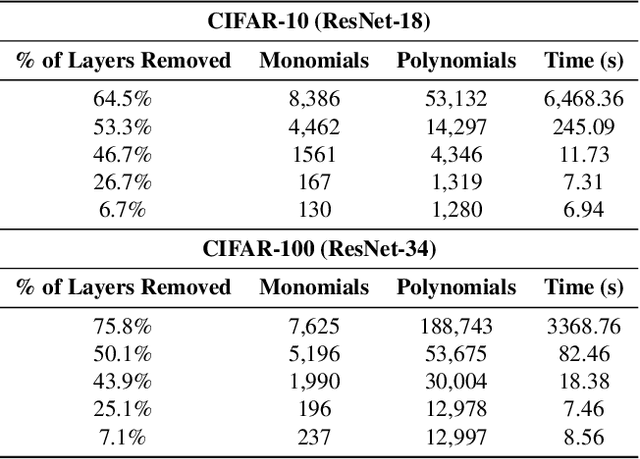
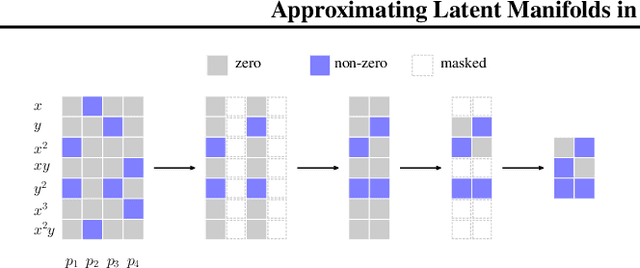
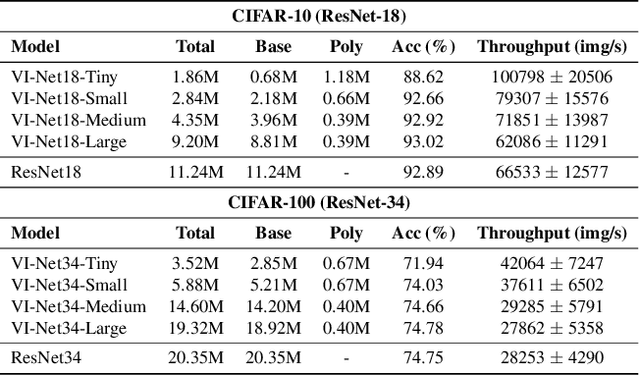
Deep neural networks have reshaped modern machine learning by learning powerful latent representations that often align with the manifold hypothesis: high-dimensional data lie on lower-dimensional manifolds. In this paper, we establish a connection between manifold learning and computational algebra by demonstrating how vanishing ideals can characterize the latent manifolds of deep networks. To that end, we propose a new neural architecture that (i) truncates a pretrained network at an intermediate layer, (ii) approximates each class manifold via polynomial generators of the vanishing ideal, and (iii) transforms the resulting latent space into linearly separable features through a single polynomial layer. The resulting models have significantly fewer layers than their pretrained baselines, while maintaining comparable accuracy, achieving higher throughput, and utilizing fewer parameters. Furthermore, drawing on spectral complexity analysis, we derive sharper theoretical guarantees for generalization, showing that our approach can in principle offer tighter bounds than standard deep networks. Numerical experiments confirm the effectiveness and efficiency of the proposed approach.