Navigating Shortcuts, Spurious Correlations, and Confounders: From Origins via Detection to Mitigation

Shortcuts, also described as Clever Hans behavior, spurious correlations, or confounders, present a significant challenge in machine learning and AI, critically affecting model generalization and robustness. Research in this area, however, remains fragmented across various terminologies, hindering the progress of the field as a whole. Consequently, we introduce a unifying taxonomy of shortcut learning by providing a formal definition of shortcuts and bridging the diverse terms used in the literature. In doing so, we further establish important connections between shortcuts and related fields, including bias, causality, and security, where parallels exist but are rarely discussed. Our taxonomy organizes existing approaches for shortcut detection and mitigation, providing a comprehensive overview of the current state of the field and revealing underexplored areas and open challenges. Moreover, we compile and classify datasets tailored to study shortcut learning. Altogether, this work provides a holistic perspective to deepen understanding and drive the development of more effective strategies for addressing shortcuts in machine learning.

Neural Concept Binder

The challenge in object-based visual reasoning lies in generating descriptive yet distinct concept representations. Moreover, doing this in an unsupervised fashion requires human users to understand a model's learned concepts and potentially revise false concepts. In addressing this challenge, we introduce the Neural Concept Binder, a new framework for deriving discrete concept representations resulting in what we term "concept-slot encodings". These encodings leverage both "soft binding" via object-centric block-slot encodings and "hard binding" via retrieval-based inference. The Neural Concept Binder facilitates straightforward concept inspection and direct integration of external knowledge, such as human input or insights from other AI models like GPT-4. Additionally, we demonstrate that incorporating the hard binding mechanism does not compromise performance; instead, it enables seamless integration into both neural and symbolic modules for intricate reasoning tasks, as evidenced by evaluations on our newly introduced CLEVR-Sudoku dataset.

Right on Time: Revising Time Series Models by Constraining their Explanations

The reliability of deep time series models is often compromised by their tendency to rely on confounding factors, which may lead to misleading results. Our newly recorded, naturally confounded dataset named P2S from a real mechanical production line emphasizes this. To tackle the challenging problem of mitigating confounders in time series data, we introduce Right on Time (RioT). Our method enables interactions with model explanations across both the time and frequency domain. Feedback on explanations in both domains is then used to constrain the model, steering it away from the annotated confounding factors. The dual-domain interaction strategy is crucial for effectively addressing confounders in time series datasets. We empirically demonstrate that RioT can effectively guide models away from the wrong reasons in P2S as well as popular time series classification and forecasting datasets.

United We Pretrain, Divided We Fail! Representation Learning for Time Series by Pretraining on 75 Datasets at Once

In natural language processing and vision, pretraining is utilized to learn effective representations. Unfortunately, the success of pretraining does not easily carry over to time series due to potential mismatch between sources and target. Actually, common belief is that multi-dataset pretraining does not work for time series! Au contraire, we introduce a new self-supervised contrastive pretraining approach to learn one encoding from many unlabeled and diverse time series datasets, so that the single learned representation can then be reused in several target domains for, say, classification. Specifically, we propose the XD-MixUp interpolation method and the Soft Interpolation Contextual Contrasting (SICC) loss. Empirically, this outperforms both supervised training and other self-supervised pretraining methods when finetuning on low-data regimes. This disproves the common belief: We can actually learn from multiple time series datasets, even from 75 at once.

Learning by Self-Explaining

Artificial intelligence (AI) research has a long track record of drawing inspirations from findings from biology, in particular human intelligence. In contrast to current AI research that mainly treats explanations as a means for model inspection, a somewhat neglected finding from human psychology is the benefit of self-explaining in an agents' learning process. Motivated by this, we introduce a novel learning paradigm, termed Learning by Self-Explaining (LSX). The underlying idea is that a learning module (learner) performs a base task, e.g. image classification, and provides explanations to its decisions. An internal critic module next evaluates the quality of these explanations given the original task. Finally, the learner is refined with the critic's feedback and the loop is repeated as required. The intuition behind this is that an explanation is considered "good" if the critic can perform the same task given the respective explanation. Despite many implementation possibilities the structure of any LSX instantiation can be taxonomized based on four learning modules which we identify as: Fit, Explain, Reflect and Revise. In our work, we provide distinct instantiations of LSX for two different learner models, each illustrating different choices for the various LSX components. We broadly evaluate these on several datasets and show that Learning by Self-Explaining not only boosts the generalization abilities of AI models, particularly in small-data regimes, but also aids in mitigating the influence of confounding factors, as well as leading to more task specific and faithful model explanations. Overall, our results provide experimental evidence of the potential of self-explaining within the learning phase of an AI model.

Learning to Intervene on Concept Bottlenecks

While traditional deep learning models often lack interpretability, concept bottleneck models (CBMs) provide inherent explanations via their concept representations. Specifically, they allow users to perform interventional interactions on these concepts by updating the concept values and thus correcting the predictive output of the model. Traditionally, however, these interventions are applied to the model only once and discarded afterward. To rectify this, we present concept bottleneck memory models (CB2M), an extension to CBMs. Specifically, a CB2M learns to generalize interventions to appropriate novel situations via a two-fold memory with which it can learn to detect mistakes and to reapply previous interventions. In this way, a CB2M learns to automatically improve model performance from a few initially obtained interventions. If no prior human interventions are available, a CB2M can detect potential mistakes of the CBM bottleneck and request targeted interventions. In our experimental evaluations on challenging scenarios like handling distribution shifts and confounded training data, we illustrate that CB2M are able to successfully generalize interventions to unseen data and can indeed identify wrongly inferred concepts. Overall, our results show that CB2M is a great tool for users to provide interactive feedback on CBMs, e.g., by guiding a user's interaction and requiring fewer interventions.

One Explanation Does Not Fit XIL

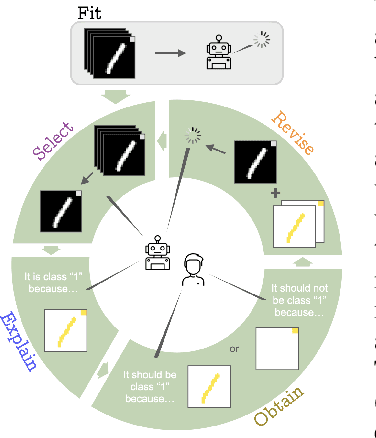
Current machine learning models produce outstanding results in many areas but, at the same time, suffer from shortcut learning and spurious correlations. To address such flaws, the explanatory interactive machine learning (XIL) framework has been proposed to revise a model by employing user feedback on a model's explanation. This work sheds light on the explanations used within this framework. In particular, we investigate simultaneous model revision through multiple explanation methods. To this end, we identified that \textit{one explanation does not fit XIL} and propose considering multiple ones when revising models via XIL.

Machines Explaining Linear Programs

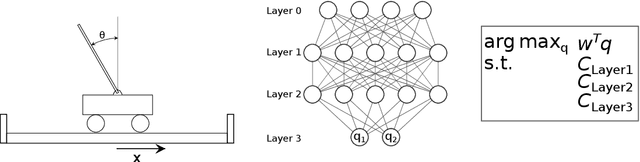
There has been a recent push in making machine learning models more interpretable so that their performance can be trusted. Although successful, these methods have mostly focused on the deep learning methods while the fundamental optimization methods in machine learning such as linear programs (LP) have been left out. Even if LPs can be considered as whitebox or clearbox models, they are not easy to understand in terms of relationships between inputs and outputs. As a linear program only provides the optimal solution to an optimization problem, further explanations are often helpful. In this work, we extend the attribution methods for explaining neural networks to linear programs. These methods explain the model by providing relevance scores for the model inputs, to show the influence of each input on the output. Alongside using classical gradient-based attribution methods we also propose a way to adapt perturbation-based attribution methods to LPs. Our evaluations of several different linear and integer problems showed that attribution methods can generate useful explanations for linear programs. However, we also demonstrate that using a neural attribution method directly might come with some drawbacks, as the properties of these methods on neural networks do not necessarily transfer to linear programs. The methods can also struggle if a linear program has more than one optimal solution, as a solver just returns one possible solution. Our results can hopefully be used as a good starting point for further research in this direction.