DUNIA: Pixel-Sized Embeddings via Cross-Modal Alignment for Earth Observation Applications

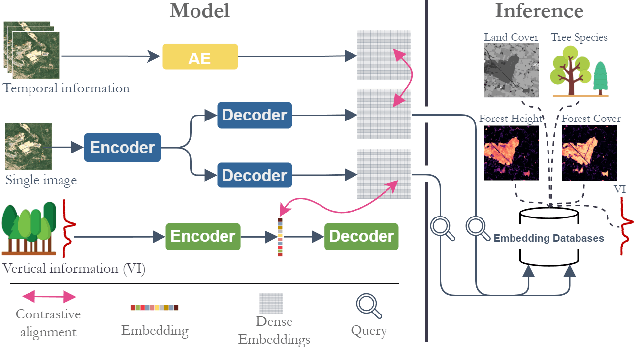
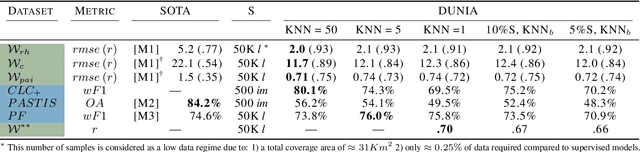
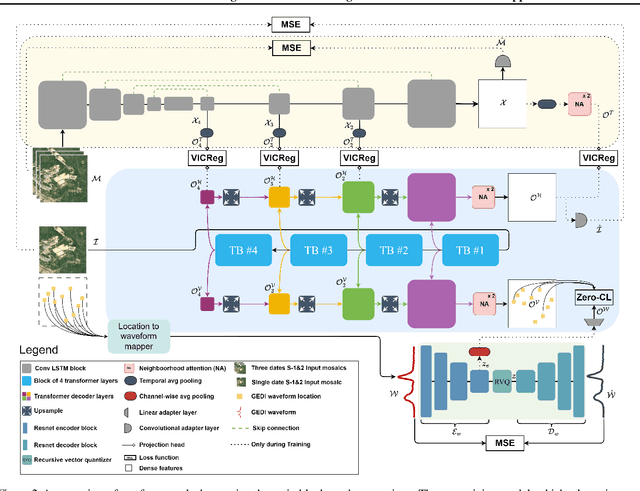
Significant efforts have been directed towards adapting self-supervised multimodal learning for Earth observation applications. However, existing methods produce coarse patch-sized embeddings, limiting their effectiveness and integration with other modalities like LiDAR. To close this gap, we present DUNIA, an approach to learn pixel-sized embeddings through cross-modal alignment between images and full-waveform LiDAR data. As the model is trained in a contrastive manner, the embeddings can be directly leveraged in the context of a variety of environmental monitoring tasks in a zero-shot setting. In our experiments, we demonstrate the effectiveness of the embeddings for seven such tasks (canopy height mapping, fractional canopy cover, land cover mapping, tree species identification, plant area index, crop type classification, and per-pixel waveform-based vertical structure mapping). The results show that the embeddings, along with zero-shot classifiers, often outperform specialized supervised models, even in low data regimes. In the fine-tuning setting, we show strong low-shot capabilities with performances near or better than state-of-the-art on five out of six tasks.

Approximating Latent Manifolds in Neural Networks via Vanishing Ideals

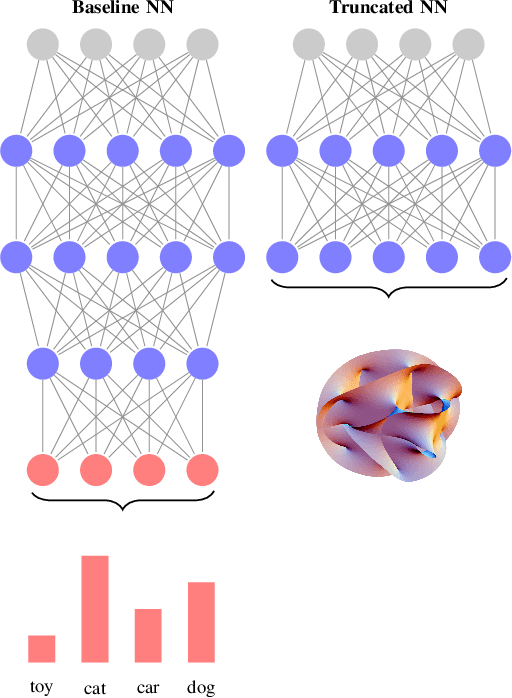
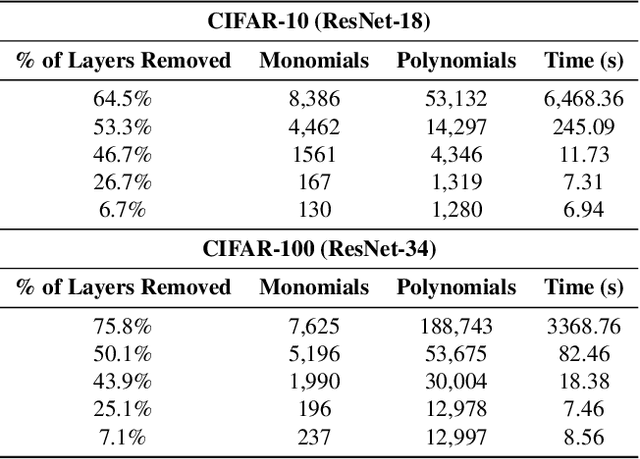
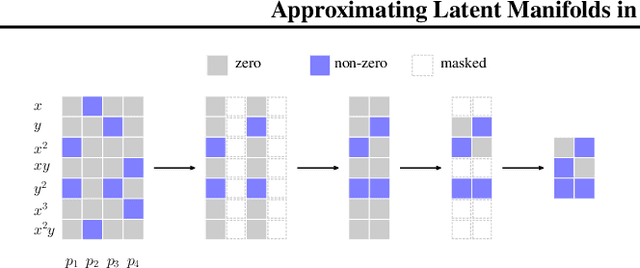
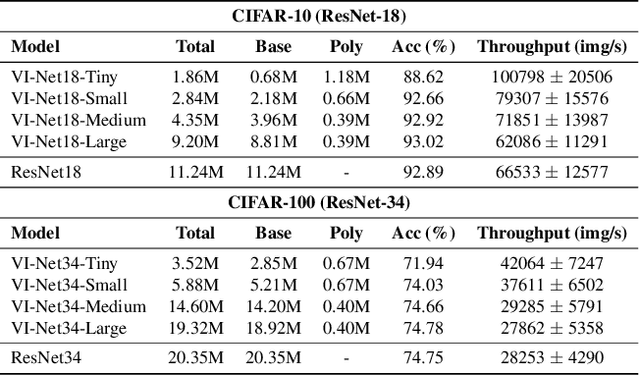
Deep neural networks have reshaped modern machine learning by learning powerful latent representations that often align with the manifold hypothesis: high-dimensional data lie on lower-dimensional manifolds. In this paper, we establish a connection between manifold learning and computational algebra by demonstrating how vanishing ideals can characterize the latent manifolds of deep networks. To that end, we propose a new neural architecture that (i) truncates a pretrained network at an intermediate layer, (ii) approximates each class manifold via polynomial generators of the vanishing ideal, and (iii) transforms the resulting latent space into linearly separable features through a single polynomial layer. The resulting models have significantly fewer layers than their pretrained baselines, while maintaining comparable accuracy, achieving higher throughput, and utilizing fewer parameters. Furthermore, drawing on spectral complexity analysis, we derive sharper theoretical guarantees for generalization, showing that our approach can in principle offer tighter bounds than standard deep networks. Numerical experiments confirm the effectiveness and efficiency of the proposed approach.

Capturing Temporal Dynamics in Large-Scale Canopy Tree Height Estimation

With the rise in global greenhouse gas emissions, accurate large-scale tree canopy height maps are essential for understanding forest structure, estimating above-ground biomass, and monitoring ecological disruptions. To this end, we present a novel approach to generate large-scale, high-resolution canopy height maps over time. Our model accurately predicts canopy height over multiple years given Sentinel-2 time series satellite data. Using GEDI LiDAR data as the ground truth for training the model, we present the first 10m resolution temporal canopy height map of the European continent for the period 2019-2022. As part of this product, we also offer a detailed canopy height map for 2020, providing more precise estimates than previous studies. Our pipeline and the resulting temporal height map are publicly available, enabling comprehensive large-scale monitoring of forests and, hence, facilitating future research and ecological analyses. For an interactive viewer, see https://europetreemap.projects.earthengine.app/view/temporalcanopyheight.

Neural Discovery in Mathematics: Do Machines Dream of Colored Planes?

We demonstrate how neural networks can drive mathematical discovery through a case study of the Hadwiger-Nelson problem, a long-standing open problem from discrete geometry and combinatorics about coloring the plane avoiding monochromatic unit-distance pairs. Using neural networks as approximators, we reformulate this mixed discrete-continuous geometric coloring problem as an optimization task with a probabilistic, differentiable loss function. This enables gradient-based exploration of admissible configurations that most significantly led to the discovery of two novel six-colorings, providing the first improvements in thirty years to the off-diagonal variant of the original problem (Mundinger et al., 2024a). Here, we establish the underlying machine learning approach used to obtain these results and demonstrate its broader applicability through additional results and numerical insights.

Estimating Canopy Height at Scale

We propose a framework for global-scale canopy height estimation based on satellite data. Our model leverages advanced data preprocessing techniques, resorts to a novel loss function designed to counter geolocation inaccuracies inherent in the ground-truth height measurements, and employs data from the Shuttle Radar Topography Mission to effectively filter out erroneous labels in mountainous regions, enhancing the reliability of our predictions in those areas. A comparison between predictions and ground-truth labels yields an MAE / RMSE of 2.43 / 4.73 (meters) overall and 4.45 / 6.72 (meters) for trees taller than five meters, which depicts a substantial improvement compared to existing global-scale maps. The resulting height map as well as the underlying framework will facilitate and enhance ecological analyses at a global scale, including, but not limited to, large-scale forest and biomass monitoring.

Neural Parameter Regression for Explicit Representations of PDE Solution Operators

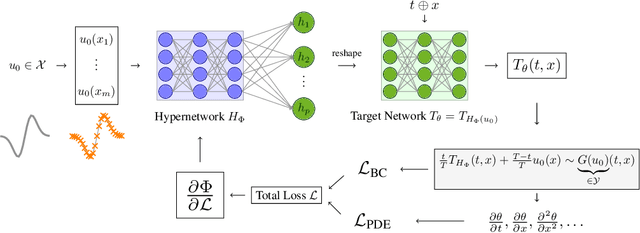
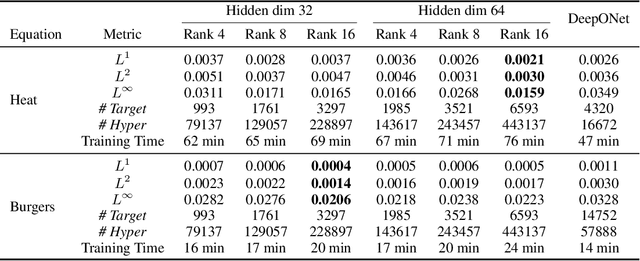
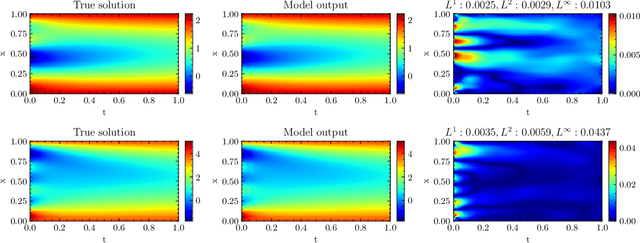
We introduce Neural Parameter Regression (NPR), a novel framework specifically developed for learning solution operators in Partial Differential Equations (PDEs). Tailored for operator learning, this approach surpasses traditional DeepONets (Lu et al., 2021) by employing Physics-Informed Neural Network (PINN, Raissi et al., 2019) techniques to regress Neural Network (NN) parameters. By parametrizing each solution based on specific initial conditions, it effectively approximates a mapping between function spaces. Our method enhances parameter efficiency by incorporating low-rank matrices, thereby boosting computational efficiency and scalability. The framework shows remarkable adaptability to new initial and boundary conditions, allowing for rapid fine-tuning and inference, even in cases of out-of-distribution examples.

On the Byzantine-Resilience of Distillation-Based Federated Learning

Federated Learning (FL) algorithms using Knowledge Distillation (KD) have received increasing attention due to their favorable properties with respect to privacy, non-i.i.d. data and communication cost. These methods depart from transmitting model parameters and, instead, communicate information about a learning task by sharing predictions on a public dataset. In this work, we study the performance of such approaches in the byzantine setting, where a subset of the clients act in an adversarial manner aiming to disrupt the learning process. We show that KD-based FL algorithms are remarkably resilient and analyze how byzantine clients can influence the learning process compared to Federated Averaging. Based on these insights, we introduce two new byzantine attacks and demonstrate that they are effective against prior byzantine-resilient methods. Additionally, we propose FilterExp, a novel method designed to enhance the byzantine resilience of KD-based FL algorithms and demonstrate its efficacy. Finally, we provide a general method to make attacks harder to detect, improving their effectiveness.

PERP: Rethinking the Prune-Retrain Paradigm in the Era of LLMs

Neural Networks can be efficiently compressed through pruning, significantly reducing storage and computational demands while maintaining predictive performance. Simple yet effective methods like Iterative Magnitude Pruning (IMP, Han et al., 2015) remove less important parameters and require a costly retraining procedure to recover performance after pruning. However, with the rise of Large Language Models (LLMs), full retraining has become infeasible due to memory and compute constraints. In this study, we challenge the practice of retraining all parameters by demonstrating that updating only a small subset of highly expressive parameters is often sufficient to recover or even improve performance compared to full retraining. Surprisingly, retraining as little as 0.27%-0.35% of the parameters of GPT-architectures (OPT-2.7B/6.7B/13B/30B) achieves comparable performance to One Shot IMP across various sparsity levels. Our method, Parameter-Efficient Retraining after Pruning (PERP), drastically reduces compute and memory demands, enabling pruning and retraining of up to 30 billion parameter models on a single NVIDIA A100 GPU within minutes. Despite magnitude pruning being considered as unsuited for pruning LLMs, our findings show that PERP positions it as a strong contender against state-of-the-art retraining-free approaches such as Wanda (Sun et al., 2023) and SparseGPT (Frantar & Alistarh, 2023), opening up a promising alternative to avoiding retraining.

Sparse Model Soups: A Recipe for Improved Pruning via Model Averaging

Neural networks can be significantly compressed by pruning, leading to sparse models requiring considerably less storage and floating-point operations while maintaining predictive performance. Model soups (Wortsman et al., 2022) improve generalization and out-of-distribution performance by averaging the parameters of multiple models into a single one without increased inference time. However, identifying models in the same loss basin to leverage both sparsity and parameter averaging is challenging, as averaging arbitrary sparse models reduces the overall sparsity due to differing sparse connectivities. In this work, we address these challenges by demonstrating that exploring a single retraining phase of Iterative Magnitude Pruning (IMP) with varying hyperparameter configurations, such as batch ordering or weight decay, produces models that are suitable for averaging and share the same sparse connectivity by design. Averaging these models significantly enhances generalization performance compared to their individual components. Building on this idea, we introduce Sparse Model Soups (SMS), a novel method for merging sparse models by initiating each prune-retrain cycle with the averaged model of the previous phase. SMS maintains sparsity, exploits sparse network benefits being modular and fully parallelizable, and substantially improves IMP's performance. Additionally, we demonstrate that SMS can be adapted to enhance the performance of state-of-the-art pruning during training approaches.

Merlin-Arthur Classifiers: Formal Interpretability with Interactive Black Boxes

We present a new theoretical framework for making black box classifiers such as Neural Networks interpretable, basing our work on clear assumptions and guarantees. In our setting, which is inspired by the Merlin-Arthur protocol from Interactive Proof Systems, two functions cooperate to achieve a classification together: the \emph{prover} selects a small set of features as a certificate and presents it to the \emph{classifier}. Including a second, adversarial prover allows us to connect a game-theoretic equilibrium to information-theoretic guarantees on the exchanged features. We define notions of completeness and soundness that enable us to lower bound the mutual information between features and class. To demonstrate good agreement between theory and practice, we support our framework by providing numerical experiments for Neural Network classifiers, explicitly calculating the mutual information of features with respect to the class.