Fighting MRI Anisotropy: Learning Multiple Cardiac Shapes From a Single Implicit Neural Representation

The anisotropic nature of short-axis (SAX) cardiovascular magnetic resonance imaging (CMRI) limits cardiac shape analysis. To address this, we propose to leverage near-isotropic, higher resolution computed tomography angiography (CTA) data of the heart. We use this data to train a single neural implicit function to jointly represent cardiac shapes from CMRI at any resolution. We evaluate the method for the reconstruction of right ventricle (RV) and myocardium (MYO), where MYO simultaneously models endocardial and epicardial left-ventricle surfaces. Since high-resolution SAX reference segmentations are unavailable, we evaluate performance by extracting a 4-chamber (4CH) slice of RV and MYO from their reconstructed shapes. When compared with the reference 4CH segmentation masks from CMRI, our method achieved a Dice similarity coefficient of 0.91 $\pm$ 0.07 and 0.75 $\pm$ 0.13, and a Hausdorff distance of 6.21 $\pm$ 3.97 mm and 7.53 $\pm$ 5.13 mm for RV and MYO, respectively. Quantitative and qualitative assessment demonstrate the model's ability to reconstruct accurate, smooth and anatomically plausible shapes, supporting improvements in cardiac shape analysis.

Learning Symmetries via Weight-Sharing with Doubly Stochastic Tensors

Group equivariance has emerged as a valuable inductive bias in deep learning, enhancing generalization, data efficiency, and robustness. Classically, group equivariant methods require the groups of interest to be known beforehand, which may not be realistic for real-world data. Additionally, baking in fixed group equivariance may impose overly restrictive constraints on model architecture. This highlights the need for methods that can dynamically discover and apply symmetries as soft constraints. For neural network architectures, equivariance is commonly achieved through group transformations of a canonical weight tensor, resulting in weight sharing over a given group $G$. In this work, we propose to learn such a weight-sharing scheme by defining a collection of learnable doubly stochastic matrices that act as soft permutation matrices on canonical weight tensors, which can take regular group representations as a special case. This yields learnable kernel transformations that are jointly optimized with downstream tasks. We show that when the dataset exhibits strong symmetries, the permutation matrices will converge to regular group representations and our weight-sharing networks effectively become regular group convolutions. Additionally, the flexibility of the method enables it to effectively pick up on partial symmetries.

Regular SE(3) Group Convolutions for Volumetric Medical Image Analysis

Regular group convolutional neural networks (G-CNNs) have been shown to increase model performance and improve equivariance to different geometrical symmetries. This work addresses the problem of SE(3), i.e., roto-translation equivariance, on volumetric data. Volumetric image data is prevalent in many medical settings. Motivated by the recent work on separable group convolutions, we devise a SE(3) group convolution kernel separated into a continuous SO(3) (rotation) kernel and a spatial kernel. We approximate equivariance to the continuous setting by sampling uniform SO(3) grids. Our continuous SO(3) kernel is parameterized via RBF interpolation on similarly uniform grids. We demonstrate the advantages of our approach in volumetric medical image analysis. Our SE(3) equivariant models consistently outperform CNNs and regular discrete G-CNNs on challenging medical classification tasks and show significantly improved generalization capabilities. Our approach achieves up to a 16.5% gain in accuracy over regular CNNs.

Hard Occlusions in Visual Object Tracking

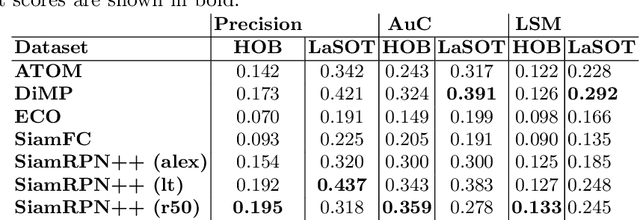
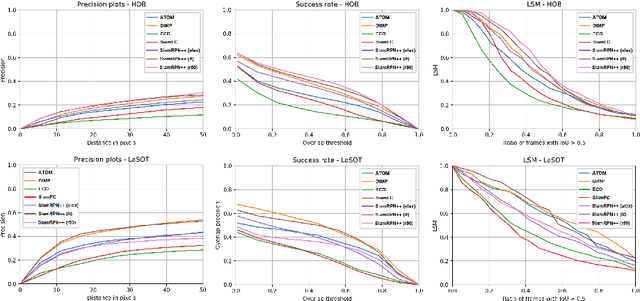
Visual object tracking is among the hardest problems in computer vision, as trackers have to deal with many challenging circumstances such as illumination changes, fast motion, occlusion, among others. A tracker is assessed to be good or not based on its performance on the recent tracking datasets, e.g., VOT2019, and LaSOT. We argue that while the recent datasets contain large sets of annotated videos that to some extent provide a large bandwidth for training data, the hard scenarios such as occlusion and in-plane rotation are still underrepresented. For trackers to be brought closer to the real-world scenarios and deployed in safety-critical devices, even the rarest hard scenarios must be properly addressed. In this paper, we particularly focus on hard occlusion cases and benchmark the performance of recent state-of-the-art trackers (SOTA) on them. We created a small-scale dataset containing different categories within hard occlusions, on which the selected trackers are evaluated. Results show that hard occlusions remain a very challenging problem for SOTA trackers. Furthermore, it is observed that tracker performance varies wildly between different categories of hard occlusions, where a top-performing tracker on one category performs significantly worse on a different category. The varying nature of tracker performance based on specific categories suggests that the common tracker rankings using averaged single performance scores are not adequate to gauge tracker performance in real-world scenarios.