Towards Variational Flow Matching on General Geometries
Paper and Code
Feb 18, 2025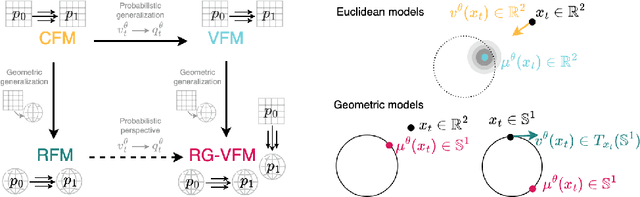


We introduce Riemannian Gaussian Variational Flow Matching (RG-VFM), an extension of Variational Flow Matching (VFM) that leverages Riemannian Gaussian distributions for generative modeling on structured manifolds. We derive a variational objective for probability flows on manifolds with closed-form geodesics, making RG-VFM comparable - though fundamentally different to Riemannian Flow Matching (RFM) in this geometric setting. Experiments on a checkerboard dataset wrapped on the sphere demonstrate that RG-VFM captures geometric structure more effectively than Euclidean VFM and baseline methods, establishing it as a robust framework for manifold-aware generative modeling.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge