Olga Zaghen
Towards Variational Flow Matching on General Geometries
Feb 18, 2025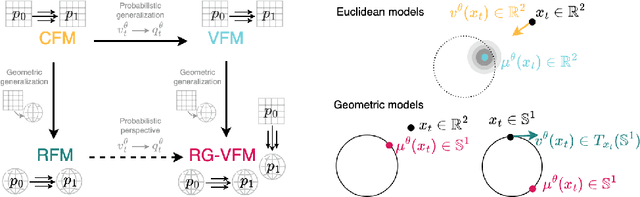


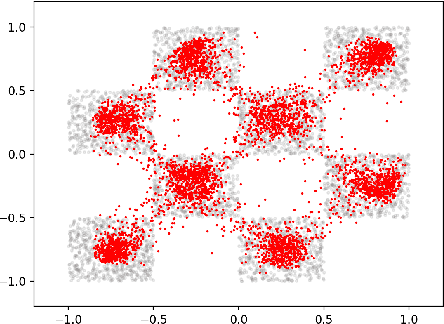
Abstract:We introduce Riemannian Gaussian Variational Flow Matching (RG-VFM), an extension of Variational Flow Matching (VFM) that leverages Riemannian Gaussian distributions for generative modeling on structured manifolds. We derive a variational objective for probability flows on manifolds with closed-form geodesics, making RG-VFM comparable - though fundamentally different to Riemannian Flow Matching (RFM) in this geometric setting. Experiments on a checkerboard dataset wrapped on the sphere demonstrate that RG-VFM captures geometric structure more effectively than Euclidean VFM and baseline methods, establishing it as a robust framework for manifold-aware generative modeling.
ICML Topological Deep Learning Challenge 2024: Beyond the Graph Domain
Sep 08, 2024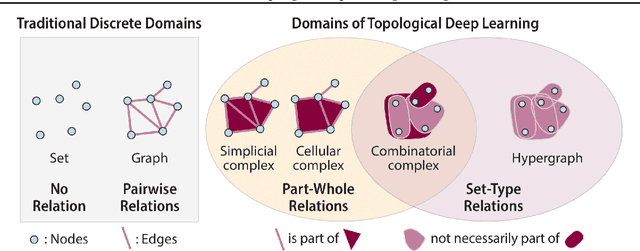
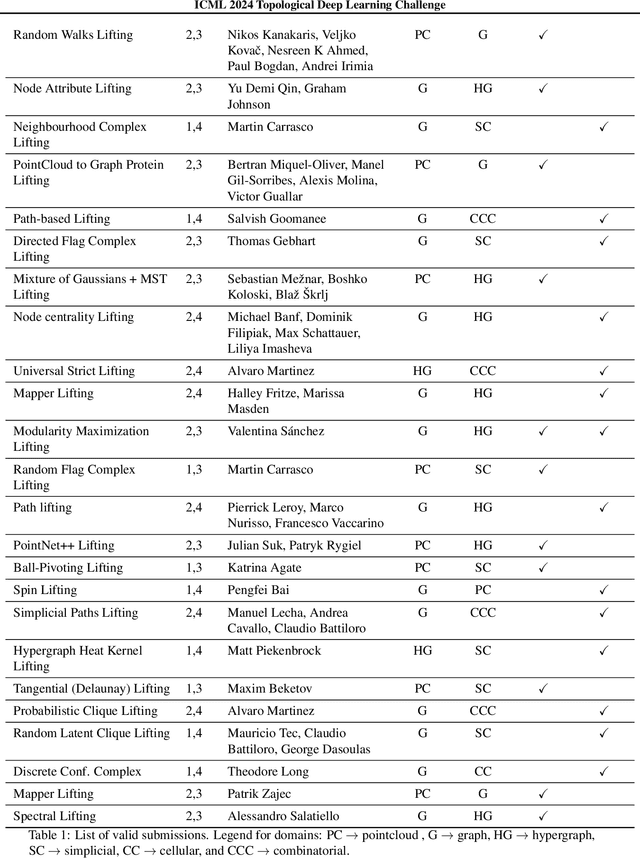
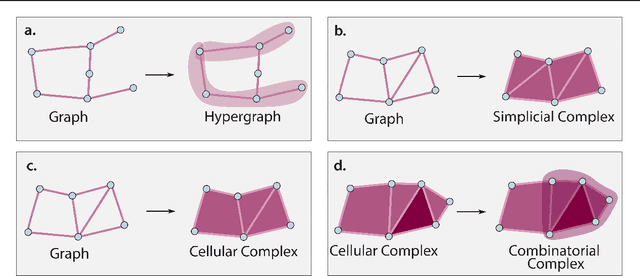
Abstract:This paper describes the 2nd edition of the ICML Topological Deep Learning Challenge that was hosted within the ICML 2024 ELLIS Workshop on Geometry-grounded Representation Learning and Generative Modeling (GRaM). The challenge focused on the problem of representing data in different discrete topological domains in order to bridge the gap between Topological Deep Learning (TDL) and other types of structured datasets (e.g. point clouds, graphs). Specifically, participants were asked to design and implement topological liftings, i.e. mappings between different data structures and topological domains --like hypergraphs, or simplicial/cell/combinatorial complexes. The challenge received 52 submissions satisfying all the requirements. This paper introduces the main scope of the challenge, and summarizes the main results and findings.
Revisiting Random Walks for Learning on Graphs
Jul 01, 2024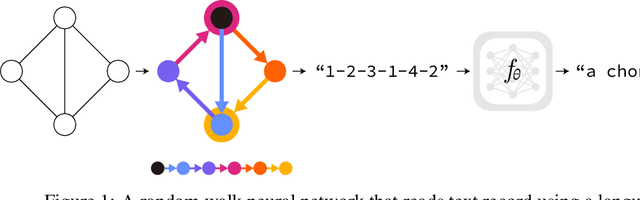
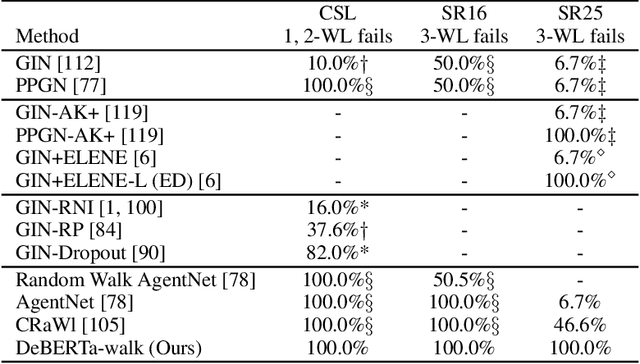
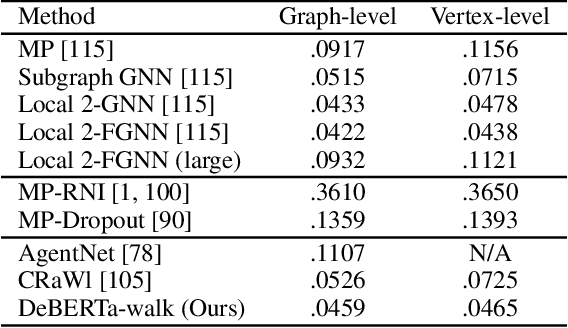
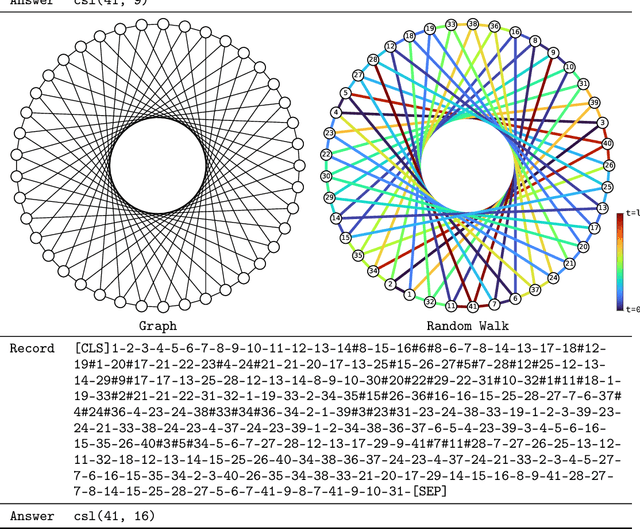
Abstract:We revisit a simple idea for machine learning on graphs, where a random walk on a graph produces a machine-readable record, and this record is processed by a deep neural network to directly make vertex-level or graph-level predictions. We refer to these stochastic machines as random walk neural networks, and show that we can design them to be isomorphism invariant while capable of universal approximation of graph functions in probability. A useful finding is that almost any kind of record of random walk guarantees probabilistic invariance as long as the vertices are anonymized. This enables us to record random walks in plain text and adopt a language model to read these text records to solve graph tasks. We further establish a parallelism to message passing neural networks using tools from Markov chain theory, and show that over-smoothing in message passing is alleviated by construction in random walk neural networks, while over-squashing manifests as probabilistic under-reaching. We show that random walk neural networks based on pre-trained language models can solve several hard problems on graphs, such as separating strongly regular graphs where the 3-WL test fails, counting substructures, and transductive classification on arXiv citation network without training. Code is available at https://github.com/jw9730/random-walk.
Nonlinear Sheaf Diffusion in Graph Neural Networks
Mar 01, 2024
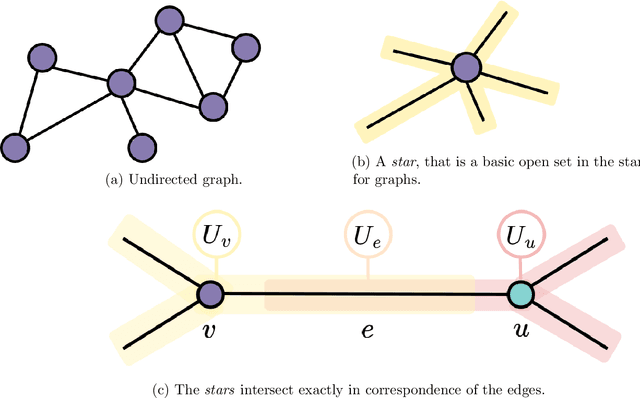
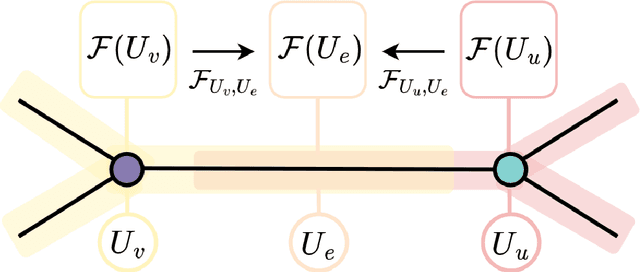
Abstract:This work focuses on exploring the potential benefits of introducing a nonlinear Laplacian in Sheaf Neural Networks for graph-related tasks. The primary aim is to understand the impact of such nonlinearity on diffusion dynamics, signal propagation, and performance of neural network architectures in discrete-time settings. The study primarily emphasizes experimental analysis, using real-world and synthetic datasets to validate the practical effectiveness of different versions of the model. This approach shifts the focus from an initial theoretical exploration to demonstrating the practical utility of the proposed model.
TopoX: A Suite of Python Packages for Machine Learning on Topological Domains
Feb 07, 2024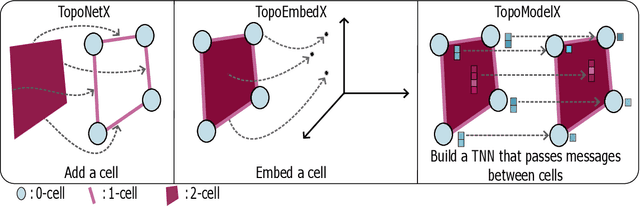
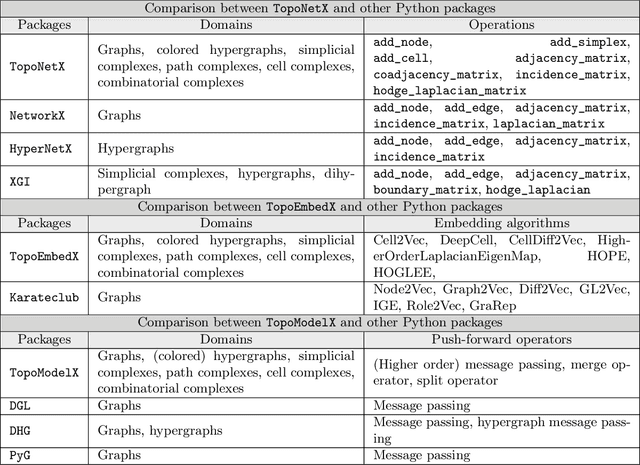
Abstract:We introduce topox, a Python software suite that provides reliable and user-friendly building blocks for computing and machine learning on topological domains that extend graphs: hypergraphs, simplicial, cellular, path and combinatorial complexes. topox consists of three packages: toponetx facilitates constructing and computing on these domains, including working with nodes, edges and higher-order cells; topoembedx provides methods to embed topological domains into vector spaces, akin to popular graph-based embedding algorithms such as node2vec; topomodelx is built on top of PyTorch and offers a comprehensive toolbox of higher-order message passing functions for neural networks on topological domains. The extensively documented and unit-tested source code of topox is available under MIT license at https://github.com/pyt-team.
Hypergraph Neural Networks through the Lens of Message Passing: A Common Perspective to Homophily and Architecture Design
Oct 11, 2023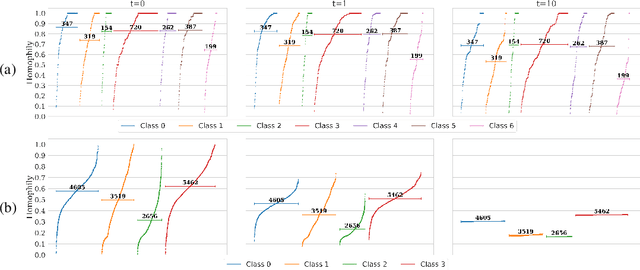
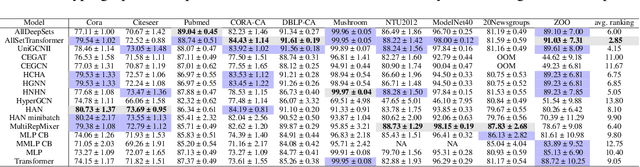

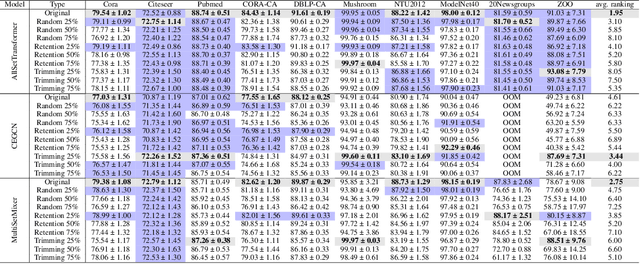
Abstract:Most of the current hypergraph learning methodologies and benchmarking datasets in the hypergraph realm are obtained by lifting procedures from their graph analogs, simultaneously leading to overshadowing hypergraph network foundations. This paper attempts to confront some pending questions in that regard: Can the concept of homophily play a crucial role in Hypergraph Neural Networks (HGNNs), similar to its significance in graph-based research? Is there room for improving current hypergraph architectures and methodologies? (e.g. by carefully addressing the specific characteristics of higher-order networks) Do existing datasets provide a meaningful benchmark for HGNNs? Diving into the details, this paper proposes a novel conceptualization of homophily in higher-order networks based on a message passing scheme; this approach harmonizes the analytical frameworks of datasets and architectures, offering a unified perspective for exploring and interpreting complex, higher-order network structures and dynamics. Further, we propose MultiSet, a novel message passing framework that redefines HGNNs by allowing hyperedge-dependent node representations, as well as introduce a novel architecture MultiSetMixer that leverages a new hyperedge sampling strategy. Finally, we provide an extensive set of experiments that contextualize our proposals and lead to valuable insights in hypergraph representation learning.
ICML 2023 Topological Deep Learning Challenge : Design and Results
Oct 02, 2023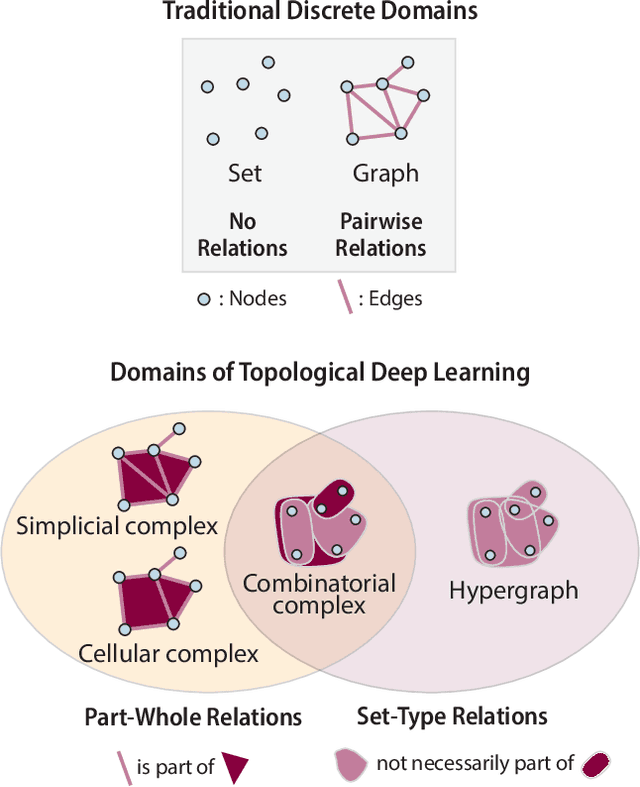
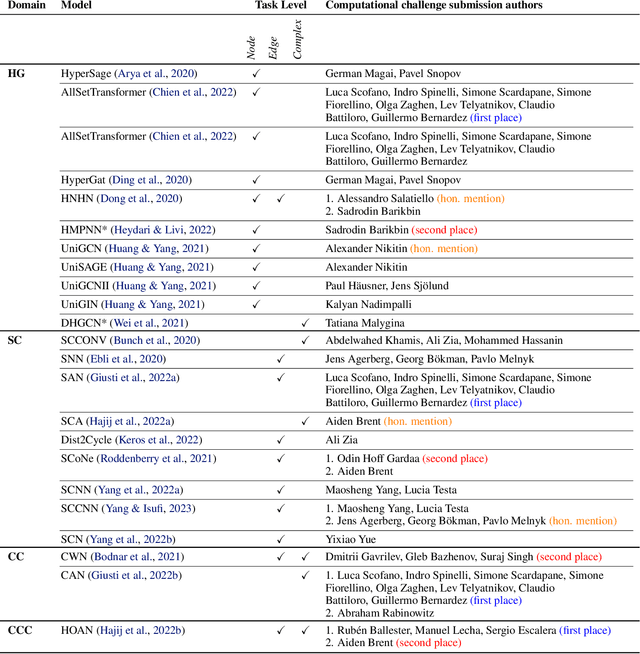
Abstract:This paper presents the computational challenge on topological deep learning that was hosted within the ICML 2023 Workshop on Topology and Geometry in Machine Learning. The competition asked participants to provide open-source implementations of topological neural networks from the literature by contributing to the python packages TopoNetX (data processing) and TopoModelX (deep learning). The challenge attracted twenty-eight qualifying submissions in its two-month duration. This paper describes the design of the challenge and summarizes its main findings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge