Can Neural Networks Learn Small Algebraic Worlds? An Investigation Into the Group-theoretic Structures Learned By Narrow Models Trained To Predict Group Operations

While a real-world research program in mathematics may be guided by a motivating question, the process of mathematical discovery is typically open-ended. Ideally, exploration needed to answer the original question will reveal new structures, patterns, and insights that are valuable in their own right. This contrasts with the exam-style paradigm in which the machine learning community typically applies AI to math. To maximize progress in mathematics using AI, we will need to go beyond simple question answering. With this in mind, we explore the extent to which narrow models trained to solve a fixed mathematical task learn broader mathematical structure that can be extracted by a researcher or other AI system. As a basic test case for this, we use the task of training a neural network to predict a group operation (for example, performing modular arithmetic or composition of permutations). We describe a suite of tests designed to assess whether the model captures significant group-theoretic notions such as the identity element, commutativity, or subgroups. Through extensive experimentation we find evidence that models learn representations capable of capturing abstract algebraic properties. For example, we find hints that models capture the commutativity of modular arithmetic. We are also able to train linear classifiers that reliably distinguish between elements of certain subgroups (even though no labels for these subgroups are included in the data). On the other hand, we are unable to extract notions such as the concept of the identity element. Together, our results suggest that in some cases the representations of even small neural networks can be used to distill interesting abstract structure from new mathematical objects.

Machine Learning meets Algebraic Combinatorics: A Suite of Datasets Capturing Research-level Conjecturing Ability in Pure Mathematics

With recent dramatic increases in AI system capabilities, there has been growing interest in utilizing machine learning for reasoning-heavy, quantitative tasks, particularly mathematics. While there are many resources capturing mathematics at the high-school, undergraduate, and graduate level, there are far fewer resources available that align with the level of difficulty and open endedness encountered by professional mathematicians working on open problems. To address this, we introduce a new collection of datasets, the Algebraic Combinatorics Dataset Repository (ACD Repo), representing either foundational results or open problems in algebraic combinatorics, a subfield of mathematics that studies discrete structures arising from abstract algebra. Further differentiating our dataset collection is the fact that it aims at the conjecturing process. Each dataset includes an open-ended research-level question and a large collection of examples (up to 10M in some cases) from which conjectures should be generated. We describe all nine datasets, the different ways machine learning models can be applied to them (e.g., training with narrow models followed by interpretability analysis or program synthesis with LLMs), and discuss some of the challenges involved in designing datasets like these.

Machines and Mathematical Mutations: Using GNNs to Characterize Quiver Mutation Classes

Machine learning is becoming an increasingly valuable tool in mathematics, enabling one to identify subtle patterns across collections of examples so vast that they would be impossible for a single researcher to feasibly review and analyze. In this work, we use graph neural networks to investigate quiver mutation -- an operation that transforms one quiver (or directed multigraph) into another -- which is central to the theory of cluster algebras with deep connections to geometry, topology, and physics. In the study of cluster algebras, the question of mutation equivalence is of fundamental concern: given two quivers, can one efficiently determine if one quiver can be transformed into the other through a sequence of mutations? Currently, this question has only been resolved in specific cases. In this paper, we use graph neural networks and AI explainability techniques to discover mutation equivalence criteria for the previously unknown case of quivers of type $\tilde{D}_n$. Along the way, we also show that even without explicit training to do so, our model captures structure within its hidden representation that allows us to reconstruct known criteria from type $D_n$, adding to the growing evidence that modern machine learning models are capable of learning abstract and general rules from mathematical data.

Using Higher-Order Moments to Assess the Quality of GAN-generated Image Features

The rapid advancement of Generative Adversarial Networks (GANs) necessitates the need to robustly evaluate these models. Among the established evaluation criteria, the Fr\'{e}chet Inception Distance (FID) has been widely adopted due to its conceptual simplicity, fast computation time, and strong correlation with human perception. However, FID has inherent limitations, mainly stemming from its assumption that feature embeddings follow a Gaussian distribution, and therefore can be defined by their first two moments. As this does not hold in practice, in this paper we explore the importance of third-moments in image feature data and use this information to define a new measure, which we call the Skew Inception Distance (SID). We prove that SID is a pseudometric on probability distributions, show how it extends FID, and present a practical method for its computation. Our numerical experiments support that SID either tracks with FID or, in some cases, aligns more closely with human perception when evaluating image features of ImageNet data.

ICML 2023 Topological Deep Learning Challenge : Design and Results

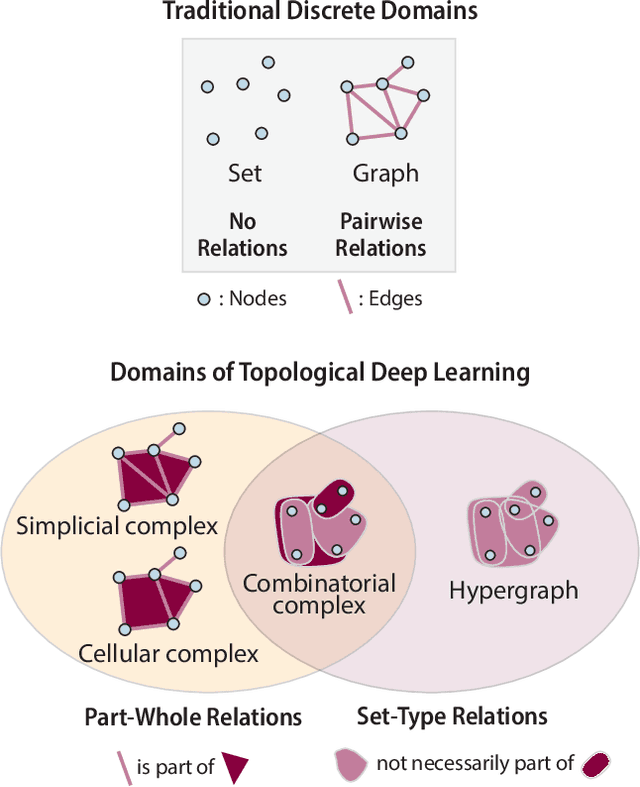
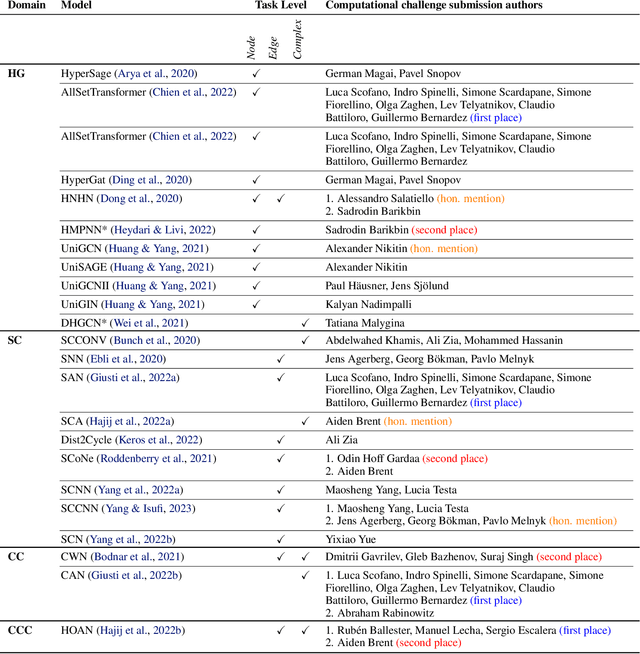
This paper presents the computational challenge on topological deep learning that was hosted within the ICML 2023 Workshop on Topology and Geometry in Machine Learning. The competition asked participants to provide open-source implementations of topological neural networks from the literature by contributing to the python packages TopoNetX (data processing) and TopoModelX (deep learning). The challenge attracted twenty-eight qualifying submissions in its two-month duration. This paper describes the design of the challenge and summarizes its main findings.