Using Higher-Order Moments to Assess the Quality of GAN-generated Image Features

The rapid advancement of Generative Adversarial Networks (GANs) necessitates the need to robustly evaluate these models. Among the established evaluation criteria, the Fr\'{e}chet Inception Distance (FID) has been widely adopted due to its conceptual simplicity, fast computation time, and strong correlation with human perception. However, FID has inherent limitations, mainly stemming from its assumption that feature embeddings follow a Gaussian distribution, and therefore can be defined by their first two moments. As this does not hold in practice, in this paper we explore the importance of third-moments in image feature data and use this information to define a new measure, which we call the Skew Inception Distance (SID). We prove that SID is a pseudometric on probability distributions, show how it extends FID, and present a practical method for its computation. Our numerical experiments support that SID either tracks with FID or, in some cases, aligns more closely with human perception when evaluating image features of ImageNet data.

Seven open problems in applied combinatorics

We present and discuss seven different open problems in applied combinatorics. The application areas relevant to this compilation include quantum computing, algorithmic differentiation, topological data analysis, iterative methods, hypergraph cut algorithms, and power systems.

The SVD of Convolutional Weights: A CNN Interpretability Framework

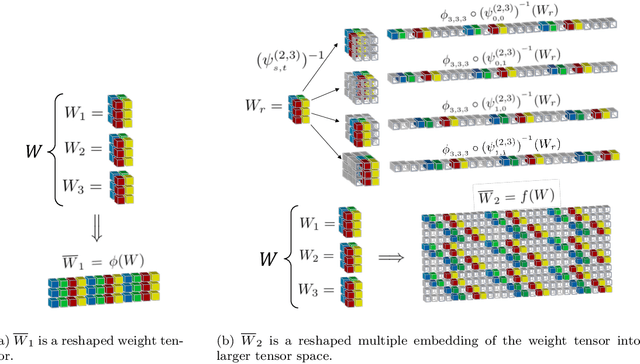
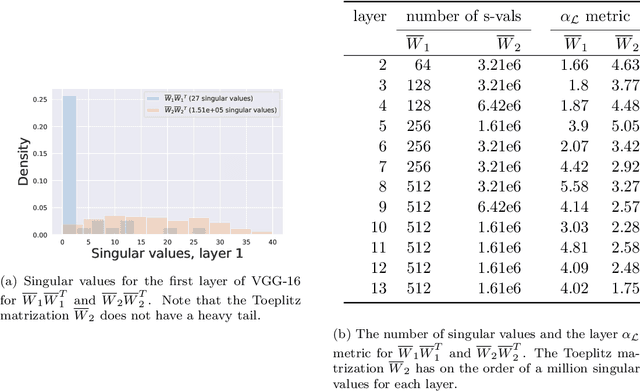
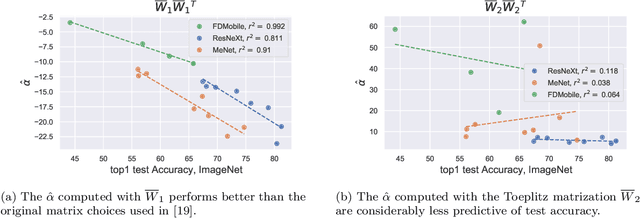
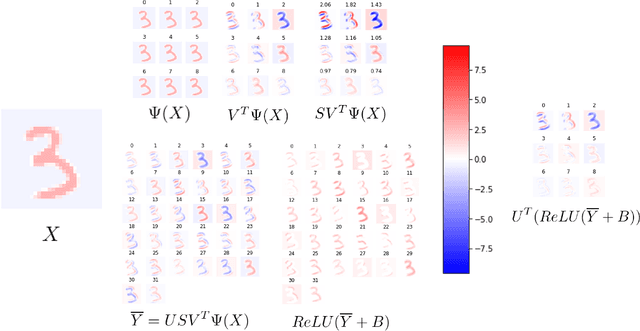
Deep neural networks used for image classification often use convolutional filters to extract distinguishing features before passing them to a linear classifier. Most interpretability literature focuses on providing semantic meaning to convolutional filters to explain a model's reasoning process and confirm its use of relevant information from the input domain. Fully connected layers can be studied by decomposing their weight matrices using a singular value decomposition, in effect studying the correlations between the rows in each matrix to discover the dynamics of the map. In this work we define a singular value decomposition for the weight tensor of a convolutional layer, which provides an analogous understanding of the correlations between filters, exposing the dynamics of the convolutional map. We validate our definition using recent results in random matrix theory. By applying the decomposition across the linear layers of an image classification network we suggest a framework against which interpretability methods might be applied using hypergraphs to model class separation. Rather than looking to the activations to explain the network, we use the singular vectors with the greatest corresponding singular values for each linear layer to identify those features most important to the network. We illustrate our approach with examples and introduce the DeepDataProfiler library, the analysis tool used for this study.

Evaluating generative networks using Gaussian mixtures of image features

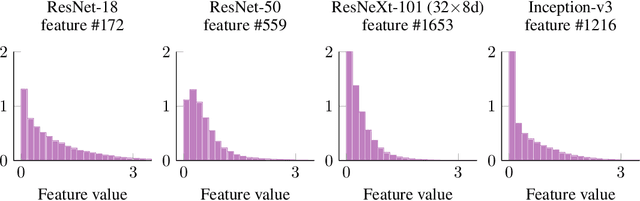
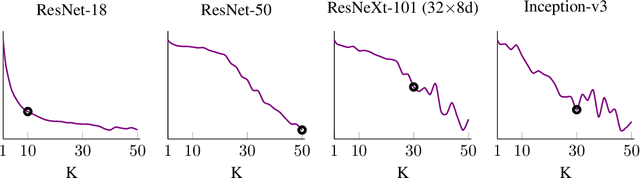
We develop a measure for evaluating the performance of generative networks given two sets of images. A popular performance measure currently used to do this is the Fr\'echet Inception Distance (FID). However, FID assumes that images featurized using the penultimate layer of Inception-v3 follow a Gaussian distribution. This assumption allows FID to be easily computed, since FID uses the 2-Wasserstein distance of two Gaussian distributions fitted to the featurized images. However, we show that Inception-v3 features of the ImageNet dataset are not Gaussian; in particular, each marginal is not Gaussian. To remedy this problem, we model the featurized images using Gaussian mixture models (GMMs) and compute the 2-Wasserstein distance restricted to GMMs. We define a performance measure, which we call WaM, on two sets of images by using Inception-v3 (or another classifier) to featurize the images, estimate two GMMs, and use the restricted 2-Wasserstein distance to compare the GMMs. We experimentally show the advantages of WaM over FID, including how FID is more sensitive than WaM to image perturbations. By modelling the non-Gaussian features obtained from Inception-v3 as GMMs and using a GMM metric, we can more accurately evaluate generative network performance.

Entanglement Induced Barren Plateaus

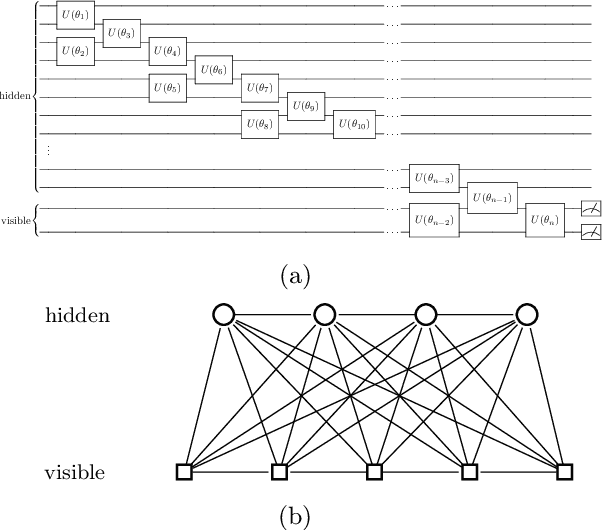
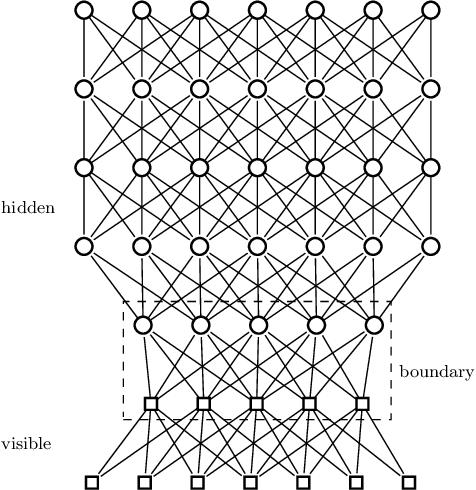
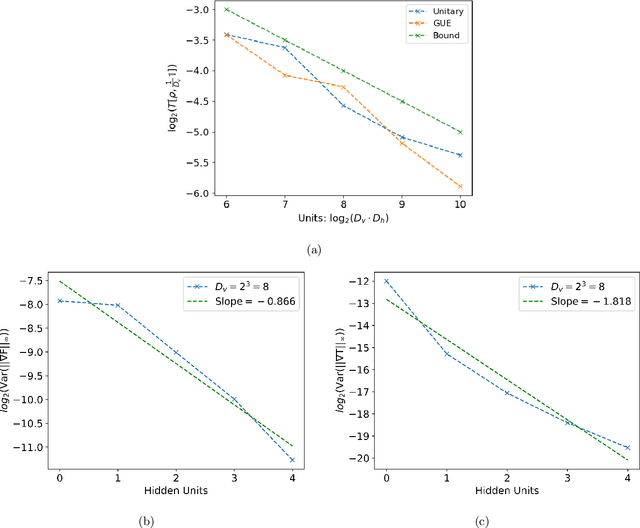
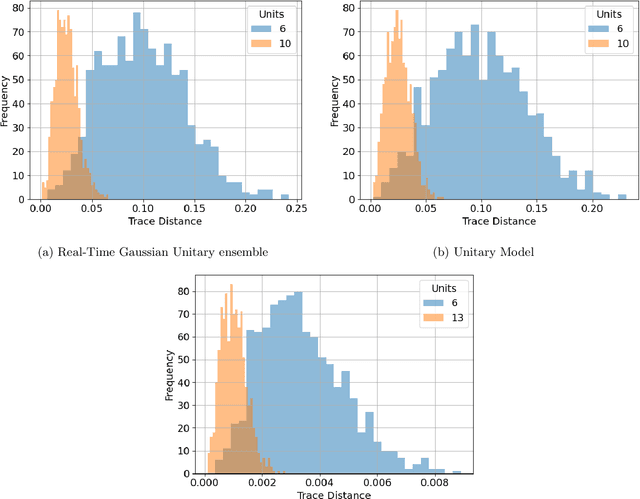
We argue that an excess in entanglement between the visible and hidden units in a Quantum Neural Network can hinder learning. In particular, we show that quantum neural networks that satisfy a volume-law in the entanglement entropy will give rise to models not suitable for learning with high probability. Using arguments from quantum thermodynamics, we then show that this volume law is typical and that there exists a barren plateau in the optimization landscape due to entanglement. More precisely, we show that for any bounded objective function on the visible layers, the Lipshitz constants of the expectation value of that objective function will scale inversely with the dimension of the hidden-subsystem with high probability. We show how this can cause both gradient descent and gradient-free methods to fail. We note that similar problems can happen with quantum Boltzmann machines, although stronger assumptions on the coupling between the hidden/visible subspaces are necessary. We highlight how pretraining such generative models may provide a way to navigate these barren plateaus.

Modeling Atmospheric Data and Identifying Dynamics: Temporal Data-Driven Modeling of Air Pollutants

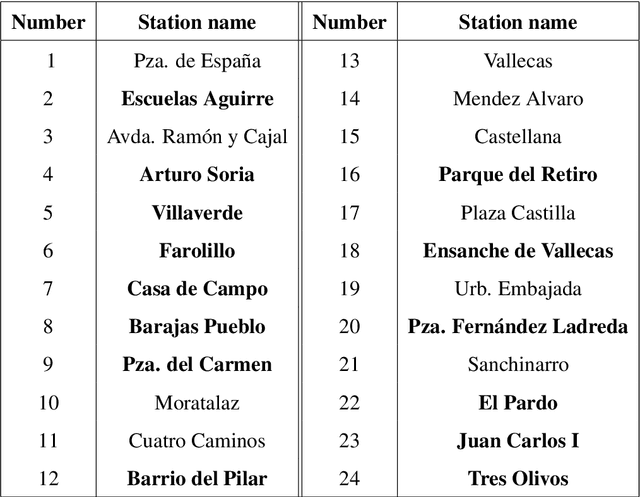
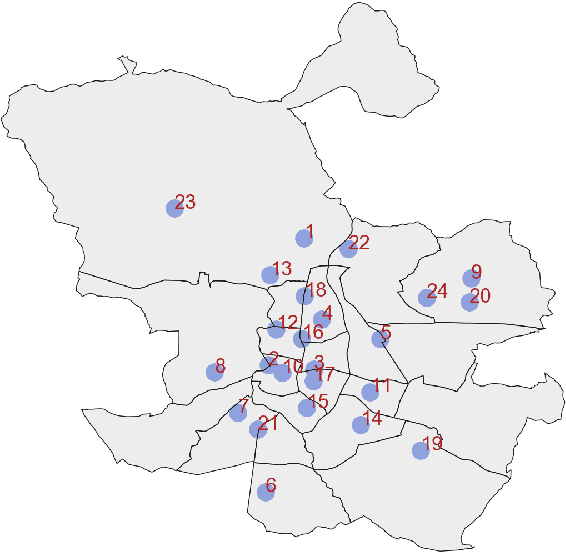
Atmospheric modelling has recently experienced a surge with the advent of deep learning. Most of these models, however, predict concentrations of pollutants following a data-driven approach in which the physical laws that govern their behaviors and relationships remain hidden. With the aid of real-world air quality data collected hourly in different stations throughout Madrid, we present a case study using a series of data-driven techniques with the following goals: (1) Find systems of ordinary differential equations that model the concentration of pollutants and their changes over time; (2) assess the performance and limitations of our models using stability analysis; (3) reconstruct the time series of chemical pollutants not measured in certain stations using delay coordinate embedding results.

Robustness Metrics for Real-World Adversarial Examples

We explore metrics to evaluate the robustness of real-world adversarial attacks, in particular adversarial patches, to changes in environmental conditions. We demonstrate how these metrics can be used to establish model baseline performance and uncover model biases to then compare against real-world adversarial attacks. We establish a custom score for an adversarial condition that is adjusted for different environmental conditions and explore how the score changes with respect to specific environmental factors. Lastly, we propose two use cases for confidence distributions in each environmental condition.