$G$-Mapper: Learning a Cover in the Mapper Construction

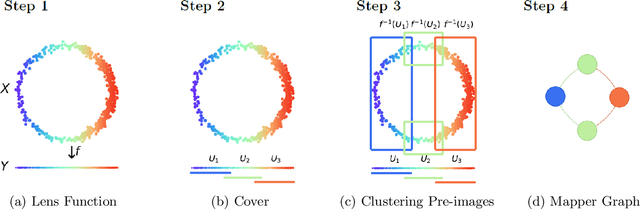
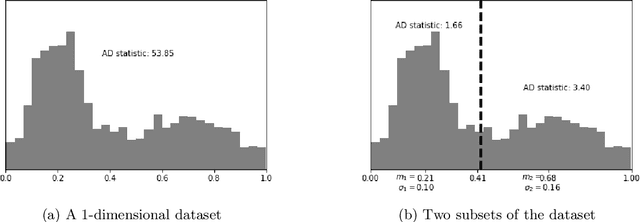
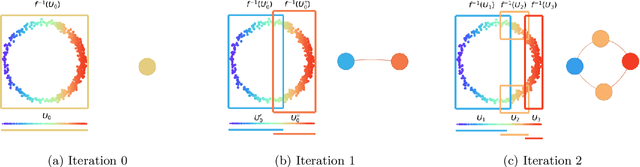
The Mapper algorithm is a visualization technique in topological data analysis (TDA) that outputs a graph reflecting the structure of a given dataset. The Mapper algorithm requires tuning several parameters in order to generate a "nice" Mapper graph. The paper focuses on selecting the cover parameter. We present an algorithm that optimizes the cover of a Mapper graph by splitting a cover repeatedly according to a statistical test for normality. Our algorithm is based on $G$-means clustering which searches for the optimal number of clusters in $k$-means by conducting iteratively the Anderson-Darling test. Our splitting procedure employs a Gaussian mixture model in order to choose carefully the cover based on the distribution of a given data. Experiments for synthetic and real-world datasets demonstrate that our algorithm generates covers so that the Mapper graphs retain the essence of the datasets.

Experimental Observations of the Topology of Convolutional Neural Network Activations

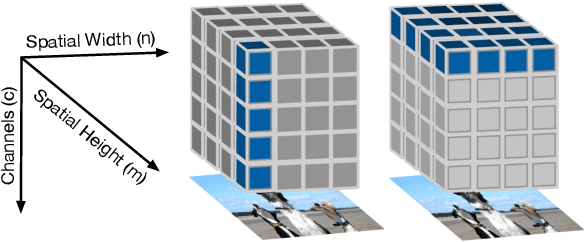
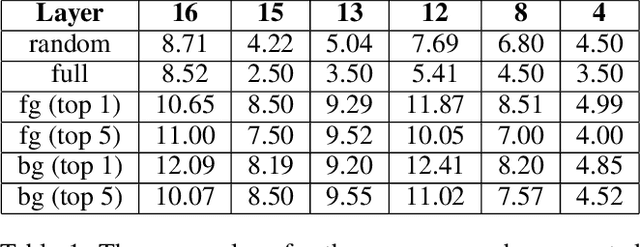
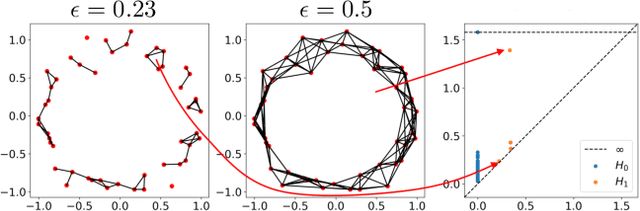
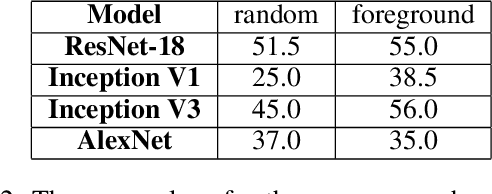
Topological data analysis (TDA) is a branch of computational mathematics, bridging algebraic topology and data science, that provides compact, noise-robust representations of complex structures. Deep neural networks (DNNs) learn millions of parameters associated with a series of transformations defined by the model architecture, resulting in high-dimensional, difficult-to-interpret internal representations of input data. As DNNs become more ubiquitous across multiple sectors of our society, there is increasing recognition that mathematical methods are needed to aid analysts, researchers, and practitioners in understanding and interpreting how these models' internal representations relate to the final classification. In this paper, we apply cutting edge techniques from TDA with the goal of gaining insight into the interpretability of convolutional neural networks used for image classification. We use two common TDA approaches to explore several methods for modeling hidden-layer activations as high-dimensional point clouds, and provide experimental evidence that these point clouds capture valuable structural information about the model's process. First, we demonstrate that a distance metric based on persistent homology can be used to quantify meaningful differences between layers, and we discuss these distances in the broader context of existing representational similarity metrics for neural network interpretability. Second, we show that a mapper graph can provide semantic insight into how these models organize hierarchical class knowledge at each layer. These observations demonstrate that TDA is a useful tool to help deep learning practitioners unlock the hidden structures of their models.

The SVD of Convolutional Weights: A CNN Interpretability Framework

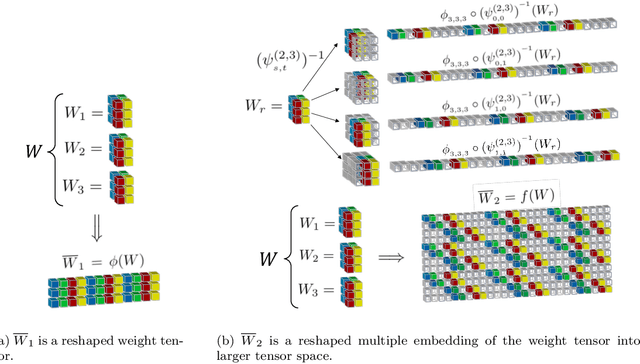
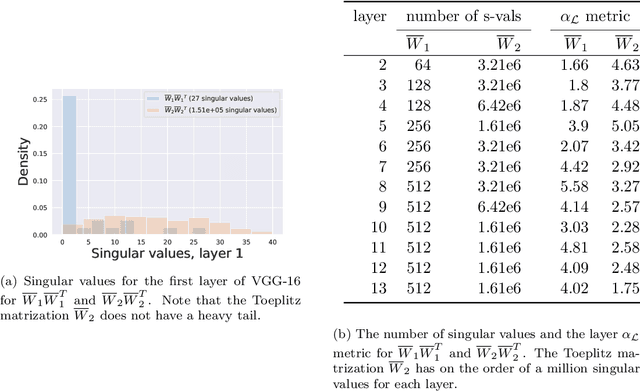
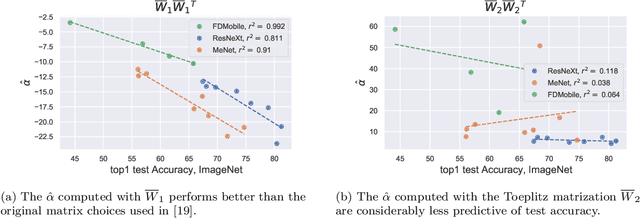
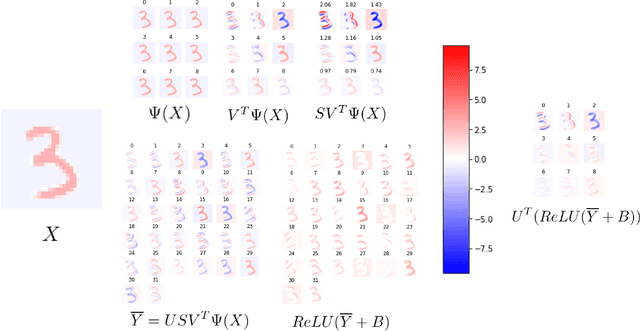
Deep neural networks used for image classification often use convolutional filters to extract distinguishing features before passing them to a linear classifier. Most interpretability literature focuses on providing semantic meaning to convolutional filters to explain a model's reasoning process and confirm its use of relevant information from the input domain. Fully connected layers can be studied by decomposing their weight matrices using a singular value decomposition, in effect studying the correlations between the rows in each matrix to discover the dynamics of the map. In this work we define a singular value decomposition for the weight tensor of a convolutional layer, which provides an analogous understanding of the correlations between filters, exposing the dynamics of the convolutional map. We validate our definition using recent results in random matrix theory. By applying the decomposition across the linear layers of an image classification network we suggest a framework against which interpretability methods might be applied using hypergraphs to model class separation. Rather than looking to the activations to explain the network, we use the singular vectors with the greatest corresponding singular values for each linear layer to identify those features most important to the network. We illustrate our approach with examples and introduce the DeepDataProfiler library, the analysis tool used for this study.

Proceedings of TDA: Applications of Topological Data Analysis to Data Science, Artificial Intelligence, and Machine Learning Workshop at SDM 2022

Topological Data Analysis (TDA) is a rigorous framework that borrows techniques from geometric and algebraic topology, category theory, and combinatorics in order to study the "shape" of such complex high-dimensional data. Research in this area has grown significantly over the last several years bringing a deeply rooted theory to bear on practical applications in areas such as genomics, natural language processing, medicine, cybersecurity, energy, and climate change. Within some of these areas, TDA has also been used to augment AI and ML techniques. We believe there is further utility to be gained in this space that can be facilitated by a workshop bringing together experts (both theorists and practitioners) and non-experts. Currently there is an active community of pure mathematicians with research interests in developing and exploring the theoretical and computational aspects of TDA. Applied mathematicians and other practitioners are also present in community but do not represent a majority. This speaks to the primary aim of this workshop which is to grow a wider community of interest in TDA. By fostering meaningful exchanges between these groups, from across the government, academia, and industry, we hope to create new synergies that can only come through building a mutual comprehensive awareness of the problem and solution spaces.

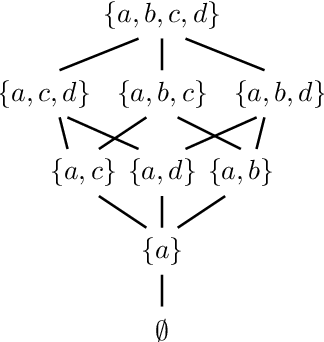
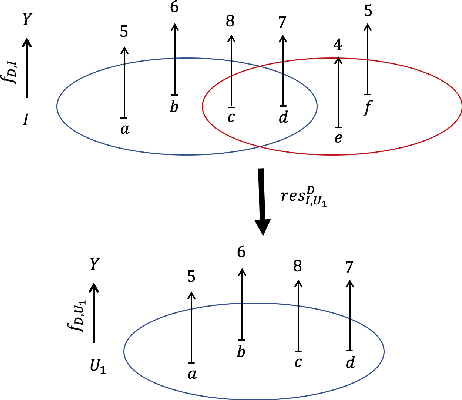
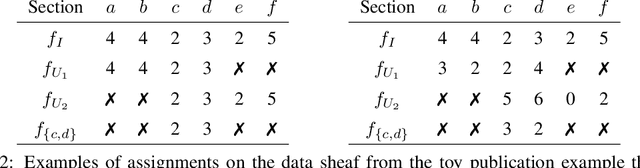
Sheaves as a Framework for Understanding and Interpreting Model Fit

As data grows in size and complexity, finding frameworks which aid in interpretation and analysis has become critical. This is particularly true when data comes from complex systems where extensive structure is available, but must be drawn from peripheral sources. In this paper we argue that in such situations, sheaves can provide a natural framework to analyze how well a statistical model fits at the local level (that is, on subsets of related datapoints) vs the global level (on all the data). The sheaf-based approach that we propose is suitably general enough to be useful in a range of applications, from analyzing sensor networks to understanding the feature space of a deep learning model.

Argumentative Topology: Finding Loop(holes) in Logic

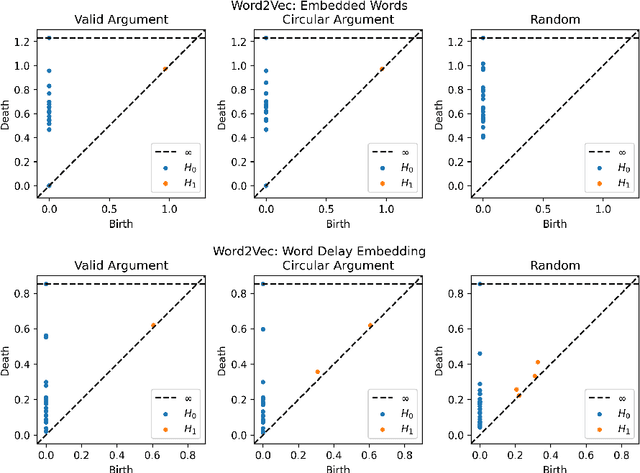
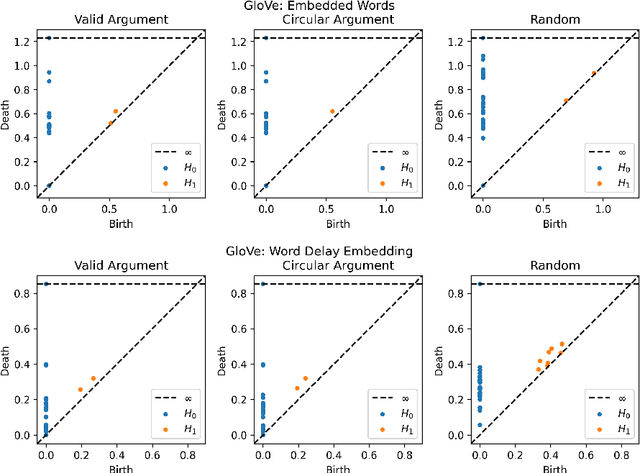
Advances in natural language processing have resulted in increased capabilities with respect to multiple tasks. One of the possible causes of the observed performance gains is the introduction of increasingly sophisticated text representations. While many of the new word embedding techniques can be shown to capture particular notions of sentiment or associative structures, we explore the ability of two different word embeddings to uncover or capture the notion of logical shape in text. To this end we present a novel framework that we call Topological Word Embeddings which leverages mathematical techniques in dynamical system analysis and data driven shape extraction (i.e. topological data analysis). In this preliminary work we show that using a topological delay embedding we are able to capture and extract a different, shape-based notion of logic aimed at answering the question "Can we find a circle in a circular argument?"

Relative Hausdorff Distance for Network Analysis

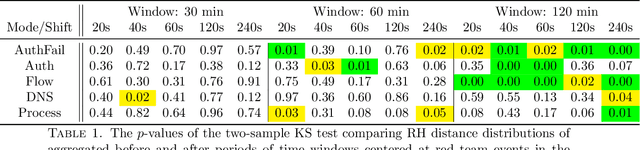
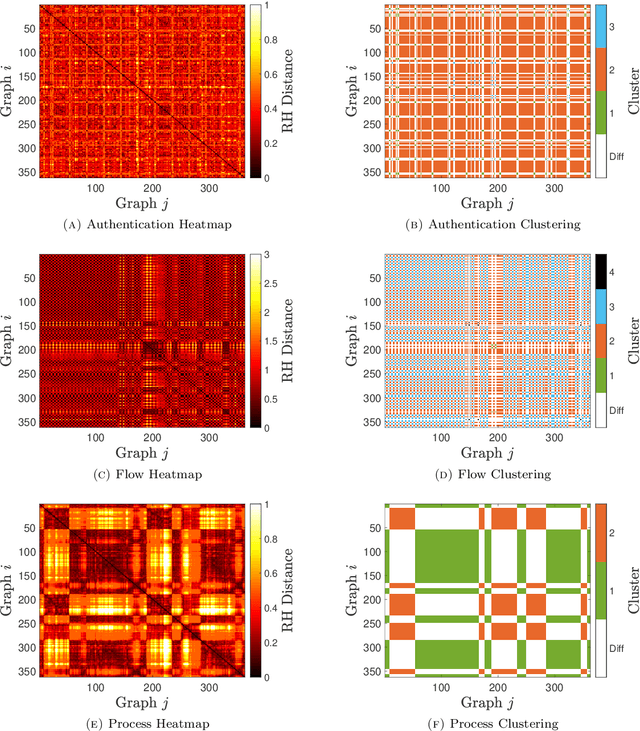
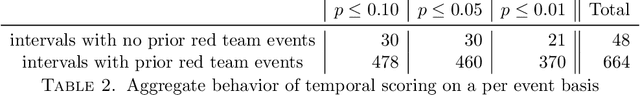
Similarity measures are used extensively in machine learning and data science algorithms. The newly proposed graph Relative Hausdorff (RH) distance is a lightweight yet nuanced similarity measure for quantifying the closeness of two graphs. In this work we study the effectiveness of RH distance as a tool for detecting anomalies in time-evolving graph sequences. We apply RH to cyber data with given red team events, as well to synthetically generated sequences of graphs with planted attacks. In our experiments, the performance of RH distance is at times comparable, and sometimes superior, to graph edit distance in detecting anomalous phenomena. Our results suggest that in appropriate contexts, RH distance has advantages over more computationally intensive similarity measures.