HyperMagNet: A Magnetic Laplacian based Hypergraph Neural Network

In data science, hypergraphs are natural models for data exhibiting multi-way relations, whereas graphs only capture pairwise. Nonetheless, many proposed hypergraph neural networks effectively reduce hypergraphs to undirected graphs via symmetrized matrix representations, potentially losing important information. We propose an alternative approach to hypergraph neural networks in which the hypergraph is represented as a non-reversible Markov chain. We use this Markov chain to construct a complex Hermitian Laplacian matrix - the magnetic Laplacian - which serves as the input to our proposed hypergraph neural network. We study HyperMagNet for the task of node classification, and demonstrate its effectiveness over graph-reduction based hypergraph neural networks.

Scalable tensor methods for nonuniform hypergraphs

While multilinear algebra appears natural for studying the multiway interactions modeled by hypergraphs, tensor methods for general hypergraphs have been stymied by theoretical and practical barriers. A recently proposed adjacency tensor is applicable to nonuniform hypergraphs, but is prohibitively costly to form and analyze in practice. We develop tensor times same vector (TTSV) algorithms for this tensor which improve complexity from $O(n^r)$ to a low-degree polynomial in $r$, where $n$ is the number of vertices and $r$ is the maximum hyperedge size. Our algorithms are implicit, avoiding formation of the order $r$ adjacency tensor. We demonstrate the flexibility and utility of our approach in practice by developing tensor-based hypergraph centrality and clustering algorithms. We also show these tensor measures offer complementary information to analogous graph-reduction approaches on data, and are also able to detect higher-order structure that many existing matrix-based approaches provably cannot.

Seven open problems in applied combinatorics

We present and discuss seven different open problems in applied combinatorics. The application areas relevant to this compilation include quantum computing, algorithmic differentiation, topological data analysis, iterative methods, hypergraph cut algorithms, and power systems.

Relative Hausdorff Distance for Network Analysis

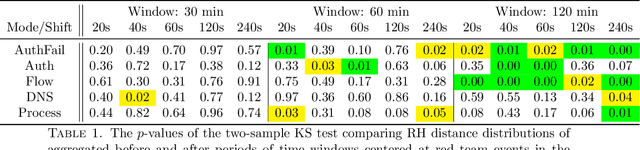
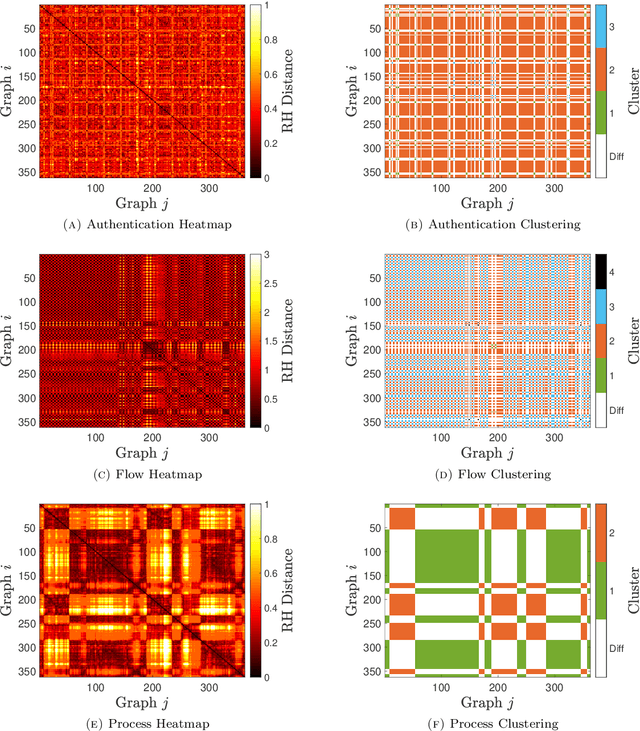
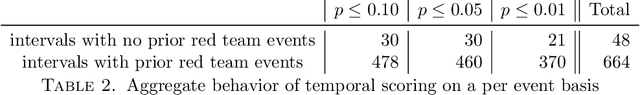
Similarity measures are used extensively in machine learning and data science algorithms. The newly proposed graph Relative Hausdorff (RH) distance is a lightweight yet nuanced similarity measure for quantifying the closeness of two graphs. In this work we study the effectiveness of RH distance as a tool for detecting anomalies in time-evolving graph sequences. We apply RH to cyber data with given red team events, as well to synthetically generated sequences of graphs with planted attacks. In our experiments, the performance of RH distance is at times comparable, and sometimes superior, to graph edit distance in detecting anomalous phenomena. Our results suggest that in appropriate contexts, RH distance has advantages over more computationally intensive similarity measures.