Seven open problems in applied combinatorics

We present and discuss seven different open problems in applied combinatorics. The application areas relevant to this compilation include quantum computing, algorithmic differentiation, topological data analysis, iterative methods, hypergraph cut algorithms, and power systems.

A Topological Data Analysis Based Classifier

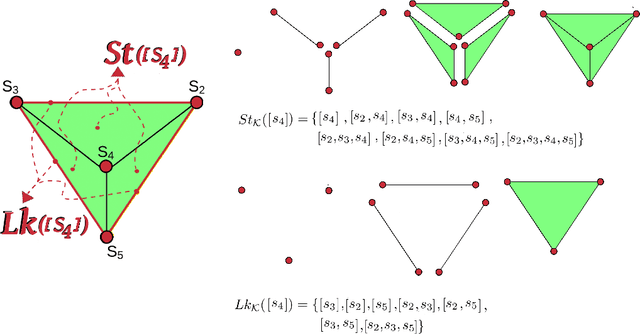
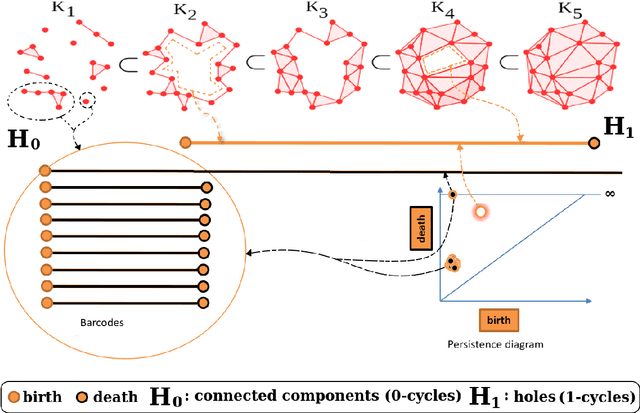
Topological Data Analysis (TDA) is an emergent field that aims to discover topological information hidden in a dataset. TDA tools have been commonly used to create filters and topological descriptors to improve Machine Learning (ML) methods. This paper proposes an algorithm that applies TDA directly to multi-class classification problems, without any further ML stage, showing advantages for imbalanced datasets. The proposed algorithm builds a filtered simplicial complex on the dataset. Persistent Homology (PH) is applied to guide the selection of a sub-complex where unlabeled points obtain the label with the majority of votes from labeled neighboring points. We select 8 datasets with different dimensions, degrees of class overlap and imbalanced samples per class. On average, the proposed TDABC method was better than KNN and weighted-KNN. It behaves competitively with Local SVM and Random Forest baseline classifiers in balanced datasets, and it outperforms all baseline methods classifying entangled and minority classes.

Classification based on Topological Data Analysis

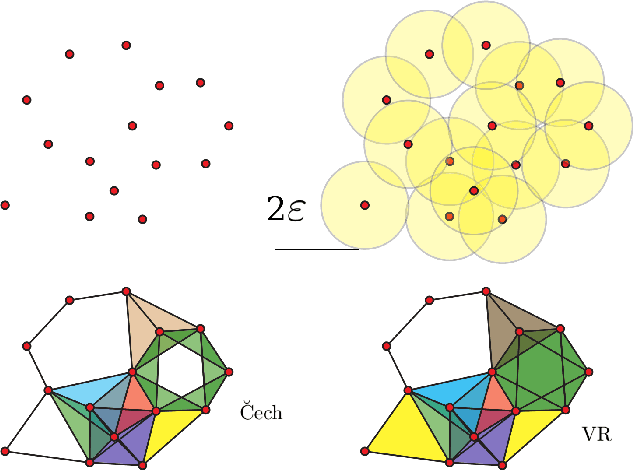
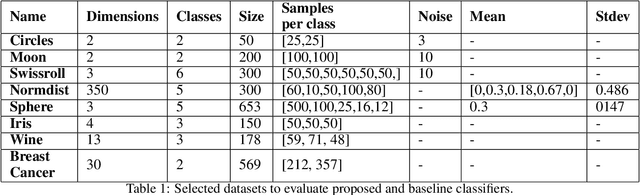
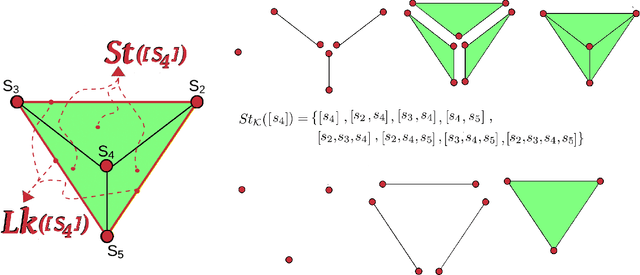
Topological Data Analysis (TDA) is an emergent field that aims to discover topological information hidden in a dataset. TDA tools have been commonly used to create filters and topological descriptors to improve Machine Learning (ML) methods. This paper proposes an algorithm that applies TDA directly to multi-class classification problems, even imbalanced datasets, without any further ML stage. The proposed algorithm built a filtered simplicial complex on the dataset. Persistent homology is then applied to guide choosing a sub-complex where unlabeled points obtain the label with most votes from labeled neighboring points. To assess the proposed method, 8 datasets were selected with several degrees of class entanglement, variability on the samples per class, and dimensionality. On average, the proposed TDABC method was capable of overcoming baseline classifiers (wk-NN and k-NN) in each of the computed metrics, especially on classifying entangled and minority classes.