Nancy Hitschfeld
A Class of Topological Pseudodistances for Fast Comparison of Persistence Diagrams
Feb 22, 2024Abstract:Persistence diagrams (PD)s play a central role in topological data analysis, and are used in an ever increasing variety of applications. The comparison of PD data requires computing comparison metrics among large sets of PDs, with metrics which are accurate, theoretically sound, and fast to compute. Especially for denser multi-dimensional PDs, such comparison metrics are lacking. While on the one hand, Wasserstein-type distances have high accuracy and theoretical guarantees, they incur high computational cost. On the other hand, distances between vectorizations such as Persistence Statistics (PS)s have lower computational cost, but lack the accuracy guarantees and in general they are not guaranteed to distinguish PDs (i.e. the two PS vectors of different PDs may be equal). In this work we introduce a class of pseudodistances called Extended Topological Pseudodistances (ETD)s, which have tunable complexity, and can approximate Sliced and classical Wasserstein distances at the high-complexity extreme, while being computationally lighter and close to Persistence Statistics at the lower complexity extreme, and thus allow users to interpolate between the two metrics. We build theoretical comparisons to show how to fit our new distances at an intermediate level between persistence vectorizations and Wasserstein distances. We also experimentally verify that ETDs outperform PSs in terms of accuracy and outperform Wasserstein and Sliced Wasserstein distances in terms of computational complexity.
A Topological Data Analysis Based Classifier
Nov 10, 2021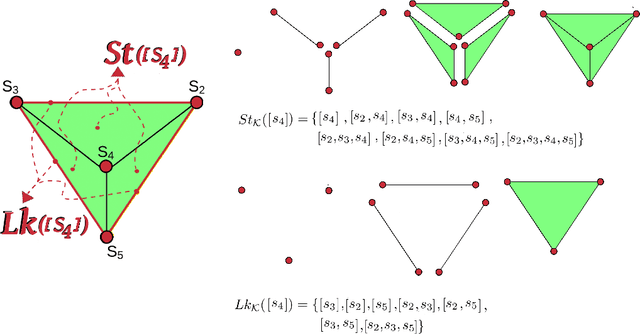
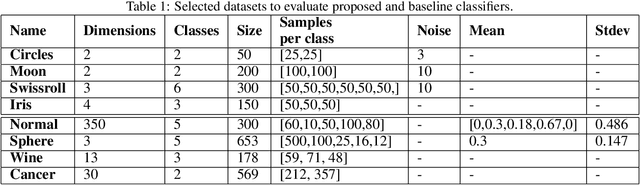
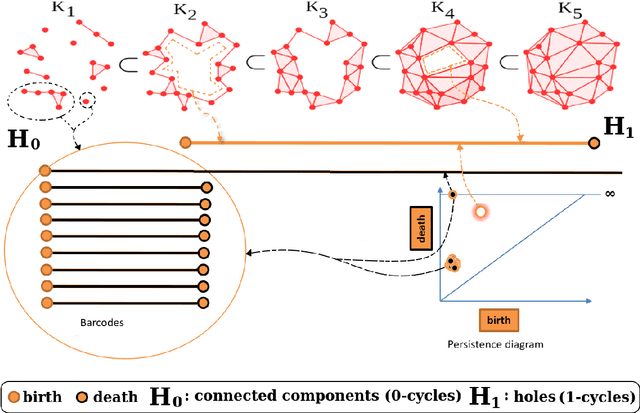

Abstract:Topological Data Analysis (TDA) is an emergent field that aims to discover topological information hidden in a dataset. TDA tools have been commonly used to create filters and topological descriptors to improve Machine Learning (ML) methods. This paper proposes an algorithm that applies TDA directly to multi-class classification problems, without any further ML stage, showing advantages for imbalanced datasets. The proposed algorithm builds a filtered simplicial complex on the dataset. Persistent Homology (PH) is applied to guide the selection of a sub-complex where unlabeled points obtain the label with the majority of votes from labeled neighboring points. We select 8 datasets with different dimensions, degrees of class overlap and imbalanced samples per class. On average, the proposed TDABC method was better than KNN and weighted-KNN. It behaves competitively with Local SVM and Random Forest baseline classifiers in balanced datasets, and it outperforms all baseline methods classifying entangled and minority classes.
Classification based on Topological Data Analysis
Feb 07, 2021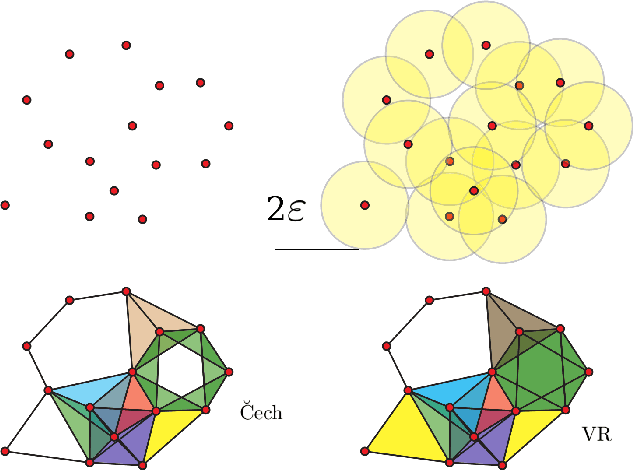
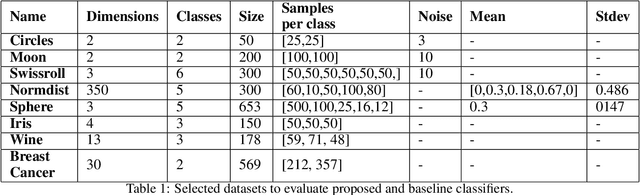
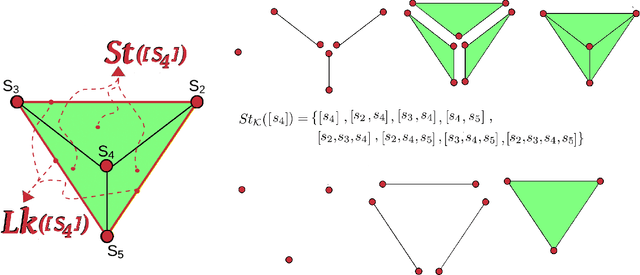

Abstract:Topological Data Analysis (TDA) is an emergent field that aims to discover topological information hidden in a dataset. TDA tools have been commonly used to create filters and topological descriptors to improve Machine Learning (ML) methods. This paper proposes an algorithm that applies TDA directly to multi-class classification problems, even imbalanced datasets, without any further ML stage. The proposed algorithm built a filtered simplicial complex on the dataset. Persistent homology is then applied to guide choosing a sub-complex where unlabeled points obtain the label with most votes from labeled neighboring points. To assess the proposed method, 8 datasets were selected with several degrees of class entanglement, variability on the samples per class, and dimensionality. On average, the proposed TDABC method was capable of overcoming baseline classifiers (wk-NN and k-NN) in each of the computed metrics, especially on classifying entangled and minority classes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge