Recurrent Equivariant Constraint Modulation: Learning Per-Layer Symmetry Relaxation from Data

Equivariant neural networks exploit underlying task symmetries to improve generalization, but strict equivariance constraints can induce more complex optimization dynamics that can hinder learning. Prior work addresses these limitations by relaxing strict equivariance during training, but typically relies on prespecified, explicit, or implicit target levels of relaxation for each network layer, which are task-dependent and costly to tune. We propose Recurrent Equivariant Constraint Modulation (RECM), a layer-wise constraint modulation mechanism that learns appropriate relaxation levels solely from the training signal and the symmetry properties of each layer's input-target distribution, without requiring any prior knowledge about the task-dependent target relaxation level. We demonstrate that under the proposed RECM update, the relaxation level of each layer provably converges to a value upper-bounded by its symmetry gap, namely the degree to which its input-target distribution deviates from exact symmetry. Consequently, layers processing symmetric distributions recover full equivariance, while those with approximate symmetries retain sufficient flexibility to learn non-symmetric solutions when warranted by the data. Empirically, RECM outperforms prior methods across diverse exact and approximate equivariant tasks, including the challenging molecular conformer generation on the GEOM-Drugs dataset.

A Comunication Framework for Compositional Generation

Compositionality and compositional generalization--the ability to understand novel combinations of known concepts--are central characteristics of human language and are hypothesized to be essential for human cognition. In machine learning, the emergence of this property has been studied in a communication game setting, where independent agents (a sender and a receiver) converge to a shared encoding policy from a set of states to a space of discrete messages, where the receiver can correctly reconstruct the states observed by the sender using only the sender's messages. The use of communication games in generation tasks is still largely unexplored, with recent methods for compositional generation focusing mainly on the use of supervised guidance (either through class labels or text). In this work, we take the first steps to fill this gap, and we present a self-supervised generative communication game-based framework for creating compositional encodings in learned representations from pre-trained encoder-decoder models. In an Iterated Learning (IL) protocol involving a sender and a receiver, we apply alternating pressures for compression and diversity of encoded discrete messages, so that the protocol converges to an efficient but unambiguous encoding. Approximate message entropy regularization is used to favor compositional encodings. Our framework is based on rigorous justifications and proofs of defining and balancing the concepts of Eficiency, Unambiguity and Non-Holisticity in encoding. We test our method on the compositional image dataset Shapes3D, demonstrating robust performance in both reconstruction and compositionality metrics, surpassing other tested discrete message frameworks.

Symmetry-Based Structured Matrices for Efficient Approximately Equivariant Networks

There has been much recent interest in designing symmetry-aware neural networks (NNs) exhibiting relaxed equivariance. Such NNs aim to interpolate between being exactly equivariant and being fully flexible, affording consistent performance benefits. In a separate line of work, certain structured parameter matrices -- those with displacement structure, characterized by low displacement rank (LDR) -- have been used to design small-footprint NNs. Displacement structure enables fast function and gradient evaluation, but permits accurate approximations via compression primarily to classical convolutional neural networks (CNNs). In this work, we propose a general framework -- based on a novel construction of symmetry-based structured matrices -- to build approximately equivariant NNs with significantly reduced parameter counts. Our framework integrates the two aforementioned lines of work via the use of so-called Group Matrices (GMs), a forgotten precursor to the modern notion of regular representations of finite groups. GMs allow the design of structured matrices -- resembling LDR matrices -- which generalize the linear operations of a classical CNN from cyclic groups to general finite groups and their homogeneous spaces. We show that GMs can be employed to extend all the elementary operations of CNNs to general discrete groups. Further, the theory of structured matrices based on GMs provides a generalization of LDR theory focussed on matrices with cyclic structure, providing a tool for implementing approximate equivariance for discrete groups. We test GM-based architectures on a variety of tasks in the presence of relaxed symmetry. We report that our framework consistently performs competitively compared to approximately equivariant NNs, and other structured matrix-based compression frameworks, sometimes with a one or two orders of magnitude lower parameter count.

Fisher Flow Matching for Generative Modeling over Discrete Data

Generative modeling over discrete data has recently seen numerous success stories, with applications spanning language modeling, biological sequence design, and graph-structured molecular data. The predominant generative modeling paradigm for discrete data is still autoregressive, with more recent alternatives based on diffusion or flow-matching falling short of their impressive performance in continuous data settings, such as image or video generation. In this work, we introduce Fisher-Flow, a novel flow-matching model for discrete data. Fisher-Flow takes a manifestly geometric perspective by considering categorical distributions over discrete data as points residing on a statistical manifold equipped with its natural Riemannian metric: the $\textit{Fisher-Rao metric}$. As a result, we demonstrate discrete data itself can be continuously reparameterised to points on the positive orthant of the $d$-hypersphere $\mathbb{S}^d_+$, which allows us to define flows that map any source distribution to target in a principled manner by transporting mass along (closed-form) geodesics of $\mathbb{S}^d_+$. Furthermore, the learned flows in Fisher-Flow can be further bootstrapped by leveraging Riemannian optimal transport leading to improved training dynamics. We prove that the gradient flow induced by Fisher-Flow is optimal in reducing the forward KL divergence. We evaluate Fisher-Flow on an array of synthetic and diverse real-world benchmarks, including designing DNA Promoter, and DNA Enhancer sequences. Empirically, we find that Fisher-Flow improves over prior diffusion and flow-matching models on these benchmarks.

Understanding the dynamics of the frequency bias in neural networks

Recent works have shown that traditional Neural Network (NN) architectures display a marked frequency bias in the learning process. Namely, the NN first learns the low-frequency features before learning the high-frequency ones. In this study, we rigorously develop a partial differential equation (PDE) that unravels the frequency dynamics of the error for a 2-layer NN in the Neural Tangent Kernel regime. Furthermore, using this insight, we explicitly demonstrate how an appropriate choice of distributions for the initialization weights can eliminate or control the frequency bias. We focus our study on the Fourier Features model, an NN where the first layer has sine and cosine activation functions, with frequencies sampled from a prescribed distribution. In this setup, we experimentally validate our theoretical results and compare the NN dynamics to the solution of the PDE using the finite element method. Finally, we empirically show that the same principle extends to multi-layer NNs.

Long Tail Image Generation Through Feature Space Augmentation and Iterated Learning

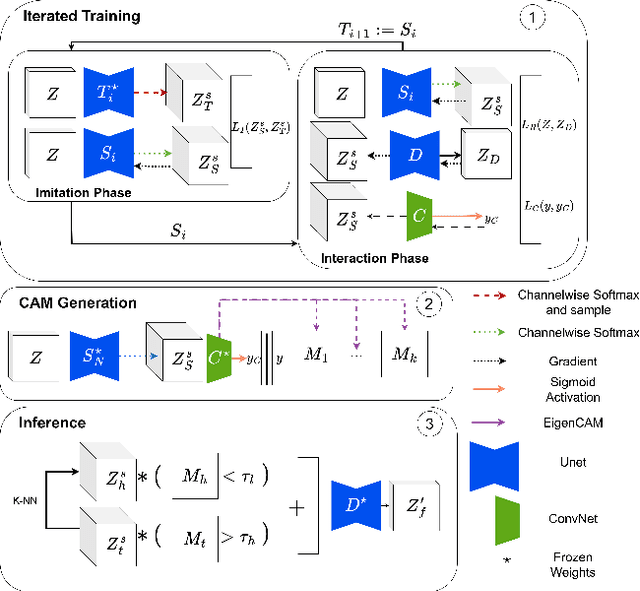
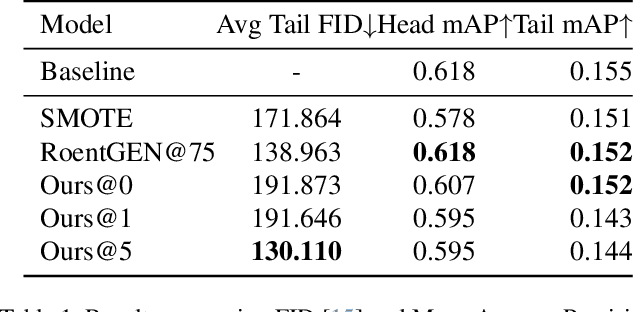
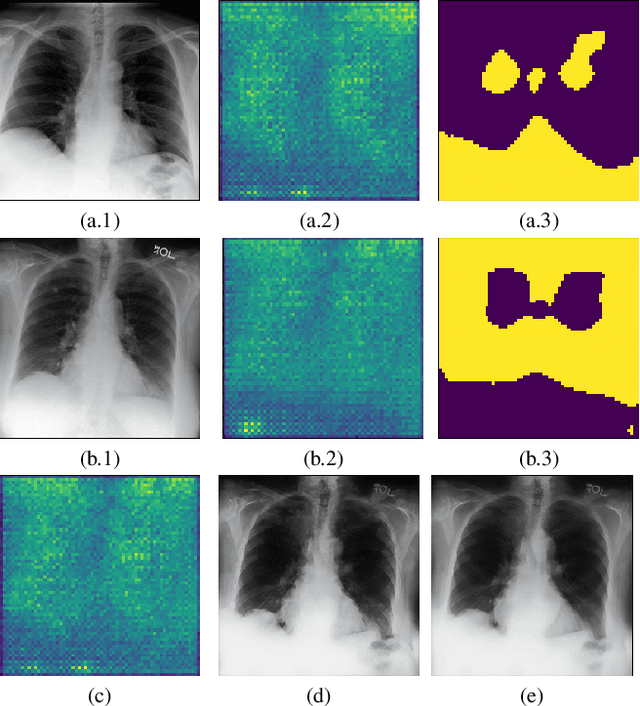
Image and multimodal machine learning tasks are very challenging to solve in the case of poorly distributed data. In particular, data availability and privacy restrictions exacerbate these hurdles in the medical domain. The state of the art in image generation quality is held by Latent Diffusion models, making them prime candidates for tackling this problem. However, a few key issues still need to be solved, such as the difficulty in generating data from under-represented classes and a slow inference process. To mitigate these issues, we propose a new method for image augmentation in long-tailed data based on leveraging the rich latent space of pre-trained Stable Diffusion Models. We create a modified separable latent space to mix head and tail class examples. We build this space via Iterated Learning of underlying sparsified embeddings, which we apply to task-specific saliency maps via a K-NN approach. Code is available at https://github.com/SugarFreeManatee/Feature-Space-Augmentation-and-Iterated-Learning

A Class of Topological Pseudodistances for Fast Comparison of Persistence Diagrams

Persistence diagrams (PD)s play a central role in topological data analysis, and are used in an ever increasing variety of applications. The comparison of PD data requires computing comparison metrics among large sets of PDs, with metrics which are accurate, theoretically sound, and fast to compute. Especially for denser multi-dimensional PDs, such comparison metrics are lacking. While on the one hand, Wasserstein-type distances have high accuracy and theoretical guarantees, they incur high computational cost. On the other hand, distances between vectorizations such as Persistence Statistics (PS)s have lower computational cost, but lack the accuracy guarantees and in general they are not guaranteed to distinguish PDs (i.e. the two PS vectors of different PDs may be equal). In this work we introduce a class of pseudodistances called Extended Topological Pseudodistances (ETD)s, which have tunable complexity, and can approximate Sliced and classical Wasserstein distances at the high-complexity extreme, while being computationally lighter and close to Persistence Statistics at the lower complexity extreme, and thus allow users to interpolate between the two metrics. We build theoretical comparisons to show how to fit our new distances at an intermediate level between persistence vectorizations and Wasserstein distances. We also experimentally verify that ETDs outperform PSs in terms of accuracy and outperform Wasserstein and Sliced Wasserstein distances in terms of computational complexity.

Position Paper: Generalized grammar rules and structure-based generalization beyond classical equivariance for lexical tasks and transduction

Compositional generalization is one of the main properties which differentiates lexical learning in humans from state-of-art neural networks. We propose a general framework for building models that can generalize compositionally using the concept of Generalized Grammar Rules (GGRs), a class of symmetry-based compositional constraints for transduction tasks, which we view as a transduction analogue of equivariance constraints in physics-inspired tasks. Besides formalizing generalized notions of symmetry for language transduction, our framework is general enough to contain many existing works as special cases. We present ideas on how GGRs might be implemented, and in the process draw connections to reinforcement learning and other areas of research.

Approximation-Generalization Trade-offs under (Approximate) Group Equivariance

The explicit incorporation of task-specific inductive biases through symmetry has emerged as a general design precept in the development of high-performance machine learning models. For example, group equivariant neural networks have demonstrated impressive performance across various domains and applications such as protein and drug design. A prevalent intuition about such models is that the integration of relevant symmetry results in enhanced generalization. Moreover, it is posited that when the data and/or the model may only exhibit $\textit{approximate}$ or $\textit{partial}$ symmetry, the optimal or best-performing model is one where the model symmetry aligns with the data symmetry. In this paper, we conduct a formal unified investigation of these intuitions. To begin, we present general quantitative bounds that demonstrate how models capturing task-specific symmetries lead to improved generalization. In fact, our results do not require the transformations to be finite or even form a group and can work with partial or approximate equivariance. Utilizing this quantification, we examine the more general question of model mis-specification i.e. when the model symmetries don't align with the data symmetries. We establish, for a given symmetry group, a quantitative comparison between the approximate/partial equivariance of the model and that of the data distribution, precisely connecting model equivariance error and data equivariance error. Our result delineates conditions under which the model equivariance error is optimal, thereby yielding the best-performing model for the given task and data.

Three iterations of $$-WL test distinguish non isometric clouds of $d$-dimensional points

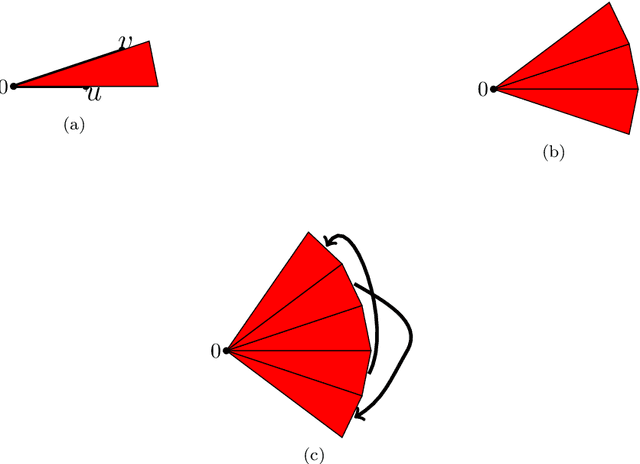
The Weisfeiler--Lehman (WL) test is a fundamental iterative algorithm for checking isomorphism of graphs. It has also been observed that it underlies the design of several graph neural network architectures, whose capabilities and performance can be understood in terms of the expressive power of this test. Motivated by recent developments in machine learning applications to datasets involving three-dimensional objects, we study when the WL test is {\em complete} for clouds of euclidean points represented by complete distance graphs, i.e., when it can distinguish, up to isometry, any arbitrary such cloud. Our main result states that the $(d-1)$-dimensional WL test is complete for point clouds in $d$-dimensional Euclidean space, for any $d\ge 2$, and that only three iterations of the test suffice. Our result is tight for $d = 2, 3$. We also observe that the $d$-dimensional WL test only requires one iteration to achieve completeness.