SIDDA: SInkhorn Dynamic Domain Adaptation for Image Classification with Equivariant Neural Networks

Modern neural networks (NNs) often do not generalize well in the presence of a "covariate shift"; that is, in situations where the training and test data distributions differ, but the conditional distribution of classification labels remains unchanged. In such cases, NN generalization can be reduced to a problem of learning more domain-invariant features. Domain adaptation (DA) methods include a range of techniques aimed at achieving this; however, these methods have struggled with the need for extensive hyperparameter tuning, which then incurs significant computational costs. In this work, we introduce SIDDA, an out-of-the-box DA training algorithm built upon the Sinkhorn divergence, that can achieve effective domain alignment with minimal hyperparameter tuning and computational overhead. We demonstrate the efficacy of our method on multiple simulated and real datasets of varying complexity, including simple shapes, handwritten digits, and real astronomical observations. SIDDA is compatible with a variety of NN architectures, and it works particularly well in improving classification accuracy and model calibration when paired with equivariant neural networks (ENNs). We find that SIDDA enhances the generalization capabilities of NNs, achieving up to a $\approx40\%$ improvement in classification accuracy on unlabeled target data. We also study the efficacy of DA on ENNs with respect to the varying group orders of the dihedral group $D_N$, and find that the model performance improves as the degree of equivariance increases. Finally, we find that SIDDA enhances model calibration on both source and target data--achieving over an order of magnitude improvement in the ECE and Brier score. SIDDA's versatility, combined with its automated approach to domain alignment, has the potential to advance multi-dataset studies by enabling the development of highly generalizable models.

DeepUQ: Assessing the Aleatoric Uncertainties from two Deep Learning Methods

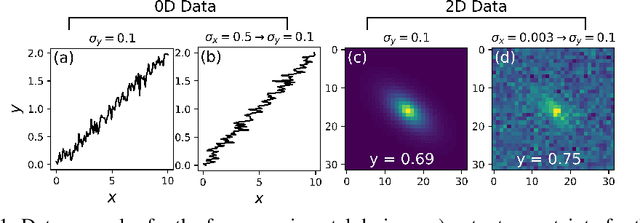
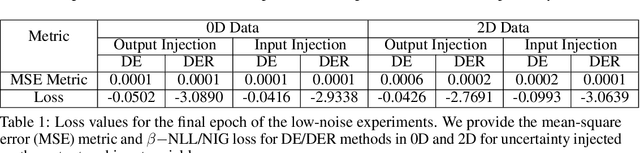
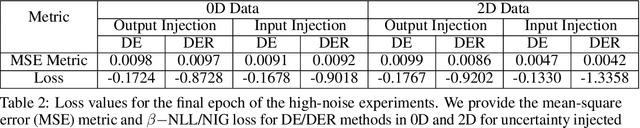
Assessing the quality of aleatoric uncertainty estimates from uncertainty quantification (UQ) deep learning methods is important in scientific contexts, where uncertainty is physically meaningful and important to characterize and interpret exactly. We systematically compare aleatoric uncertainty measured by two UQ techniques, Deep Ensembles (DE) and Deep Evidential Regression (DER). Our method focuses on both zero-dimensional (0D) and two-dimensional (2D) data, to explore how the UQ methods function for different data dimensionalities. We investigate uncertainty injected on the input and output variables and include a method to propagate uncertainty in the case of input uncertainty so that we can compare the predicted aleatoric uncertainty to the known values. We experiment with three levels of noise. The aleatoric uncertainty predicted across all models and experiments scales with the injected noise level. However, the predicted uncertainty is miscalibrated to $\rm{std}(\sigma_{\rm al})$ with the true uncertainty for half of the DE experiments and almost all of the DER experiments. The predicted uncertainty is the least accurate for both UQ methods for the 2D input uncertainty experiment and the high-noise level. While these results do not apply to more complex data, they highlight that further research on post-facto calibration for these methods would be beneficial, particularly for high-noise and high-dimensional settings.

Neural Network Prediction of Strong Lensing Systems with Domain Adaptation and Uncertainty Quantification

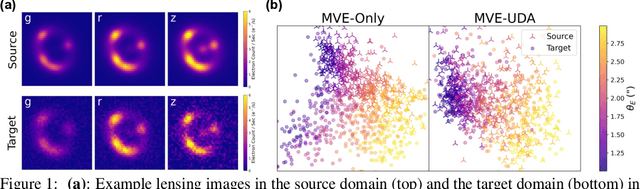
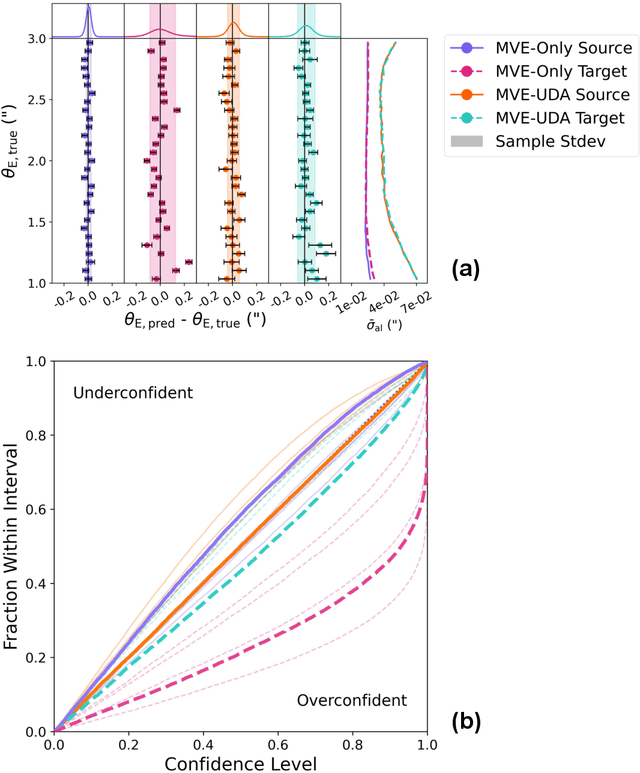
Modeling strong gravitational lenses is computationally expensive for the complex data from modern and next-generation cosmic surveys. Deep learning has emerged as a promising approach for finding lenses and predicting lensing parameters, such as the Einstein radius. Mean-variance Estimators (MVEs) are a common approach for obtaining aleatoric (data) uncertainties from a neural network prediction. However, neural networks have not been demonstrated to perform well on out-of-domain target data successfully - e.g., when trained on simulated data and applied to real, observational data. In this work, we perform the first study of the efficacy of MVEs in combination with unsupervised domain adaptation (UDA) on strong lensing data. The source domain data is noiseless, and the target domain data has noise mimicking modern cosmology surveys. We find that adding UDA to MVE increases the accuracy on the target data by a factor of about two over an MVE model without UDA. Including UDA also permits much more well-calibrated aleatoric uncertainty predictions. Advancements in this approach may enable future applications of MVE models to real observational data.

Domain-Adaptive Neural Posterior Estimation for Strong Gravitational Lens Analysis

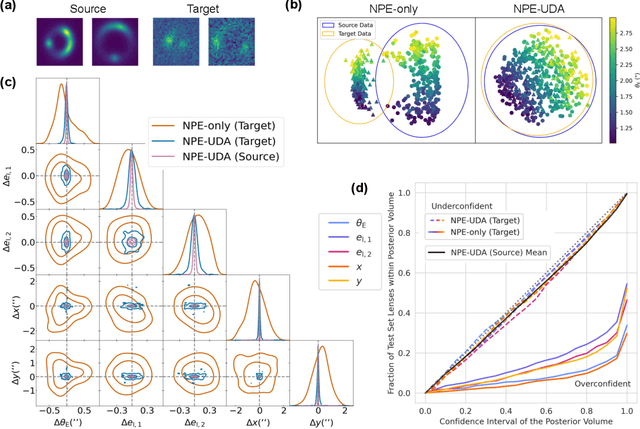
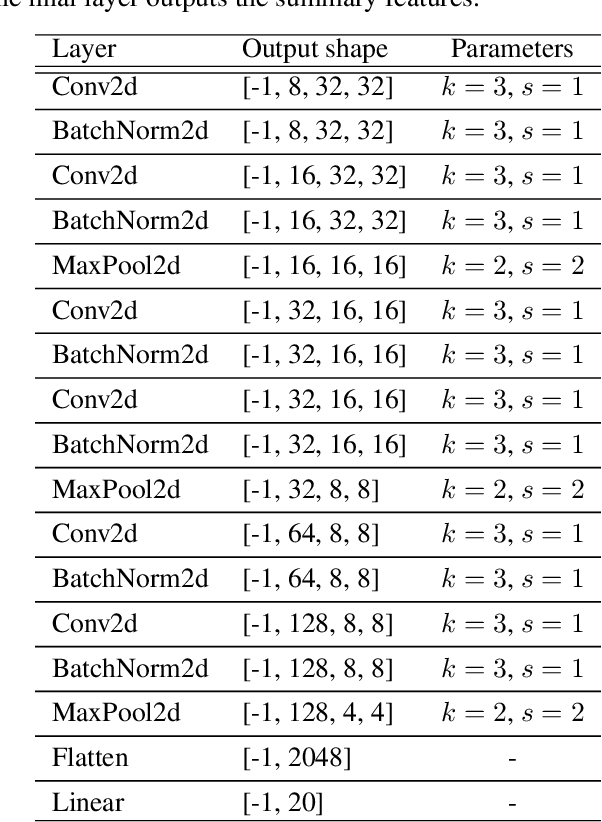
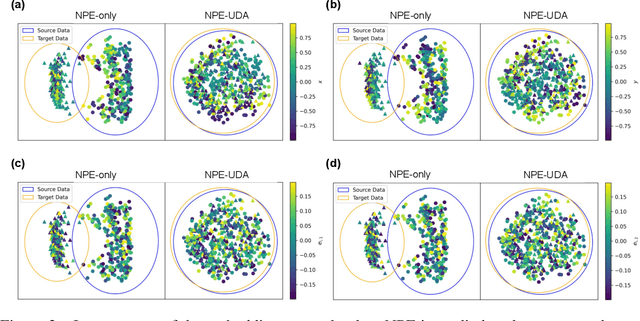
Modeling strong gravitational lenses is prohibitively expensive for modern and next-generation cosmic survey data. Neural posterior estimation (NPE), a simulation-based inference (SBI) approach, has been studied as an avenue for efficient analysis of strong lensing data. However, NPE has not been demonstrated to perform well on out-of-domain target data -- e.g., when trained on simulated data and then applied to real, observational data. In this work, we perform the first study of the efficacy of NPE in combination with unsupervised domain adaptation (UDA). The source domain is noiseless, and the target domain has noise mimicking modern cosmology surveys. We find that combining UDA and NPE improves the accuracy of the inference by 1-2 orders of magnitude and significantly improves the posterior coverage over an NPE model without UDA. We anticipate that this combination of approaches will help enable future applications of NPE models to real observational data.

Symmetry-Based Structured Matrices for Efficient Approximately Equivariant Networks

There has been much recent interest in designing symmetry-aware neural networks (NNs) exhibiting relaxed equivariance. Such NNs aim to interpolate between being exactly equivariant and being fully flexible, affording consistent performance benefits. In a separate line of work, certain structured parameter matrices -- those with displacement structure, characterized by low displacement rank (LDR) -- have been used to design small-footprint NNs. Displacement structure enables fast function and gradient evaluation, but permits accurate approximations via compression primarily to classical convolutional neural networks (CNNs). In this work, we propose a general framework -- based on a novel construction of symmetry-based structured matrices -- to build approximately equivariant NNs with significantly reduced parameter counts. Our framework integrates the two aforementioned lines of work via the use of so-called Group Matrices (GMs), a forgotten precursor to the modern notion of regular representations of finite groups. GMs allow the design of structured matrices -- resembling LDR matrices -- which generalize the linear operations of a classical CNN from cyclic groups to general finite groups and their homogeneous spaces. We show that GMs can be employed to extend all the elementary operations of CNNs to general discrete groups. Further, the theory of structured matrices based on GMs provides a generalization of LDR theory focussed on matrices with cyclic structure, providing a tool for implementing approximate equivariance for discrete groups. We test GM-based architectures on a variety of tasks in the presence of relaxed symmetry. We report that our framework consistently performs competitively compared to approximately equivariant NNs, and other structured matrix-based compression frameworks, sometimes with a one or two orders of magnitude lower parameter count.