Shubhendu Trivedi
Recurrent Equivariant Constraint Modulation: Learning Per-Layer Symmetry Relaxation from Data
Feb 02, 2026Abstract:Equivariant neural networks exploit underlying task symmetries to improve generalization, but strict equivariance constraints can induce more complex optimization dynamics that can hinder learning. Prior work addresses these limitations by relaxing strict equivariance during training, but typically relies on prespecified, explicit, or implicit target levels of relaxation for each network layer, which are task-dependent and costly to tune. We propose Recurrent Equivariant Constraint Modulation (RECM), a layer-wise constraint modulation mechanism that learns appropriate relaxation levels solely from the training signal and the symmetry properties of each layer's input-target distribution, without requiring any prior knowledge about the task-dependent target relaxation level. We demonstrate that under the proposed RECM update, the relaxation level of each layer provably converges to a value upper-bounded by its symmetry gap, namely the degree to which its input-target distribution deviates from exact symmetry. Consequently, layers processing symmetric distributions recover full equivariance, while those with approximate symmetries retain sufficient flexibility to learn non-symmetric solutions when warranted by the data. Empirically, RECM outperforms prior methods across diverse exact and approximate equivariant tasks, including the challenging molecular conformer generation on the GEOM-Drugs dataset.
Watermarking Degrades Alignment in Language Models: Analysis and Mitigation
Jun 04, 2025Abstract:Watermarking techniques for large language models (LLMs) can significantly impact output quality, yet their effects on truthfulness, safety, and helpfulness remain critically underexamined. This paper presents a systematic analysis of how two popular watermarking approaches-Gumbel and KGW-affect these core alignment properties across four aligned LLMs. Our experiments reveal two distinct degradation patterns: guard attenuation, where enhanced helpfulness undermines model safety, and guard amplification, where excessive caution reduces model helpfulness. These patterns emerge from watermark-induced shifts in token distribution, surfacing the fundamental tension that exists between alignment objectives. To mitigate these degradations, we propose Alignment Resampling (AR), an inference-time sampling method that uses an external reward model to restore alignment. We establish a theoretical lower bound on the improvement in expected reward score as the sample size is increased and empirically demonstrate that sampling just 2-4 watermarked generations effectively recovers or surpasses baseline (unwatermarked) alignment scores. To overcome the limited response diversity of standard Gumbel watermarking, our modified implementation sacrifices strict distortion-freeness while maintaining robust detectability, ensuring compatibility with AR. Experimental results confirm that AR successfully recovers baseline alignment in both watermarking approaches, while maintaining strong watermark detectability. This work reveals the critical balance between watermark strength and model alignment, providing a simple inference-time solution to responsibly deploy watermarked LLMs in practice.
* Published at the 1st Workshop on GenAI Watermarking, collocated with ICLR 2025. OpenReview: https://openreview.net/forum?id=SIBkIV48gF
MCQA-Eval: Efficient Confidence Evaluation in NLG with Gold-Standard Correctness Labels
Feb 20, 2025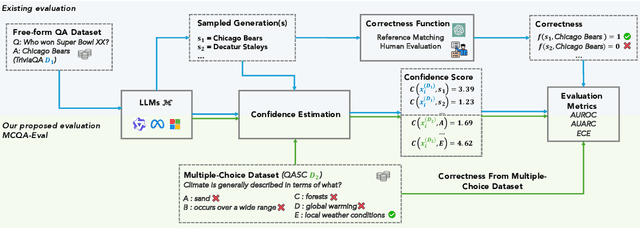

Abstract:Large Language Models (LLMs) require robust confidence estimation, particularly in critical domains like healthcare and law where unreliable outputs can lead to significant consequences. Despite much recent work in confidence estimation, current evaluation frameworks rely on correctness functions -- various heuristics that are often noisy, expensive, and possibly introduce systematic biases. These methodological weaknesses tend to distort evaluation metrics and thus the comparative ranking of confidence measures. We introduce MCQA-Eval, an evaluation framework for assessing confidence measures in Natural Language Generation (NLG) that eliminates dependence on an explicit correctness function by leveraging gold-standard correctness labels from multiple-choice datasets. MCQA-Eval enables systematic comparison of both internal state-based white-box (e.g. logit-based) and consistency-based black-box confidence measures, providing a unified evaluation methodology across different approaches. Through extensive experiments on multiple LLMs and widely used QA datasets, we report that MCQA-Eval provides efficient and more reliable assessments of confidence estimation methods than existing approaches.
Symmetry-Based Structured Matrices for Efficient Approximately Equivariant Networks
Sep 18, 2024Abstract:There has been much recent interest in designing symmetry-aware neural networks (NNs) exhibiting relaxed equivariance. Such NNs aim to interpolate between being exactly equivariant and being fully flexible, affording consistent performance benefits. In a separate line of work, certain structured parameter matrices -- those with displacement structure, characterized by low displacement rank (LDR) -- have been used to design small-footprint NNs. Displacement structure enables fast function and gradient evaluation, but permits accurate approximations via compression primarily to classical convolutional neural networks (CNNs). In this work, we propose a general framework -- based on a novel construction of symmetry-based structured matrices -- to build approximately equivariant NNs with significantly reduced parameter counts. Our framework integrates the two aforementioned lines of work via the use of so-called Group Matrices (GMs), a forgotten precursor to the modern notion of regular representations of finite groups. GMs allow the design of structured matrices -- resembling LDR matrices -- which generalize the linear operations of a classical CNN from cyclic groups to general finite groups and their homogeneous spaces. We show that GMs can be employed to extend all the elementary operations of CNNs to general discrete groups. Further, the theory of structured matrices based on GMs provides a generalization of LDR theory focussed on matrices with cyclic structure, providing a tool for implementing approximate equivariance for discrete groups. We test GM-based architectures on a variety of tasks in the presence of relaxed symmetry. We report that our framework consistently performs competitively compared to approximately equivariant NNs, and other structured matrix-based compression frameworks, sometimes with a one or two orders of magnitude lower parameter count.
Improving Equivariant Model Training via Constraint Relaxation
Aug 23, 2024



Abstract:Equivariant neural networks have been widely used in a variety of applications due to their ability to generalize well in tasks where the underlying data symmetries are known. Despite their successes, such networks can be difficult to optimize and require careful hyperparameter tuning to train successfully. In this work, we propose a novel framework for improving the optimization of such models by relaxing the hard equivariance constraint during training: We relax the equivariance constraint of the network's intermediate layers by introducing an additional non-equivariance term that we progressively constrain until we arrive at an equivariant solution. By controlling the magnitude of the activation of the additional relaxation term, we allow the model to optimize over a larger hypothesis space containing approximate equivariant networks and converge back to an equivariant solution at the end of training. We provide experimental results on different state-of-the-art network architectures, demonstrating how this training framework can result in equivariant models with improved generalization performance.
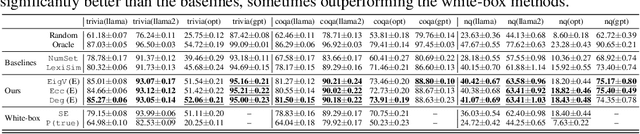
Contextualized Sequence Likelihood: Enhanced Confidence Scores for Natural Language Generation
Jun 03, 2024Abstract:The advent of large language models (LLMs) has dramatically advanced the state-of-the-art in numerous natural language generation tasks. For LLMs to be applied reliably, it is essential to have an accurate measure of their confidence. Currently, the most commonly used confidence score function is the likelihood of the generated sequence, which, however, conflates semantic and syntactic components. For instance, in question-answering (QA) tasks, an awkward phrasing of the correct answer might result in a lower probability prediction. Additionally, different tokens should be weighted differently depending on the context. In this work, we propose enhancing the predicted sequence probability by assigning different weights to various tokens using attention values elicited from the base LLM. By employing a validation set, we can identify the relevant attention heads, thereby significantly improving the reliability of the vanilla sequence probability confidence measure. We refer to this new score as the Contextualized Sequence Likelihood (CSL). CSL is easy to implement, fast to compute, and offers considerable potential for further improvement with task-specific prompts. Across several QA datasets and a diverse array of LLMs, CSL has demonstrated significantly higher reliability than state-of-the-art baselines in predicting generation quality, as measured by the AUROC or AUARC.
Position Paper: Generalized grammar rules and structure-based generalization beyond classical equivariance for lexical tasks and transduction
Feb 02, 2024Abstract:Compositional generalization is one of the main properties which differentiates lexical learning in humans from state-of-art neural networks. We propose a general framework for building models that can generalize compositionally using the concept of Generalized Grammar Rules (GGRs), a class of symmetry-based compositional constraints for transduction tasks, which we view as a transduction analogue of equivariance constraints in physics-inspired tasks. Besides formalizing generalized notions of symmetry for language transduction, our framework is general enough to contain many existing works as special cases. We present ideas on how GGRs might be implemented, and in the process draw connections to reinforcement learning and other areas of research.
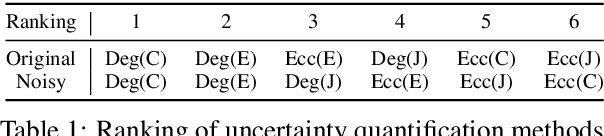
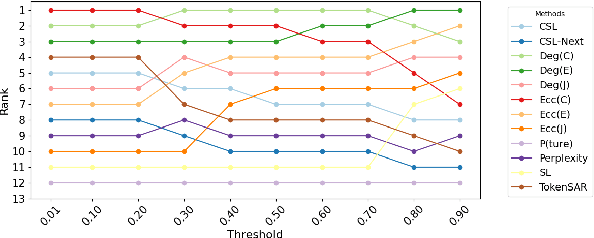
Generating with Confidence: Uncertainty Quantification for Black-box Large Language Models
May 30, 2023
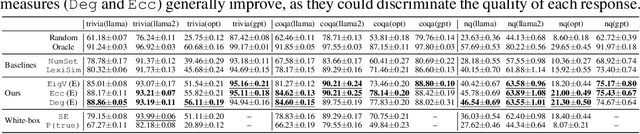
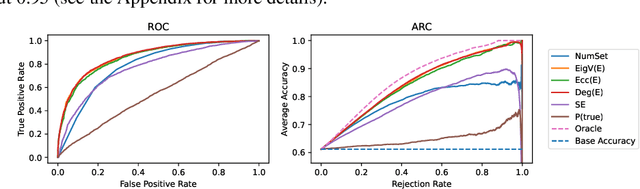
Abstract:Large language models (LLMs) specializing in natural language generation (NLG) have recently started exhibiting promising capabilities across a variety of domains. However, gauging the trustworthiness of responses generated by LLMs remains an open challenge, with limited research on uncertainty quantification for NLG. Furthermore, existing literature typically assumes white-box access to language models, which is becoming unrealistic either due to the closed-source nature of the latest LLMs or due to computational constraints. In this work, we investigate uncertainty quantification in NLG for $\textit{black-box}$ LLMs. We first differentiate two closely-related notions: $\textit{uncertainty}$, which depends only on the input, and $\textit{confidence}$, which additionally depends on the generated response. We then propose and compare several confidence/uncertainty metrics, applying them to $\textit{selective NLG}$, where unreliable results could either be ignored or yielded for further assessment. Our findings on several popular LLMs and datasets reveal that a simple yet effective metric for the average semantic dispersion can be a reliable predictor of the quality of LLM responses. This study can provide valuable insights for practitioners on uncertainty management when adopting LLMs. The code to replicate all our experiments is available at https://github.com/zlin7/UQ-NLG.
Approximation-Generalization Trade-offs under (Approximate) Group Equivariance
May 27, 2023Abstract:The explicit incorporation of task-specific inductive biases through symmetry has emerged as a general design precept in the development of high-performance machine learning models. For example, group equivariant neural networks have demonstrated impressive performance across various domains and applications such as protein and drug design. A prevalent intuition about such models is that the integration of relevant symmetry results in enhanced generalization. Moreover, it is posited that when the data and/or the model may only exhibit $\textit{approximate}$ or $\textit{partial}$ symmetry, the optimal or best-performing model is one where the model symmetry aligns with the data symmetry. In this paper, we conduct a formal unified investigation of these intuitions. To begin, we present general quantitative bounds that demonstrate how models capturing task-specific symmetries lead to improved generalization. In fact, our results do not require the transformations to be finite or even form a group and can work with partial or approximate equivariance. Utilizing this quantification, we examine the more general question of model mis-specification i.e. when the model symmetries don't align with the data symmetries. We establish, for a given symmetry group, a quantitative comparison between the approximate/partial equivariance of the model and that of the data distribution, precisely connecting model equivariance error and data equivariance error. Our result delineates conditions under which the model equivariance error is optimal, thereby yielding the best-performing model for the given task and data.
Fast Online Value-Maximizing Prediction Sets with Conformal Cost Control
Feb 02, 2023Abstract:Many real-world multi-label prediction problems involve set-valued predictions that must satisfy specific requirements dictated by downstream usage. We focus on a typical scenario where such requirements, separately encoding \textit{value} and \textit{cost}, compete with each other. For instance, a hospital might expect a smart diagnosis system to capture as many severe, often co-morbid, diseases as possible (the value), while maintaining strict control over incorrect predictions (the cost). We present a general pipeline, dubbed as FavMac, to maximize the value while controlling the cost in such scenarios. FavMac can be combined with almost any multi-label classifier, affording distribution-free theoretical guarantees on cost control. Moreover, unlike prior works, FavMac can handle real-world large-scale applications via a carefully designed online update mechanism, which is of independent interest. Our methodological and theoretical contributions are supported by experiments on several healthcare tasks and synthetic datasets - FavMac furnishes higher value compared with several variants and baselines while maintaining strict cost control.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge