Neural Inertial Odometry from Lie Events

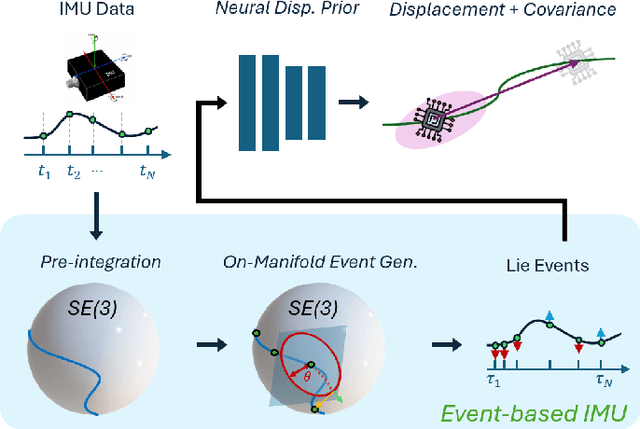
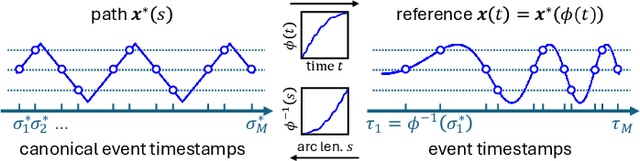
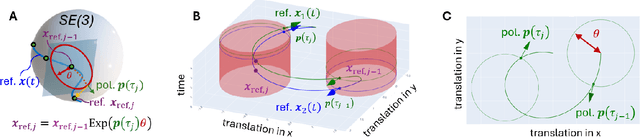
Neural displacement priors (NDP) can reduce the drift in inertial odometry and provide uncertainty estimates that can be readily fused with off-the-shelf filters. However, they fail to generalize to different IMU sampling rates and trajectory profiles, which limits their robustness in diverse settings. To address this challenge, we replace the traditional NDP inputs comprising raw IMU data with Lie events that are robust to input rate changes and have favorable invariances when observed under different trajectory profiles. Unlike raw IMU data sampled at fixed rates, Lie events are sampled whenever the norm of the IMU pre-integration change, mapped to the Lie algebra of the SE(3) group, exceeds a threshold. Inspired by event-based vision, we generalize the notion of level-crossing on 1D signals to level-crossings on the Lie algebra and generalize binary polarities to normalized Lie polarities within this algebra. We show that training NDPs on Lie events incorporating these polarities reduces the trajectory error of off-the-shelf downstream inertial odometry methods by up to 21% with only minimal preprocessing. We conjecture that many more sensors than IMUs or cameras can benefit from an event-based sampling paradigm and that this work makes an important first step in this direction.

Improving Equivariant Model Training via Constraint Relaxation

Equivariant neural networks have been widely used in a variety of applications due to their ability to generalize well in tasks where the underlying data symmetries are known. Despite their successes, such networks can be difficult to optimize and require careful hyperparameter tuning to train successfully. In this work, we propose a novel framework for improving the optimization of such models by relaxing the hard equivariance constraint during training: We relax the equivariance constraint of the network's intermediate layers by introducing an additional non-equivariance term that we progressively constrain until we arrive at an equivariant solution. By controlling the magnitude of the activation of the additional relaxation term, we allow the model to optimize over a larger hypothesis space containing approximate equivariant networks and converge back to an equivariant solution at the end of training. We provide experimental results on different state-of-the-art network architectures, demonstrating how this training framework can result in equivariant models with improved generalization performance.

EqNIO: Subequivariant Neural Inertial Odometry

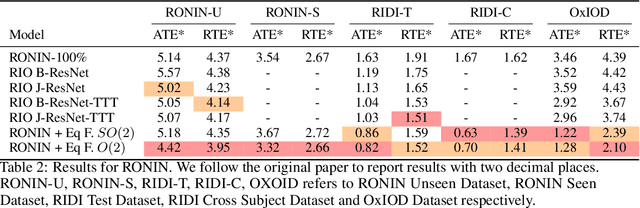
Presently, neural networks are widely employed to accurately estimate 2D displacements and associated uncertainties from Inertial Measurement Unit (IMU) data that can be integrated into stochastic filter networks like the Extended Kalman Filter (EKF) as measurements and uncertainties for the update step in the filter. However, such neural approaches overlook symmetry which is a crucial inductive bias for model generalization. This oversight is notable because (i) physical laws adhere to symmetry principles when considering the gravity axis, meaning there exists the same transformation for both the physical entity and the resulting trajectory, and (ii) displacements should remain equivariant to frame transformations when the inertial frame changes. To address this, we propose a subequivariant framework by: (i) deriving fundamental layers such as linear and nonlinear layers for a subequivariant network, designed to handle sequences of vectors and scalars, (ii) employing the subequivariant network to predict an equivariant frame for the sequence of inertial measurements. This predicted frame can then be utilized for extracting invariant features through projection, which are integrated with arbitrary network architectures, (iii) transforming the invariant output by frame transformation to obtain equivariant displacements and covariances. We demonstrate the effectiveness and generalization of our Equivariant Framework on a filter-based approach with TLIO architecture for TLIO and Aria datasets, and an end-to-end deep learning approach with RONIN architecture for RONIN, RIDI and OxIOD datasets.

BiEquiFormer: Bi-Equivariant Representations for Global Point Cloud Registration

The goal of this paper is to address the problem of \textit{global} point cloud registration (PCR) i.e., finding the optimal alignment between point clouds irrespective of the initial poses of the scans. This problem is notoriously challenging for classical optimization methods due to computational constraints. First, we show that state-of-the-art deep learning methods suffer from huge performance degradation when the point clouds are arbitrarily placed in space. We propose that \textit{equivariant deep learning} should be utilized for solving this task and we characterize the specific type of bi-equivariance of PCR. Then, we design BiEquiformer a novel and scalable \textit{bi-equivariant} pipeline i.e. equivariant to the independent transformations of the input point clouds. While a naive approach would process the point clouds independently we design expressive bi-equivariant layers that fuse the information from both point clouds. This allows us to extract high-quality superpoint correspondences and in turn, robust point-cloud registration. Extensive comparisons against state-of-the-art methods show that our method achieves comparable performance in the canonical setting and superior performance in the robust setting in both the 3DMatch and the challenging low-overlap 3DLoMatch dataset.

Graph Neural Networks for Multi-Robot Active Information Acquisition

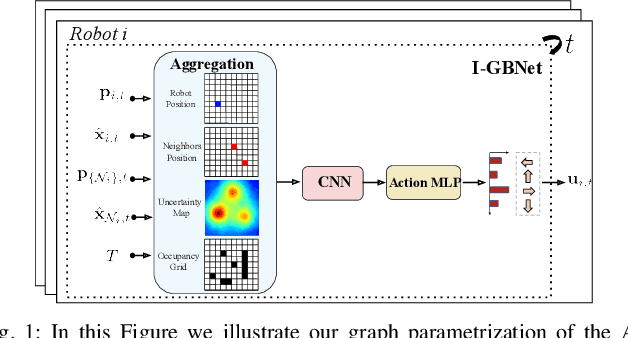
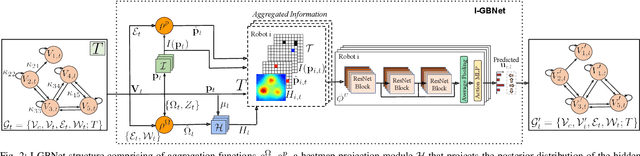
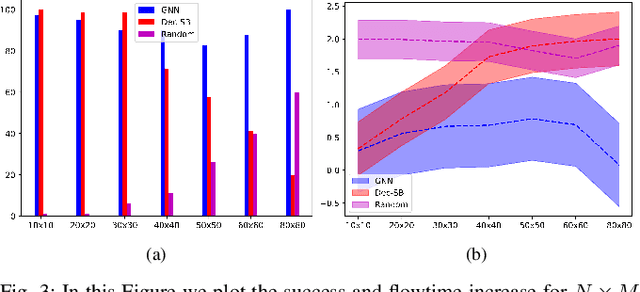
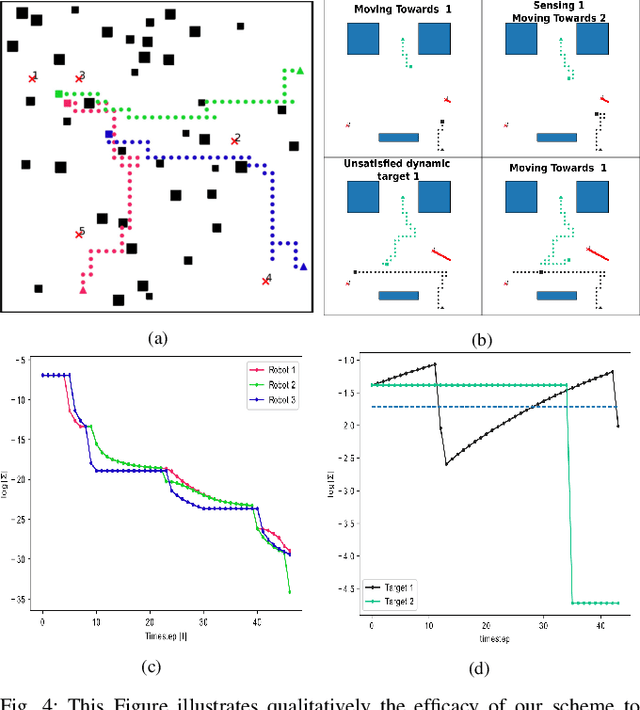
This paper addresses the Multi-Robot Active Information Acquisition (AIA) problem, where a team of mobile robots, communicating through an underlying graph, estimates a hidden state expressing a phenomenon of interest. Applications like target tracking, coverage and SLAM can be expressed in this framework. Existing approaches, though, are either not scalable, unable to handle dynamic phenomena or not robust to changes in the communication graph. To counter these shortcomings, we propose an Information-aware Graph Block Network (I-GBNet), an AIA adaptation of Graph Neural Networks, that aggregates information over the graph representation and provides sequential-decision making in a distributed manner. The I-GBNet, trained via imitation learning with a centralized sampling-based expert solver, exhibits permutation equivariance and time invariance, while harnessing the superior scalability, robustness and generalizability to previously unseen environments and robot configurations. Experiments on significantly larger graphs and dimensionality of the hidden state and more complex environments than those seen in training validate the properties of the proposed architecture and its efficacy in the application of localization and tracking of dynamic targets.

SE(3)-Equivariant Attention Networks for Shape Reconstruction in Function Space

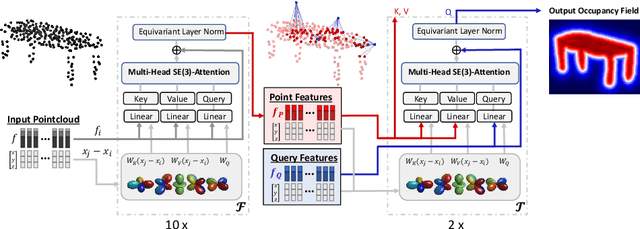
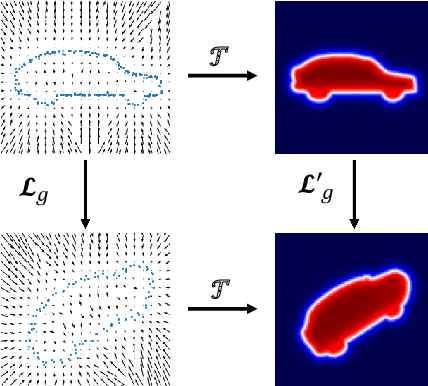
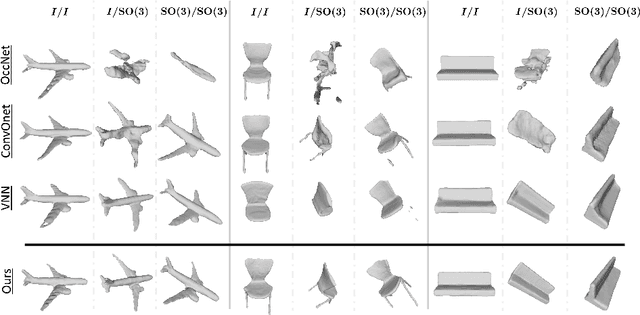
We propose the first SE(3)-equivariant coordinate-based network for learning occupancy fields from point clouds. In contrast to previous shape reconstruction methods that align the input to a regular grid, we operate directly on the irregular, unoriented point cloud. We leverage attention mechanisms in order to preserve the set structure (permutation equivariance and variable length) of the input. At the same time, attention layers enable local shape modelling, a crucial property for scalability to large scenes. In contrast to architectures that create a global signature for the shape, we operate on local tokens. Given an unoriented, sparse, noisy point cloud as input, we produce equivariant features for each point. These serve as keys and values for the subsequent equivariant cross-attention blocks that parametrize the occupancy field. By querying an arbitrary point in space, we predict its occupancy score. We show that our method outperforms previous SO(3)-equivariant methods, as well as non-equivariant methods trained on SO(3)-augmented datasets. More importantly, local modelling together with SE(3)-equivariance create an ideal setting for SE(3) scene reconstruction. We show that by training only on single objects and without any pre-segmentation, we can reconstruct a novel scene with single-object performance.

Learning Augmentation Distributions using Transformed Risk Minimization

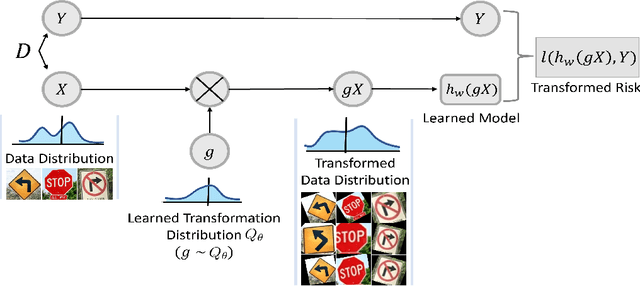
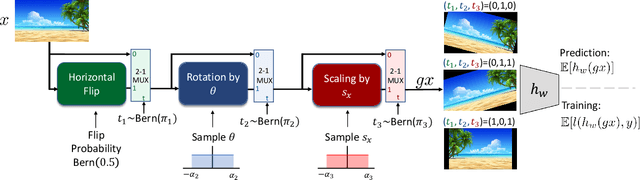
Adapting to the structure of data distributions (such as symmetry and transformation invariances) is an important challenge in machine learning. Invariances can be built into the learning process by architecture design, or by augmenting the dataset. Both require a priori knowledge about the exact nature of the symmetries. Absent this knowledge, practitioners resort to expensive and time-consuming tuning. To address this problem, we propose a new approach to learn distributions of augmentation transforms, in a new \emph{Transformed Risk Minimization} (TRM) framework. In addition to predictive models, we also optimize over transformations chosen from a hypothesis space. As an algorithmic framework, our TRM method is (1) efficient (jointly learns augmentations and models in a \emph{single training loop}), (2) modular (works with \emph{any} training algorithm), and (3) general (handles \emph{both discrete and continuous} augmentations). We theoretically compare TRM with standard risk minimization, and give a PAC-Bayes upper bound on its generalization error. We propose to optimize this bound over a rich augmentation space via a new parametrization over compositions of blocks, leading to the new \emph{Stochastic Compositional Augmentation Learning} (SCALE) algorithm. We compare SCALE experimentally with prior methods (Fast AutoAugment and Augerino) on CIFAR10/100, SVHN . Additionally, we show that SCALE can correctly learn certain symmetries in the data distribution (recovering rotations on rotated MNIST) and can also improve calibration of the learned model.