EqNIO: Subequivariant Neural Inertial Odometry
Paper and Code
Aug 12, 2024


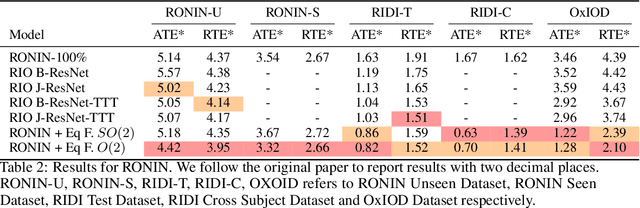
Presently, neural networks are widely employed to accurately estimate 2D displacements and associated uncertainties from Inertial Measurement Unit (IMU) data that can be integrated into stochastic filter networks like the Extended Kalman Filter (EKF) as measurements and uncertainties for the update step in the filter. However, such neural approaches overlook symmetry which is a crucial inductive bias for model generalization. This oversight is notable because (i) physical laws adhere to symmetry principles when considering the gravity axis, meaning there exists the same transformation for both the physical entity and the resulting trajectory, and (ii) displacements should remain equivariant to frame transformations when the inertial frame changes. To address this, we propose a subequivariant framework by: (i) deriving fundamental layers such as linear and nonlinear layers for a subequivariant network, designed to handle sequences of vectors and scalars, (ii) employing the subequivariant network to predict an equivariant frame for the sequence of inertial measurements. This predicted frame can then be utilized for extracting invariant features through projection, which are integrated with arbitrary network architectures, (iii) transforming the invariant output by frame transformation to obtain equivariant displacements and covariances. We demonstrate the effectiveness and generalization of our Equivariant Framework on a filter-based approach with TLIO architecture for TLIO and Aria datasets, and an end-to-end deep learning approach with RONIN architecture for RONIN, RIDI and OxIOD datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge