Yinshuang Xu
Neural Inertial Odometry from Lie Events
May 14, 2025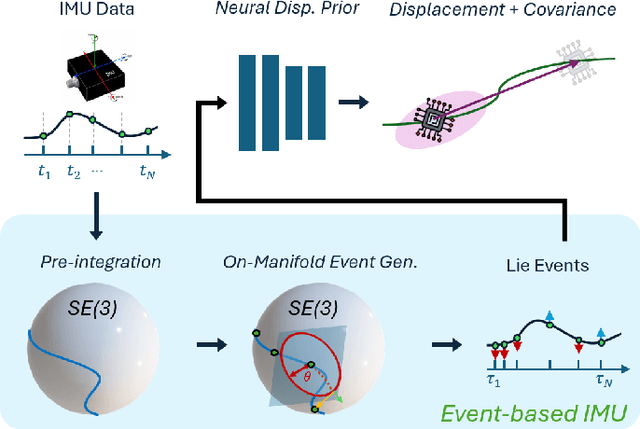
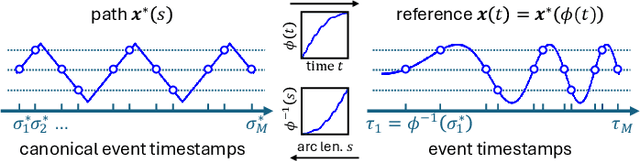
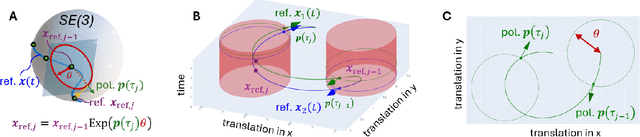

Abstract:Neural displacement priors (NDP) can reduce the drift in inertial odometry and provide uncertainty estimates that can be readily fused with off-the-shelf filters. However, they fail to generalize to different IMU sampling rates and trajectory profiles, which limits their robustness in diverse settings. To address this challenge, we replace the traditional NDP inputs comprising raw IMU data with Lie events that are robust to input rate changes and have favorable invariances when observed under different trajectory profiles. Unlike raw IMU data sampled at fixed rates, Lie events are sampled whenever the norm of the IMU pre-integration change, mapped to the Lie algebra of the SE(3) group, exceeds a threshold. Inspired by event-based vision, we generalize the notion of level-crossing on 1D signals to level-crossings on the Lie algebra and generalize binary polarities to normalized Lie polarities within this algebra. We show that training NDPs on Lie events incorporating these polarities reduces the trajectory error of off-the-shelf downstream inertial odometry methods by up to 21% with only minimal preprocessing. We conjecture that many more sensors than IMUs or cameras can benefit from an event-based sampling paradigm and that this work makes an important first step in this direction.
$SE(3)$ Equivariant Ray Embeddings for Implicit Multi-View Depth Estimation
Nov 11, 2024Abstract:Incorporating inductive bias by embedding geometric entities (such as rays) as input has proven successful in multi-view learning. However, the methods adopting this technique typically lack equivariance, which is crucial for effective 3D learning. Equivariance serves as a valuable inductive prior, aiding in the generation of robust multi-view features for 3D scene understanding. In this paper, we explore the application of equivariant multi-view learning to depth estimation, not only recognizing its significance for computer vision and robotics but also addressing the limitations of previous research. Most prior studies have either overlooked equivariance in this setting or achieved only approximate equivariance through data augmentation, which often leads to inconsistencies across different reference frames. To address this issue, we propose to embed $SE(3)$ equivariance into the Perceiver IO architecture. We employ Spherical Harmonics for positional encoding to ensure 3D rotation equivariance, and develop a specialized equivariant encoder and decoder within the Perceiver IO architecture. To validate our model, we applied it to the task of stereo depth estimation, achieving state of the art results on real-world datasets without explicit geometric constraints or extensive data augmentation.
EqNIO: Subequivariant Neural Inertial Odometry
Aug 12, 2024


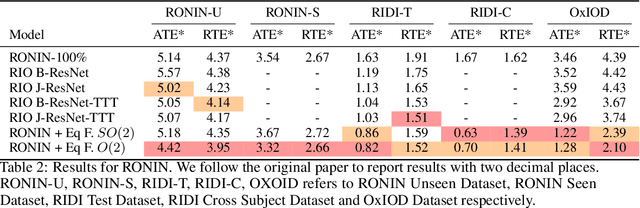
Abstract:Presently, neural networks are widely employed to accurately estimate 2D displacements and associated uncertainties from Inertial Measurement Unit (IMU) data that can be integrated into stochastic filter networks like the Extended Kalman Filter (EKF) as measurements and uncertainties for the update step in the filter. However, such neural approaches overlook symmetry which is a crucial inductive bias for model generalization. This oversight is notable because (i) physical laws adhere to symmetry principles when considering the gravity axis, meaning there exists the same transformation for both the physical entity and the resulting trajectory, and (ii) displacements should remain equivariant to frame transformations when the inertial frame changes. To address this, we propose a subequivariant framework by: (i) deriving fundamental layers such as linear and nonlinear layers for a subequivariant network, designed to handle sequences of vectors and scalars, (ii) employing the subequivariant network to predict an equivariant frame for the sequence of inertial measurements. This predicted frame can then be utilized for extracting invariant features through projection, which are integrated with arbitrary network architectures, (iii) transforming the invariant output by frame transformation to obtain equivariant displacements and covariances. We demonstrate the effectiveness and generalization of our Equivariant Framework on a filter-based approach with TLIO architecture for TLIO and Aria datasets, and an end-to-end deep learning approach with RONIN architecture for RONIN, RIDI and OxIOD datasets.
SE(3)-Equivariant Reconstruction from Light Field
Dec 30, 2022
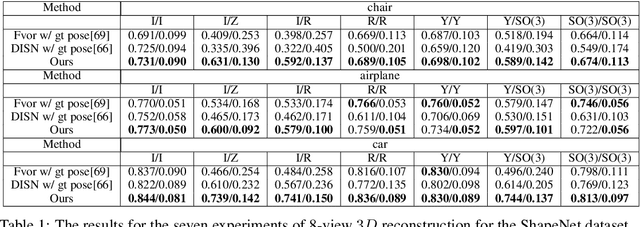
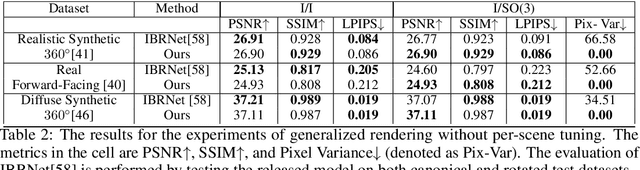
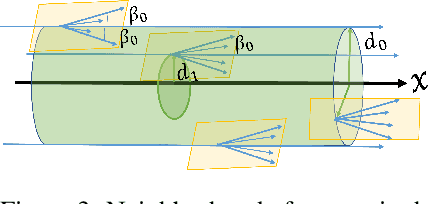
Abstract:Recent progress in geometric computer vision has shown significant advances in reconstruction and novel view rendering from multiple views by capturing the scene as a neural radiance field. Such approaches have changed the paradigm of reconstruction but need a plethora of views and do not make use of object shape priors. On the other hand, deep learning has shown how to use priors in order to infer shape from single images. Such approaches, though, require that the object is reconstructed in a canonical pose or assume that object pose is known during training. In this paper, we address the problem of how to compute equivariant priors for reconstruction from a few images, given the relative poses of the cameras. Our proposed reconstruction is $SE(3)$-gauge equivariant, meaning that it is equivariant to the choice of world frame. To achieve this, we make two novel contributions to light field processing: we define light field convolution and we show how it can be approximated by intra-view $SE(2)$ convolutions because the original light field convolution is computationally and memory-wise intractable; we design a map from the light field to $\mathbb{R}^3$ that is equivariant to the transformation of the world frame and to the rotation of the views. We demonstrate equivariance by obtaining robust results in roto-translated datasets without performing transformation augmentation.
Unified Fourier-based Kernel and Nonlinearity Design for Equivariant Networks on Homogeneous Spaces
Jun 19, 2022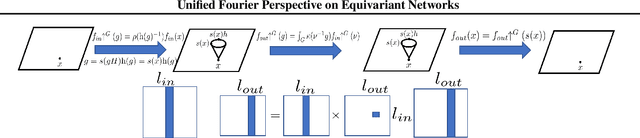
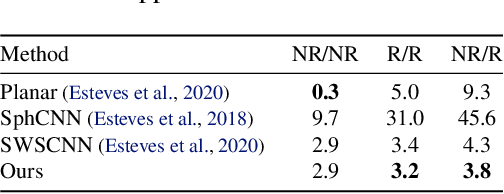

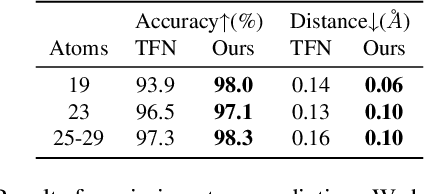
Abstract:We introduce a unified framework for group equivariant networks on homogeneous spaces derived from a Fourier perspective. We consider tensor-valued feature fields, before and after a convolutional layer. We present a unified derivation of kernels via the Fourier domain by leveraging the sparsity of Fourier coefficients of the lifted feature fields. The sparsity emerges when the stabilizer subgroup of the homogeneous space is a compact Lie group. We further introduce a nonlinear activation, via an elementwise nonlinearity on the regular representation after lifting and projecting back to the field through an equivariant convolution. We show that other methods treating features as the Fourier coefficients in the stabilizer subgroup are special cases of our activation. Experiments on $SO(3)$ and $SE(3)$ show state-of-the-art performance in spherical vector field regression, point cloud classification, and molecular completion.
Nested Scale Editing for Conditional Image Synthesis
Jun 03, 2020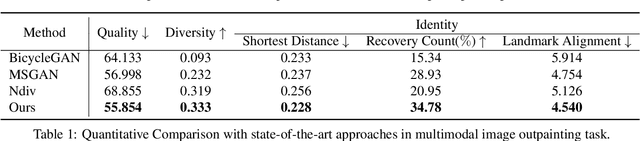
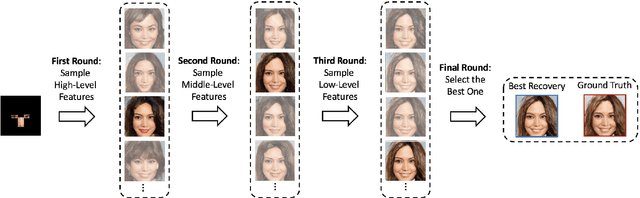
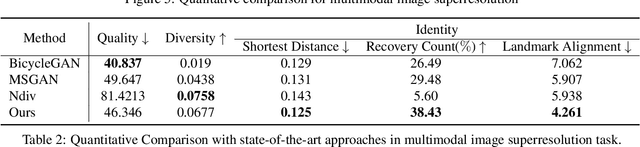
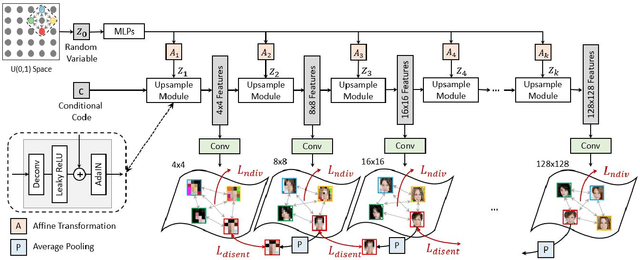
Abstract:We propose an image synthesis approach that provides stratified navigation in the latent code space. With a tiny amount of partial or very low-resolution image, our approach can consistently out-perform state-of-the-art counterparts in terms of generating the closest sampled image to the ground truth. We achieve this through scale-independent editing while expanding scale-specific diversity. Scale-independence is achieved with a nested scale disentanglement loss. Scale-specific diversity is created by incorporating a progressive diversification constraint. We introduce semantic persistency across the scales by sharing common latent codes. Together they provide better control of the image synthesis process. We evaluate the effectiveness of our proposed approach through various tasks, including image outpainting, image superresolution, and cross-domain image translation.
Equivariant Multi-View Networks
Apr 01, 2019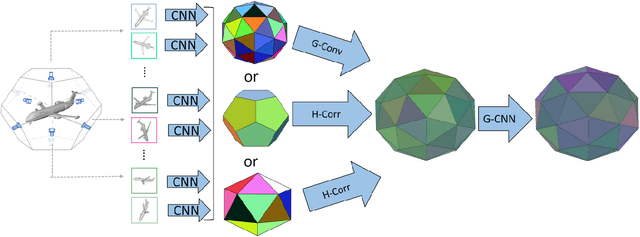
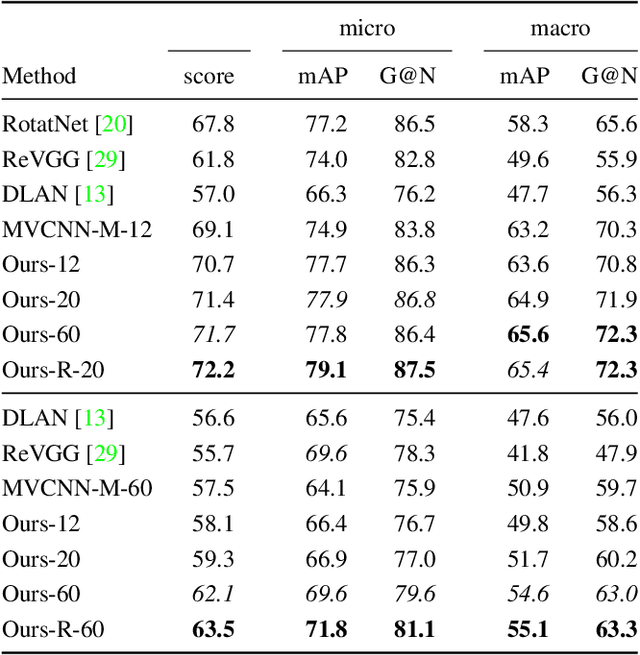

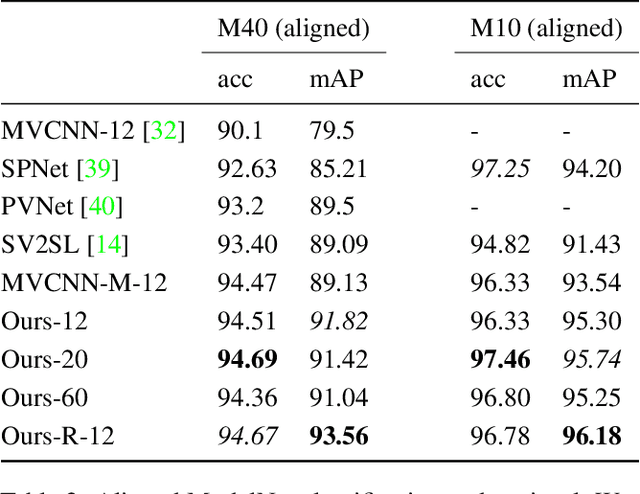
Abstract:Several approaches to 3D vision tasks process multiple views of the input independently with deep neural networks pre-trained on natural images, achieving view permutation invariance through a single round of pooling over all views. We argue that this operation discards important information and leads to subpar global descriptors. In this paper, we propose a group convolutional approach to multiple view aggregation where convolutions are performed over a discrete subgroup of the rotation group, enabling, thus, joint reasoning over all views in an equivariant (instead of invariant) fashion, up to the very last layer. We further develop this idea to operate on smaller discrete homogeneous spaces of the rotation group, where a polar view representation is used to maintain equivariance with only a fraction of the number of input views. We set the new state of the art in several large scale 3D shape retrieval tasks, and show additional applications to panoramic scene classification.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge