SE(3)-Equivariant Reconstruction from Light Field

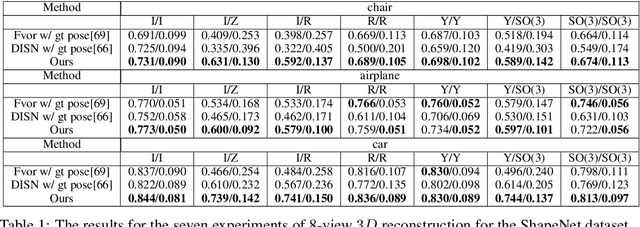
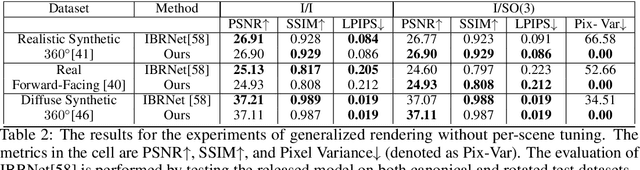
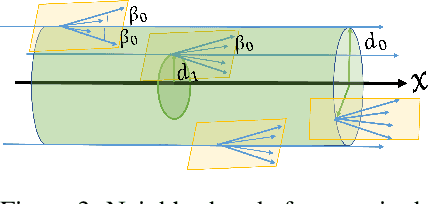
Recent progress in geometric computer vision has shown significant advances in reconstruction and novel view rendering from multiple views by capturing the scene as a neural radiance field. Such approaches have changed the paradigm of reconstruction but need a plethora of views and do not make use of object shape priors. On the other hand, deep learning has shown how to use priors in order to infer shape from single images. Such approaches, though, require that the object is reconstructed in a canonical pose or assume that object pose is known during training. In this paper, we address the problem of how to compute equivariant priors for reconstruction from a few images, given the relative poses of the cameras. Our proposed reconstruction is $SE(3)$-gauge equivariant, meaning that it is equivariant to the choice of world frame. To achieve this, we make two novel contributions to light field processing: we define light field convolution and we show how it can be approximated by intra-view $SE(2)$ convolutions because the original light field convolution is computationally and memory-wise intractable; we design a map from the light field to $\mathbb{R}^3$ that is equivariant to the transformation of the world frame and to the rotation of the views. We demonstrate equivariance by obtaining robust results in roto-translated datasets without performing transformation augmentation.