Surrogate Modeling of 3D Rayleigh-Benard Convection with Equivariant Autoencoders

The use of machine learning for modeling, understanding, and controlling large-scale physics systems is quickly gaining in popularity, with examples ranging from electromagnetism over nuclear fusion reactors and magneto-hydrodynamics to fluid mechanics and climate modeling. These systems -- governed by partial differential equations -- present unique challenges regarding the large number of degrees of freedom and the complex dynamics over many scales both in space and time, and additional measures to improve accuracy and sample efficiency are highly desirable. We present an end-to-end equivariant surrogate model consisting of an equivariant convolutional autoencoder and an equivariant convolutional LSTM using $G$-steerable kernels. As a case study, we consider the three-dimensional Rayleigh-B\'enard convection, which describes the buoyancy-driven fluid flow between a heated bottom and a cooled top plate. While the system is E(2)-equivariant in the horizontal plane, the boundary conditions break the translational equivariance in the vertical direction. Our architecture leverages vertically stacked layers of $D_4$-steerable kernels, with additional partial kernel sharing in the vertical direction for further efficiency improvement. Our results demonstrate significant gains both in sample and parameter efficiency, as well as a better scaling to more complex dynamics, that is, larger Rayleigh numbers. The accompanying code is available under https://github.com/FynnFromme/equivariant-rb-forecasting.

GAGrasp: Geometric Algebra Diffusion for Dexterous Grasping

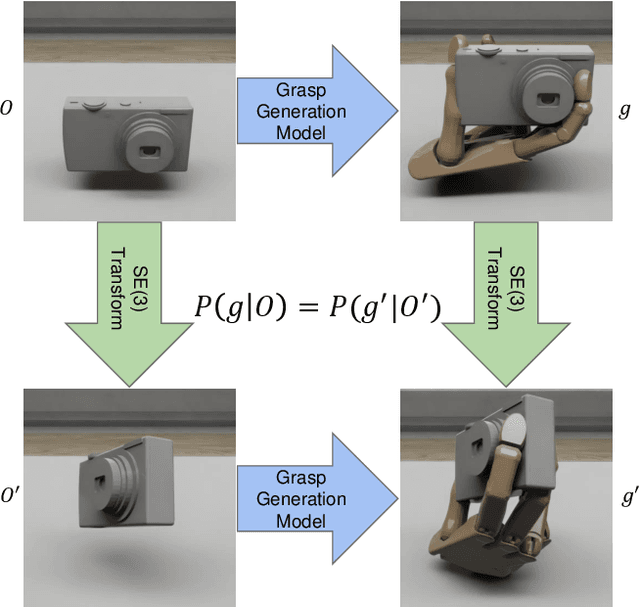
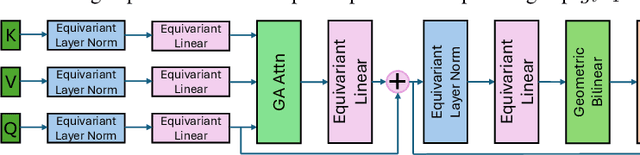
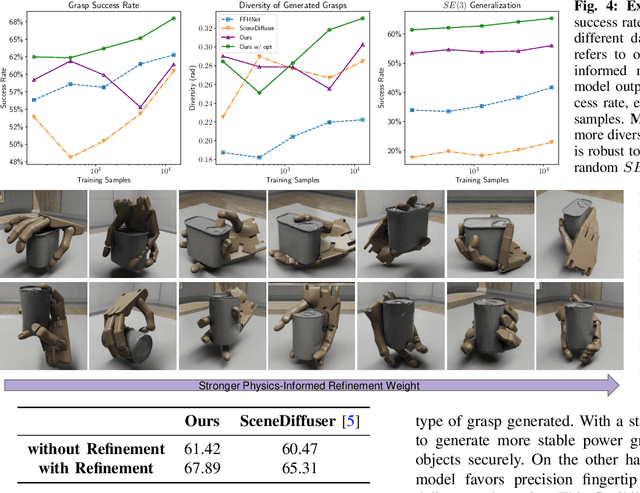
We propose GAGrasp, a novel framework for dexterous grasp generation that leverages geometric algebra representations to enforce equivariance to SE(3) transformations. By encoding the SE(3) symmetry constraint directly into the architecture, our method improves data and parameter efficiency while enabling robust grasp generation across diverse object poses. Additionally, we incorporate a differentiable physics-informed refinement layer, which ensures that generated grasps are physically plausible and stable. Extensive experiments demonstrate the model's superior performance in generalization, stability, and adaptability compared to existing methods. Additional details at https://gagrasp.github.io/

Understanding Oversmoothing in GNNs as Consensus in Opinion Dynamics

In contrast to classes of neural networks where the learned representations become increasingly expressive with network depth, the learned representations in graph neural networks (GNNs), tend to become increasingly similar. This phenomena, known as oversmoothing, is characterized by learned representations that cannot be reliably differentiated leading to reduced predictive performance. In this paper, we propose an analogy between oversmoothing in GNNs and consensus or agreement in opinion dynamics. Through this analogy, we show that the message passing structure of recent continuous-depth GNNs is equivalent to a special case of opinion dynamics (i.e., linear consensus models) which has been theoretically proven to converge to consensus (i.e., oversmoothing) for all inputs. Using the understanding developed through this analogy, we design a new continuous-depth GNN model based on nonlinear opinion dynamics and prove that our model, which we call behavior-inspired message passing neural network (BIMP) circumvents oversmoothing for general inputs. Through extensive experiments, we show that BIMP is robust to oversmoothing and adversarial attack, and consistently outperforms competitive baselines on numerous benchmarks.

Relational Reasoning On Graphs Using Opinion Dynamics

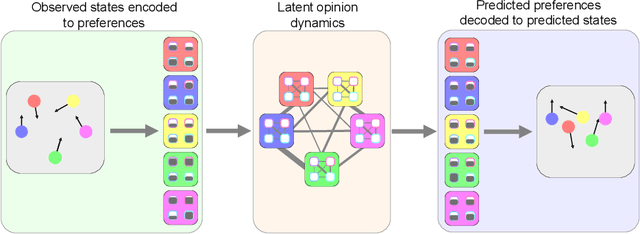
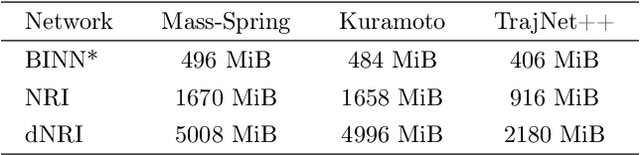
From pedestrians to Kuramoto oscillators, interactions between agents govern how a multitude of dynamical systems evolve in space and time. Discovering how these agents relate to each other can improve our understanding of the often complex dynamics that underlie these systems. Recent works learn to categorize relationships between agents based on observations of their physical behavior. These approaches are limited in that the relationship categories are modelled as independent and mutually exclusive, when in real world systems categories are often interacting. In this work, we introduce a level of abstraction between the physical behavior of agents and the categories that define their behavior. To do this, we learn a mapping from the agents' states to their affinities for each category in a graph neural network. We integrate the physical proximity of agents and their affinities in a nonlinear opinion dynamics model which provides a mechanism to identify mutually exclusive categories, predict an agent's evolution in time, and control an agent's behavior. We demonstrate the utility of our model for learning interpretable categories for mechanical systems, and demonstrate its efficacy on several long-horizon trajectory prediction benchmarks where we consistently out perform existing methods.

Color Equivariant Network

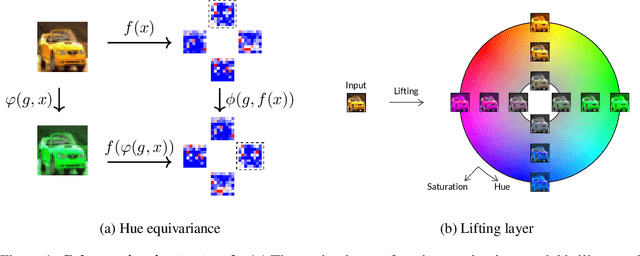
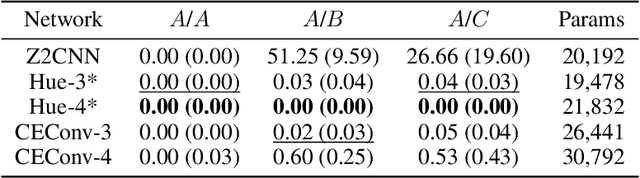
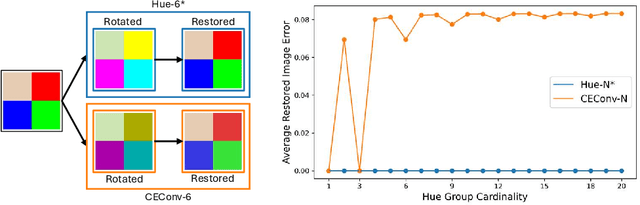
Group equivariant convolutional neural networks have been designed for a variety of geometric transformations from 2D and 3D rotation groups, to semi-groups such as scale. Despite the improved interpretability, accuracy and generalizability afforded by these architectures, group equivariant networks have seen limited application in the context of perceptual quantities such as hue and saturation, even though their variation can lead to significant reductions in classification performance. In this paper, we introduce convolutional neural networks equivariant to variations in hue and saturation by design. To achieve this, we leverage the observation that hue and saturation transformations can be identified with the 2D rotation and 1D translation groups respectively. Our hue-, saturation-, and fully color-equivariant networks achieve equivariance to these perceptual transformations without an increase in network parameters. We demonstrate the utility of our networks on synthetic and real world datasets where color and lighting variations are commonplace.

Learning to predict 3D rotational dynamics from images of a rigid body with unknown mass distribution

In many real-world settings, image observations of freely rotating 3D rigid bodies, may be available when low-dimensional measurements are not. However, the high-dimensionality of image data precludes the use of classical estimation techniques to learn the dynamics. The usefulness of standard deep learning methods is also limited because an image of a rigid body reveals nothing about the distribution of mass inside the body, which, together with initial angular velocity, is what determines how the body will rotate. We present a physics-informed neural network model to estimate and predict 3D rotational dynamics from image sequences. We achieve this using a multi-stage prediction pipeline that maps individual images to a latent representation homeomorphic to $\mathbf{SO}(3)$, computes angular velocities from latent pairs, and predicts future latent states using the Hamiltonian equations of motion. We demonstrate the efficacy of our approach on new rotating rigid-body datasets of sequences of synthetic images of rotating objects, including cubes, prisms and satellites, with unknown uniform and non-uniform mass distributions.

Hamiltonian GAN

A growing body of work leverages the Hamiltonian formalism as an inductive bias for physically plausible neural network based video generation. The structure of the Hamiltonian ensures conservation of a learned quantity (e.g., energy) and imposes a phase-space interpretation on the low-dimensional manifold underlying the input video. While this interpretation has the potential to facilitate the integration of learned representations in downstream tasks, existing methods are limited in their applicability as they require a structural prior for the configuration space at design time. In this work, we present a GAN-based video generation pipeline with a learned configuration space map and Hamiltonian neural network motion model, to learn a representation of the configuration space from data. We train our model with a physics-inspired cyclic-coordinate loss function which encourages a minimal representation of the configuration space and improves interpretability. We demonstrate the efficacy and advantages of our approach on the Hamiltonian Dynamics Suite Toy Physics dataset.

Learning Interpretable Dynamics from Images of a Freely Rotating 3D Rigid Body

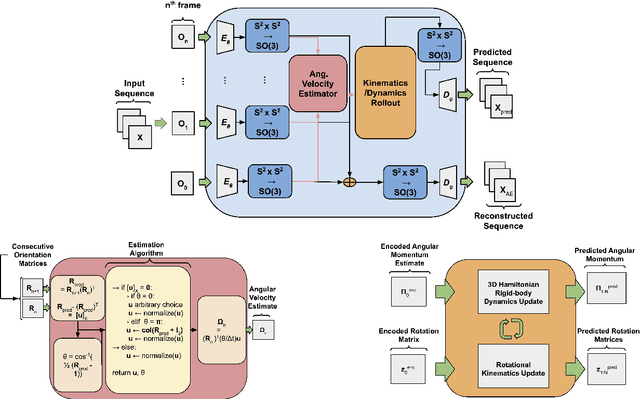
In many real-world settings, image observations of freely rotating 3D rigid bodies, such as satellites, may be available when low-dimensional measurements are not. However, the high-dimensionality of image data precludes the use of classical estimation techniques to learn the dynamics and a lack of interpretability reduces the usefulness of standard deep learning methods. In this work, we present a physics-informed neural network model to estimate and predict 3D rotational dynamics from image sequences. We achieve this using a multi-stage prediction pipeline that maps individual images to a latent representation homeomorphic to $\mathbf{SO}(3)$, computes angular velocities from latent pairs, and predicts future latent states using the Hamiltonian equations of motion with a learned representation of the Hamiltonian. We demonstrate the efficacy of our approach on a new rotating rigid-body dataset with sequences of rotating cubes and rectangular prisms with uniform and non-uniform density.

Joint Estimation of Image Representations and their Lie Invariants

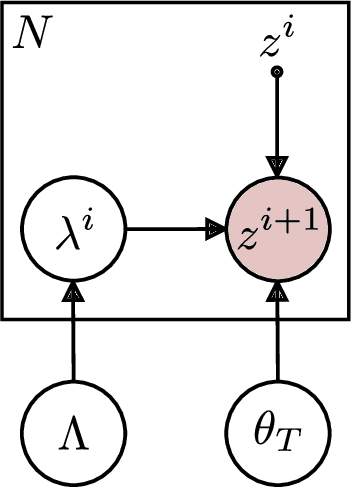
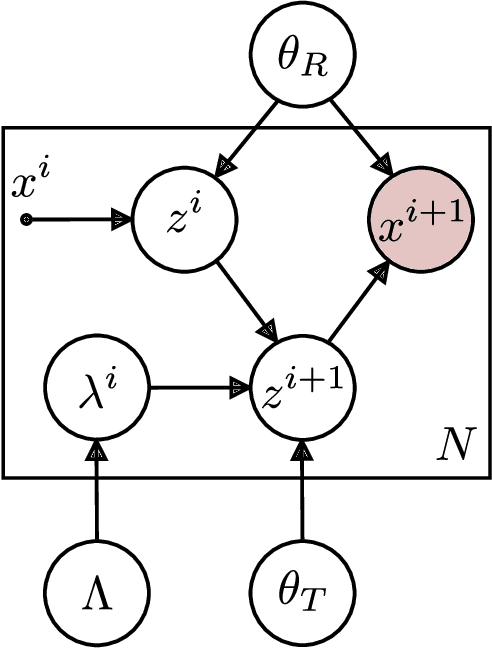
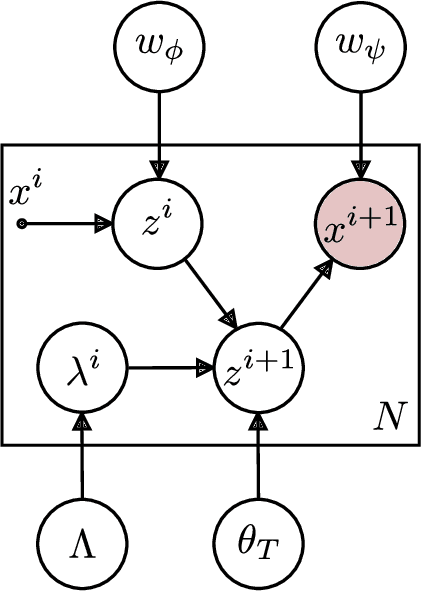
Images encode both the state of the world and its content. The former is useful for tasks such as planning and control, and the latter for classification. The automatic extraction of this information is challenging because of the high-dimensionality and entangled encoding inherent to the image representation. This article introduces two theoretical approaches aimed at the resolution of these challenges. The approaches allow for the interpolation and extrapolation of images from an image sequence by joint estimation of the image representation and the generators of the sequence dynamics. In the first approach, the image representations are learned using probabilistic PCA \cite{tipping1999probabilistic}. The linear-Gaussian conditional distributions allow for a closed form analytical description of the latent distributions but assumes the underlying image manifold is a linear subspace. In the second approach, the image representations are learned using probabilistic nonlinear PCA which relieves the linear manifold assumption at the cost of requiring a variational approximation of the latent distributions. In both approaches, the underlying dynamics of the image sequence are modelled explicitly to disentangle them from the image representations. The dynamics themselves are modelled with Lie group structure which enforces the desirable properties of smoothness and composability of inter-image transformations.

LagNetViP: A Lagrangian Neural Network for Video Prediction

The dominant paradigms for video prediction rely on opaque transition models where neither the equations of motion nor the underlying physical quantities of the system are easily inferred. The equations of motion, as defined by Newton's second law, describe the time evolution of a physical system state and can therefore be applied toward the determination of future system states. In this paper, we introduce a video prediction model where the equations of motion are explicitly constructed from learned representations of the underlying physical quantities. To achieve this, we simultaneously learn a low-dimensional state representation and system Lagrangian. The kinetic and potential energy terms of the Lagrangian are distinctly modelled and the low-dimensional equations of motion are explicitly constructed using the Euler-Lagrange equations. We demonstrate the efficacy of this approach for video prediction on image sequences rendered in modified OpenAI gym Pendulum-v0 and Acrobot environments.