Relational Reasoning On Graphs Using Opinion Dynamics

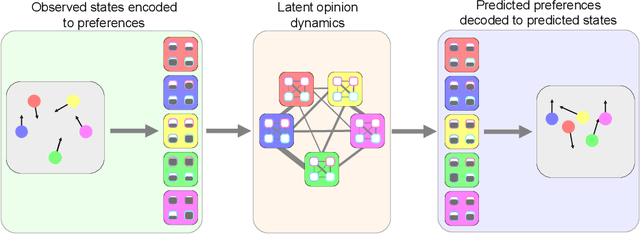
From pedestrians to Kuramoto oscillators, interactions between agents govern how a multitude of dynamical systems evolve in space and time. Discovering how these agents relate to each other can improve our understanding of the often complex dynamics that underlie these systems. Recent works learn to categorize relationships between agents based on observations of their physical behavior. These approaches are limited in that the relationship categories are modelled as independent and mutually exclusive, when in real world systems categories are often interacting. In this work, we introduce a level of abstraction between the physical behavior of agents and the categories that define their behavior. To do this, we learn a mapping from the agents' states to their affinities for each category in a graph neural network. We integrate the physical proximity of agents and their affinities in a nonlinear opinion dynamics model which provides a mechanism to identify mutually exclusive categories, predict an agent's evolution in time, and control an agent's behavior. We demonstrate the utility of our model for learning interpretable categories for mechanical systems, and demonstrate its efficacy on several long-horizon trajectory prediction benchmarks where we consistently out perform existing methods.

Blending Data-Driven Priors in Dynamic Games

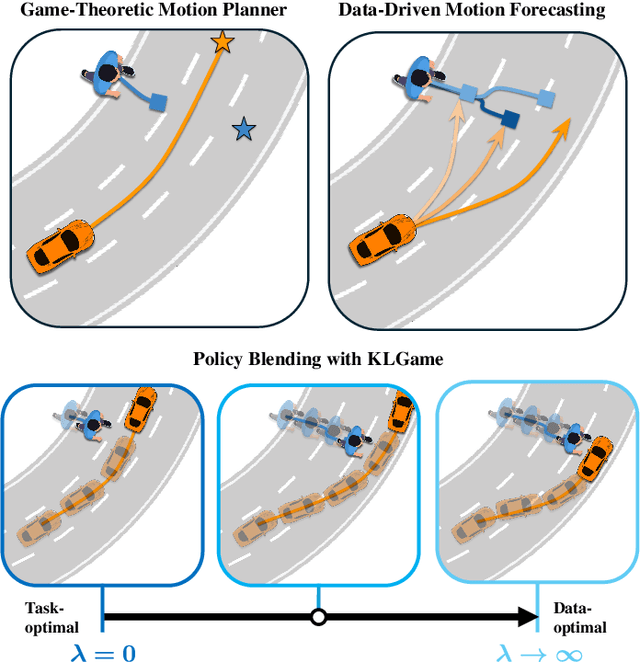
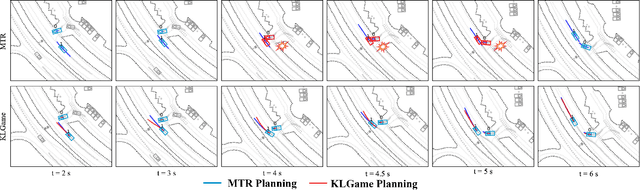
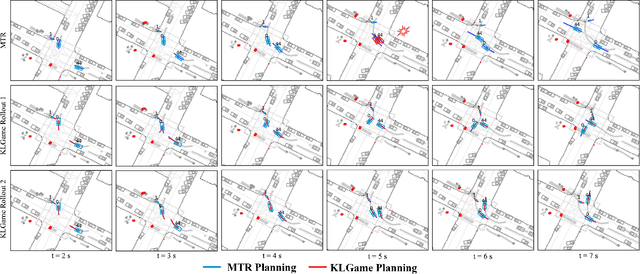
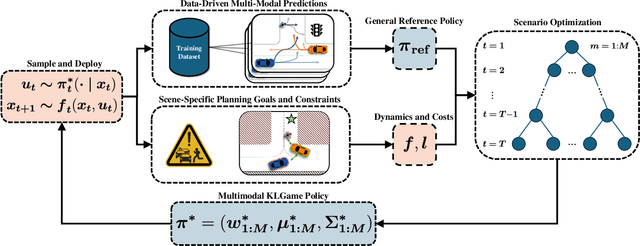
As intelligent robots like autonomous vehicles become increasingly deployed in the presence of people, the extent to which these systems should leverage model-based game-theoretic planners versus data-driven policies for safe, interaction-aware motion planning remains an open question. Existing dynamic game formulations assume all agents are task-driven and behave optimally. However, in reality, humans tend to deviate from the decisions prescribed by these models, and their behavior is better approximated under a noisy-rational paradigm. In this work, we investigate a principled methodology to blend a data-driven reference policy with an optimization-based game-theoretic policy. We formulate KLGame, a type of non-cooperative dynamic game with Kullback-Leibler (KL) regularization with respect to a general, stochastic, and possibly multi-modal reference policy. Our method incorporates, for each decision maker, a tunable parameter that permits modulation between task-driven and data-driven behaviors. We propose an efficient algorithm for computing multimodal approximate feedback Nash equilibrium strategies of KLGame in real time. Through a series of simulated and real-world autonomous driving scenarios, we demonstrate that KLGame policies can more effectively incorporate guidance from the reference policy and account for noisily-rational human behaviors versus non-regularized baselines.

GAME-UP: Game-Aware Mode Enumeration and Understanding for Trajectory Prediction

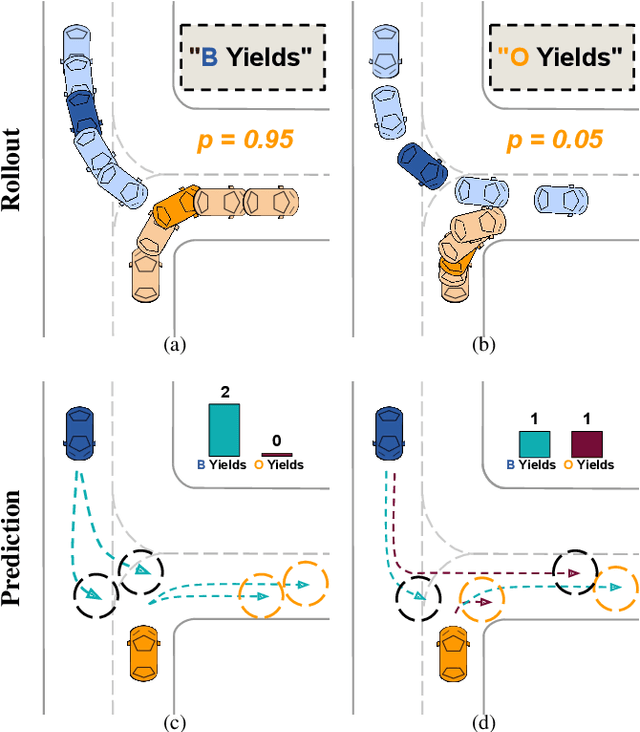
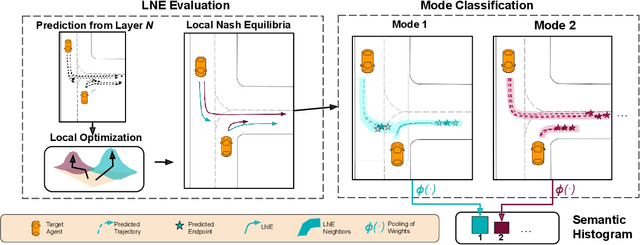
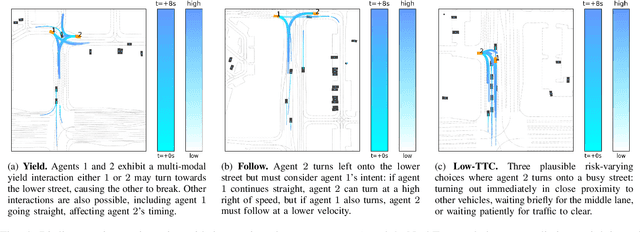
Interactions between road agents present a significant challenge in trajectory prediction, especially in cases involving multiple agents. Because existing diversity-aware predictors do not account for the interactive nature of multi-agent predictions, they may miss these important interaction outcomes. In this paper, we propose GAME-UP, a framework for trajectory prediction that leverages game-theoretic inverse reinforcement learning to improve coverage of multi-modal predictions. We use a training-time game-theoretic numerical analysis as an auxiliary loss resulting in improved coverage and accuracy without presuming a taxonomy of actions for the agents. We demonstrate our approach on the interactive subset of Waymo Open Motion Dataset, including three subsets involving scenarios with high interaction complexity. Experiment results show that our predictor produces accurate predictions while covering twice as many possible interactions versus a baseline model.

Learning Interpretable Dynamics from Images of a Freely Rotating 3D Rigid Body

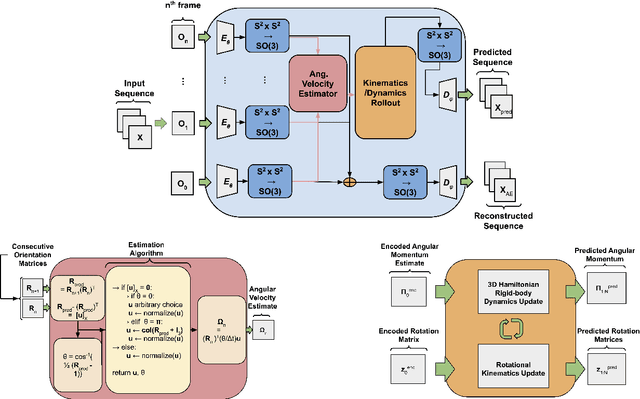
In many real-world settings, image observations of freely rotating 3D rigid bodies, such as satellites, may be available when low-dimensional measurements are not. However, the high-dimensionality of image data precludes the use of classical estimation techniques to learn the dynamics and a lack of interpretability reduces the usefulness of standard deep learning methods. In this work, we present a physics-informed neural network model to estimate and predict 3D rotational dynamics from image sequences. We achieve this using a multi-stage prediction pipeline that maps individual images to a latent representation homeomorphic to $\mathbf{SO}(3)$, computes angular velocities from latent pairs, and predicts future latent states using the Hamiltonian equations of motion with a learned representation of the Hamiltonian. We demonstrate the efficacy of our approach on a new rotating rigid-body dataset with sequences of rotating cubes and rectangular prisms with uniform and non-uniform density.

A Regret Minimization Approach to Multi-Agent Control

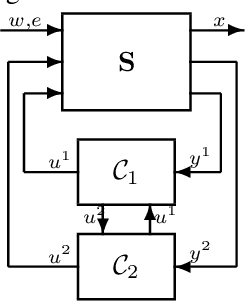
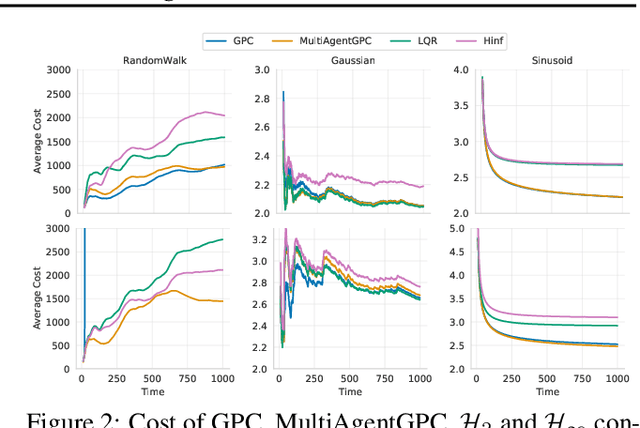
We study the problem of multi-agent control of a dynamical system with known dynamics and adversarial disturbances. Our study focuses on optimal control without centralized precomputed policies, but rather with adaptive control policies for the different agents that are only equipped with a stabilizing controller. We give a reduction from any (standard) regret minimizing control method to a distributed algorithm. The reduction guarantees that the resulting distributed algorithm has low regret relative to the optimal precomputed joint policy. Our methodology involves generalizing online convex optimization to a multi-agent setting and applying recent tools from nonstochastic control derived for a single agent. We empirically evaluate our method on a model of an overactuated aircraft. We show that the distributed method is robust to failure and to adversarial perturbations in the dynamics.

When to Call Your Neighbor? Strategic Communication in Cooperative Stochastic Bandits

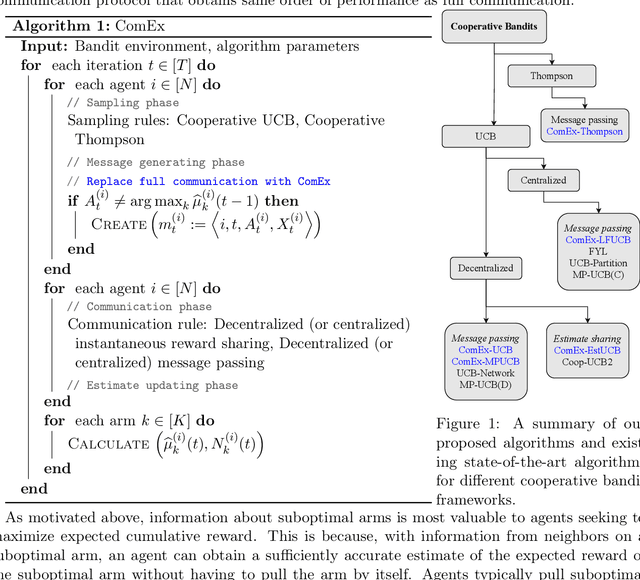
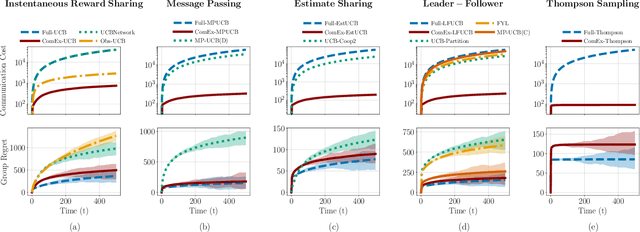
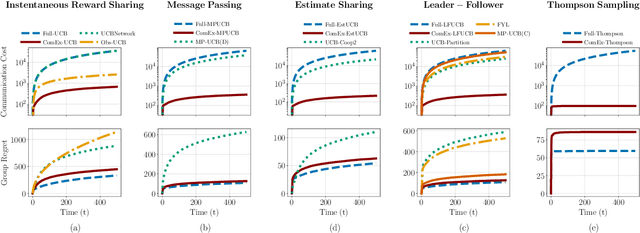
In cooperative bandits, a framework that captures essential features of collective sequential decision making, agents can minimize group regret, and thereby improve performance, by leveraging shared information. However, sharing information can be costly, which motivates developing policies that minimize group regret while also reducing the number of messages communicated by agents. Existing cooperative bandit algorithms obtain optimal performance when agents share information with their neighbors at \textit{every time step}, i.e., full communication. This requires $\Theta(T)$ number of messages, where $T$ is the time horizon of the decision making process. We propose \textit{ComEx}, a novel cost-effective communication protocol in which the group achieves the same order of performance as full communication while communicating only $O(\log T)$ number of messages. Our key step is developing a method to identify and only communicate the information crucial to achieving optimal performance. Further we propose novel algorithms for several benchmark cooperative bandit frameworks and show that our algorithms obtain \textit{state-of-the-art} performance while consistently incurring a significantly smaller communication cost than existing algorithms.

Heterogeneous Explore-Exploit Strategies on Multi-Star Networks

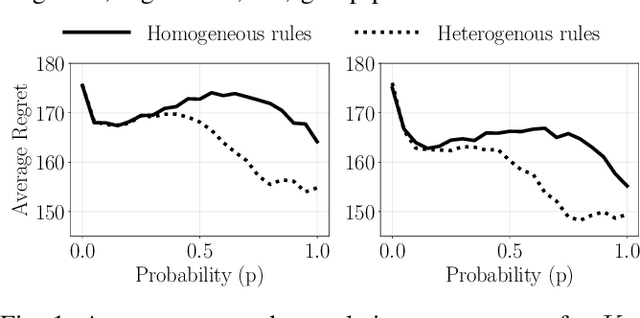
We investigate the benefits of heterogeneity in multi-agent explore-exploit decision making where the goal of the agents is to maximize cumulative group reward. To do so we study a class of distributed stochastic bandit problems in which agents communicate over a multi-star network and make sequential choices among options in the same uncertain environment. Typically, in multi-agent bandit problems, agents use homogeneous decision-making strategies. However, group performance can be improved by incorporating heterogeneity into the choices agents make, especially when the network graph is irregular, i.e. when agents have different numbers of neighbors. We design and analyze new heterogeneous explore-exploit strategies, using the multi-star as the model irregular network graph. The key idea is to enable center agents to do more exploring than they would do using the homogeneous strategy, as a means of providing more useful data to the peripheral agents. In the case all agents broadcast their reward values and choices to their neighbors with the same probability, we provide theoretical guarantees that group performance improves under the proposed heterogeneous strategies as compared to under homogeneous strategies. We use numerical simulations to illustrate our results and to validate our theoretical bounds.