Asher Hancock
Blending Data-Driven Priors in Dynamic Games
Feb 23, 2024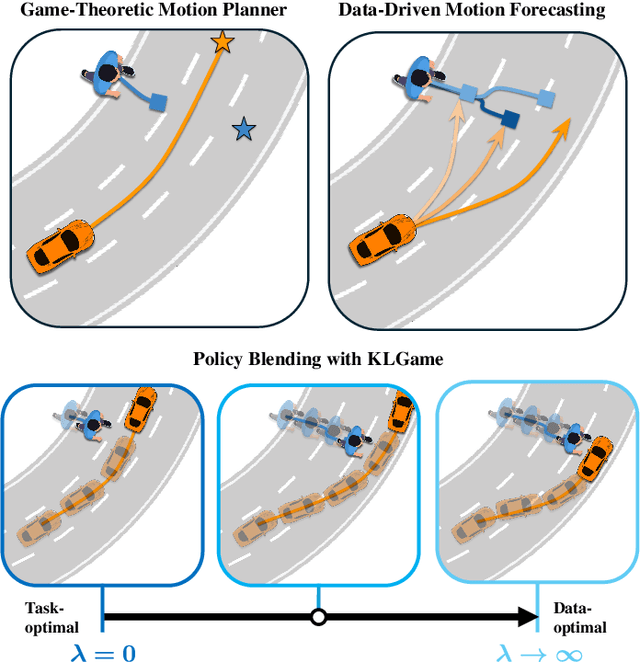
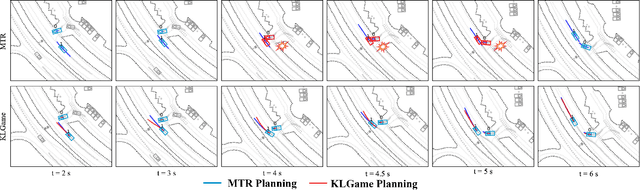
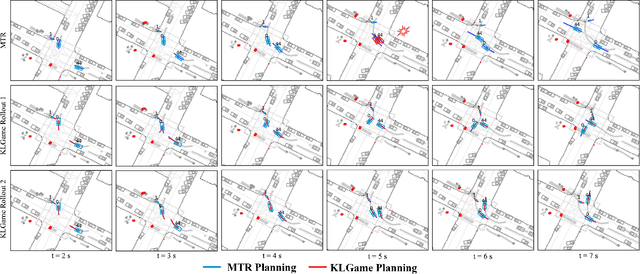
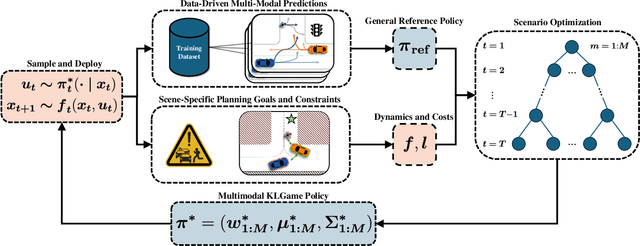
Abstract:As intelligent robots like autonomous vehicles become increasingly deployed in the presence of people, the extent to which these systems should leverage model-based game-theoretic planners versus data-driven policies for safe, interaction-aware motion planning remains an open question. Existing dynamic game formulations assume all agents are task-driven and behave optimally. However, in reality, humans tend to deviate from the decisions prescribed by these models, and their behavior is better approximated under a noisy-rational paradigm. In this work, we investigate a principled methodology to blend a data-driven reference policy with an optimization-based game-theoretic policy. We formulate KLGame, a type of non-cooperative dynamic game with Kullback-Leibler (KL) regularization with respect to a general, stochastic, and possibly multi-modal reference policy. Our method incorporates, for each decision maker, a tunable parameter that permits modulation between task-driven and data-driven behaviors. We propose an efficient algorithm for computing multimodal approximate feedback Nash equilibrium strategies of KLGame in real time. Through a series of simulated and real-world autonomous driving scenarios, we demonstrate that KLGame policies can more effectively incorporate guidance from the reference policy and account for noisily-rational human behaviors versus non-regularized baselines.
PAC-Bayes Generalization Certificates for Learned Inductive Conformal Prediction
Dec 07, 2023Abstract:Inductive Conformal Prediction (ICP) provides a practical and effective approach for equipping deep learning models with uncertainty estimates in the form of set-valued predictions which are guaranteed to contain the ground truth with high probability. Despite the appeal of this coverage guarantee, these sets may not be efficient: the size and contents of the prediction sets are not directly controlled, and instead depend on the underlying model and choice of score function. To remedy this, recent work has proposed learning model and score function parameters using data to directly optimize the efficiency of the ICP prediction sets. While appealing, the generalization theory for such an approach is lacking: direct optimization of empirical efficiency may yield prediction sets that are either no longer efficient on test data, or no longer obtain the required coverage on test data. In this work, we use PAC-Bayes theory to obtain generalization bounds on both the coverage and the efficiency of set-valued predictors which can be directly optimized to maximize efficiency while satisfying a desired test coverage. In contrast to prior work, our framework allows us to utilize the entire calibration dataset to learn the parameters of the model and score function, instead of requiring a separate hold-out set for obtaining test-time coverage guarantees. We leverage these theoretical results to provide a practical algorithm for using calibration data to simultaneously fine-tune the parameters of a model and score function while guaranteeing test-time coverage and efficiency of the resulting prediction sets. We evaluate the approach on regression and classification tasks, and outperform baselines calibrated using a Hoeffding bound-based PAC guarantee on ICP, especially in the low-data regime.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge