SINDy-RL: Interpretable and Efficient Model-Based Reinforcement Learning

Deep reinforcement learning (DRL) has shown significant promise for uncovering sophisticated control policies that interact in environments with complicated dynamics, such as stabilizing the magnetohydrodynamics of a tokamak fusion reactor or minimizing the drag force exerted on an object in a fluid flow. However, these algorithms require an abundance of training examples and may become prohibitively expensive for many applications. In addition, the reliance on deep neural networks often results in an uninterpretable, black-box policy that may be too computationally expensive to use with certain embedded systems. Recent advances in sparse dictionary learning, such as the sparse identification of nonlinear dynamics (SINDy), have shown promise for creating efficient and interpretable data-driven models in the low-data regime. In this work we introduce SINDy-RL, a unifying framework for combining SINDy and DRL to create efficient, interpretable, and trustworthy representations of the dynamics model, reward function, and control policy. We demonstrate the effectiveness of our approaches on benchmark control environments and challenging fluids problems. SINDy-RL achieves comparable performance to state-of-the-art DRL algorithms using significantly fewer interactions in the environment and results in an interpretable control policy orders of magnitude smaller than a deep neural network policy.

A Unified Framework to Enforce, Discover, and Promote Symmetry in Machine Learning

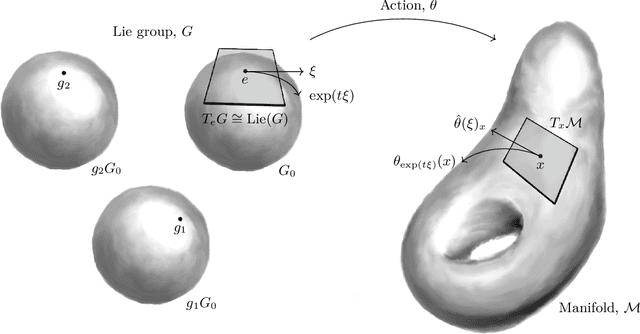
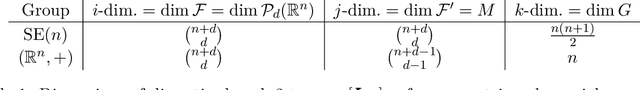
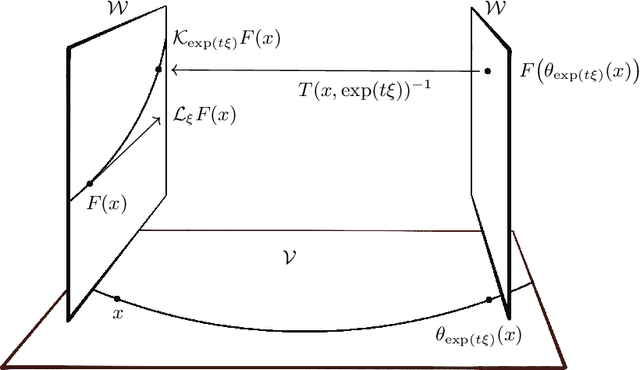
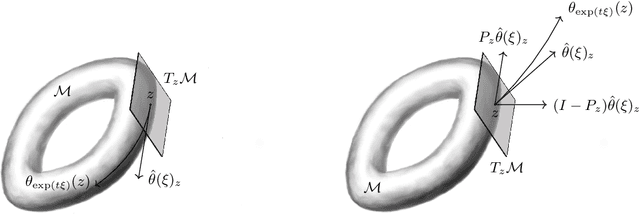
Symmetry is present throughout nature and continues to play an increasingly central role in physics and machine learning. Fundamental symmetries, such as Poincar\'{e} invariance, allow physical laws discovered in laboratories on Earth to be extrapolated to the farthest reaches of the universe. Symmetry is essential to achieving this extrapolatory power in machine learning applications. For example, translation invariance in image classification allows models with fewer parameters, such as convolutional neural networks, to be trained on smaller data sets and achieve state-of-the-art performance. In this paper, we provide a unifying theoretical and methodological framework for incorporating symmetry into machine learning models in three ways: 1. enforcing known symmetry when training a model; 2. discovering unknown symmetries of a given model or data set; and 3. promoting symmetry during training by learning a model that breaks symmetries within a user-specified group of candidates when there is sufficient evidence in the data. We show that these tasks can be cast within a common mathematical framework whose central object is the Lie derivative associated with fiber-linear Lie group actions on vector bundles. We extend and unify several existing results by showing that enforcing and discovering symmetry are linear-algebraic tasks that are dual with respect to the bilinear structure of the Lie derivative. We also propose a novel way to promote symmetry by introducing a class of convex regularization functions based on the Lie derivative and nuclear norm relaxation to penalize symmetry breaking during training of machine learning models. We explain how these ideas can be applied to a wide range of machine learning models including basis function regression, dynamical systems discovery, multilayer perceptrons, and neural networks acting on spatial fields such as images.

Learning to predict 3D rotational dynamics from images of a rigid body with unknown mass distribution

In many real-world settings, image observations of freely rotating 3D rigid bodies, may be available when low-dimensional measurements are not. However, the high-dimensionality of image data precludes the use of classical estimation techniques to learn the dynamics. The usefulness of standard deep learning methods is also limited because an image of a rigid body reveals nothing about the distribution of mass inside the body, which, together with initial angular velocity, is what determines how the body will rotate. We present a physics-informed neural network model to estimate and predict 3D rotational dynamics from image sequences. We achieve this using a multi-stage prediction pipeline that maps individual images to a latent representation homeomorphic to $\mathbf{SO}(3)$, computes angular velocities from latent pairs, and predicts future latent states using the Hamiltonian equations of motion. We demonstrate the efficacy of our approach on new rotating rigid-body datasets of sequences of synthetic images of rotating objects, including cubes, prisms and satellites, with unknown uniform and non-uniform mass distributions.

Learning Interpretable Dynamics from Images of a Freely Rotating 3D Rigid Body

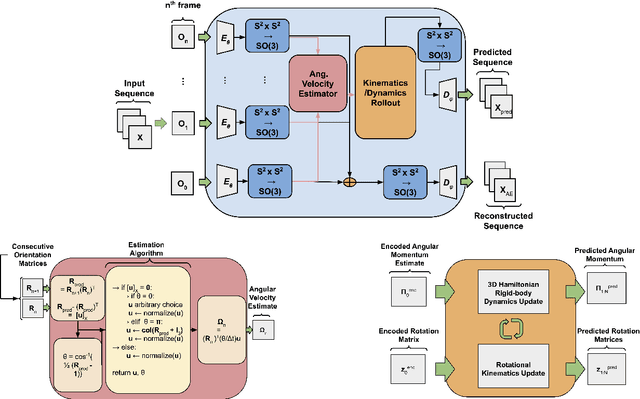
In many real-world settings, image observations of freely rotating 3D rigid bodies, such as satellites, may be available when low-dimensional measurements are not. However, the high-dimensionality of image data precludes the use of classical estimation techniques to learn the dynamics and a lack of interpretability reduces the usefulness of standard deep learning methods. In this work, we present a physics-informed neural network model to estimate and predict 3D rotational dynamics from image sequences. We achieve this using a multi-stage prediction pipeline that maps individual images to a latent representation homeomorphic to $\mathbf{SO}(3)$, computes angular velocities from latent pairs, and predicts future latent states using the Hamiltonian equations of motion with a learned representation of the Hamiltonian. We demonstrate the efficacy of our approach on a new rotating rigid-body dataset with sequences of rotating cubes and rectangular prisms with uniform and non-uniform density.