Heterogeneous Explore-Exploit Strategies on Multi-Star Networks
Paper and Code
Sep 02, 2020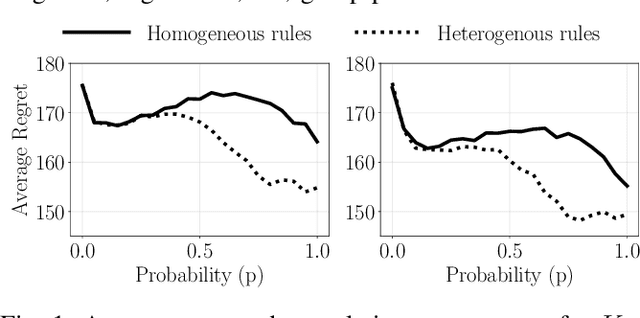

We investigate the benefits of heterogeneity in multi-agent explore-exploit decision making where the goal of the agents is to maximize cumulative group reward. To do so we study a class of distributed stochastic bandit problems in which agents communicate over a multi-star network and make sequential choices among options in the same uncertain environment. Typically, in multi-agent bandit problems, agents use homogeneous decision-making strategies. However, group performance can be improved by incorporating heterogeneity into the choices agents make, especially when the network graph is irregular, i.e. when agents have different numbers of neighbors. We design and analyze new heterogeneous explore-exploit strategies, using the multi-star as the model irregular network graph. The key idea is to enable center agents to do more exploring than they would do using the homogeneous strategy, as a means of providing more useful data to the peripheral agents. In the case all agents broadcast their reward values and choices to their neighbors with the same probability, we provide theoretical guarantees that group performance improves under the proposed heterogeneous strategies as compared to under homogeneous strategies. We use numerical simulations to illustrate our results and to validate our theoretical bounds.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge