When to Call Your Neighbor? Strategic Communication in Cooperative Stochastic Bandits
Paper and Code
Oct 08, 2021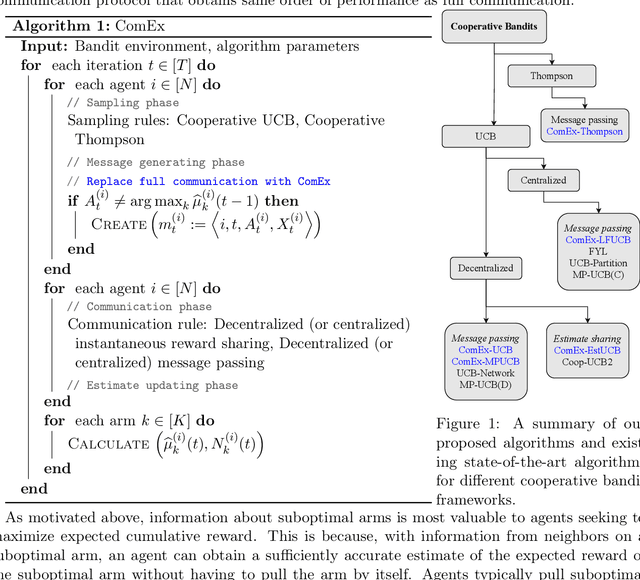
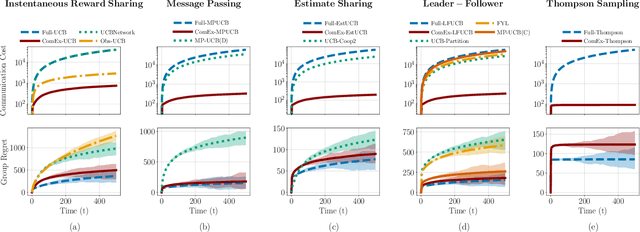
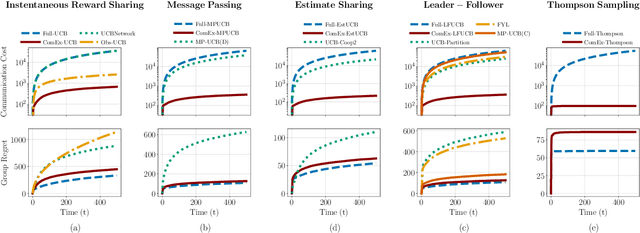
In cooperative bandits, a framework that captures essential features of collective sequential decision making, agents can minimize group regret, and thereby improve performance, by leveraging shared information. However, sharing information can be costly, which motivates developing policies that minimize group regret while also reducing the number of messages communicated by agents. Existing cooperative bandit algorithms obtain optimal performance when agents share information with their neighbors at \textit{every time step}, i.e., full communication. This requires $\Theta(T)$ number of messages, where $T$ is the time horizon of the decision making process. We propose \textit{ComEx}, a novel cost-effective communication protocol in which the group achieves the same order of performance as full communication while communicating only $O(\log T)$ number of messages. Our key step is developing a method to identify and only communicate the information crucial to achieving optimal performance. Further we propose novel algorithms for several benchmark cooperative bandit frameworks and show that our algorithms obtain \textit{state-of-the-art} performance while consistently incurring a significantly smaller communication cost than existing algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge