Surrogate Modeling of 3D Rayleigh-Benard Convection with Equivariant Autoencoders

The use of machine learning for modeling, understanding, and controlling large-scale physics systems is quickly gaining in popularity, with examples ranging from electromagnetism over nuclear fusion reactors and magneto-hydrodynamics to fluid mechanics and climate modeling. These systems -- governed by partial differential equations -- present unique challenges regarding the large number of degrees of freedom and the complex dynamics over many scales both in space and time, and additional measures to improve accuracy and sample efficiency are highly desirable. We present an end-to-end equivariant surrogate model consisting of an equivariant convolutional autoencoder and an equivariant convolutional LSTM using $G$-steerable kernels. As a case study, we consider the three-dimensional Rayleigh-B\'enard convection, which describes the buoyancy-driven fluid flow between a heated bottom and a cooled top plate. While the system is E(2)-equivariant in the horizontal plane, the boundary conditions break the translational equivariance in the vertical direction. Our architecture leverages vertically stacked layers of $D_4$-steerable kernels, with additional partial kernel sharing in the vertical direction for further efficiency improvement. Our results demonstrate significant gains both in sample and parameter efficiency, as well as a better scaling to more complex dynamics, that is, larger Rayleigh numbers. The accompanying code is available under https://github.com/FynnFromme/equivariant-rb-forecasting.

Predicting PDEs Fast and Efficiently with Equivariant Extreme Learning Machines

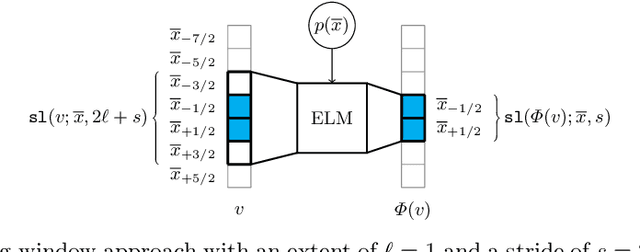
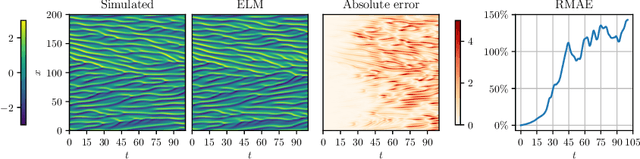
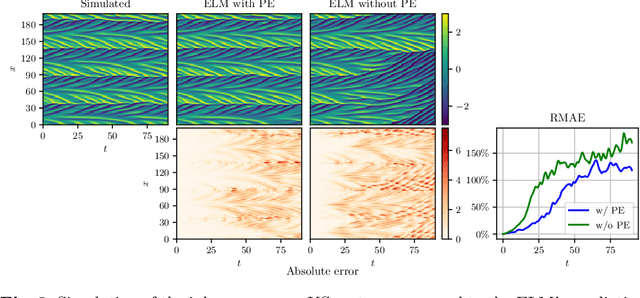
We utilize extreme learning machines for the prediction of partial differential equations (PDEs). Our method splits the state space into multiple windows that are predicted individually using a single model. Despite requiring only few data points (in some cases, our method can learn from a single full-state snapshot), it still achieves high accuracy and can predict the flow of PDEs over long time horizons. Moreover, we show how additional symmetries can be exploited to increase sample efficiency and to enforce equivariance.

On the continuity and smoothness of the value function in reinforcement learning and optimal control

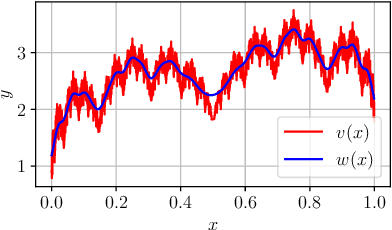
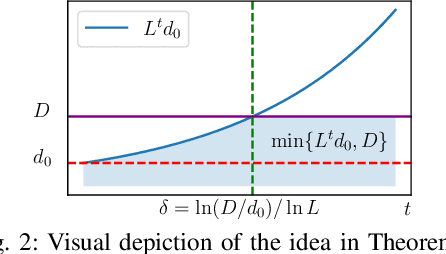
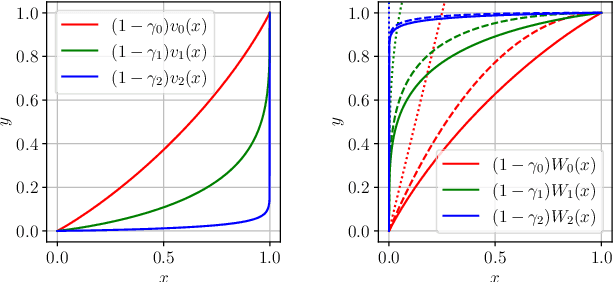
The value function plays a crucial role as a measure for the cumulative future reward an agent receives in both reinforcement learning and optimal control. It is therefore of interest to study how similar the values of neighboring states are, i.e., to investigate the continuity of the value function. We do so by providing and verifying upper bounds on the value function's modulus of continuity. Additionally, we show that the value function is always H\"older continuous under relatively weak assumptions on the underlying system and that non-differentiable value functions can be made differentiable by slightly "disturbing" the system.

Partial observations, coarse graining and equivariance in Koopman operator theory for large-scale dynamical systems

The Koopman operator has become an essential tool for data-driven analysis, prediction and control of complex systems, the main reason being the enormous potential of identifying linear function space representations of nonlinear dynamics from measurements. Until now, the situation where for large-scale systems, we (i) only have access to partial observations (i.e., measurements, as is very common for experimental data) or (ii) deliberately perform coarse graining (for efficiency reasons) has not been treated to its full extent. In this paper, we address the pitfall associated with this situation, that the classical EDMD algorithm does not automatically provide a Koopman operator approximation for the underlying system if we do not carefully select the number of observables. Moreover, we show that symmetries in the system dynamics can be carried over to the Koopman operator, which allows us to massively increase the model efficiency. We also briefly draw a connection to domain decomposition techniques for partial differential equations and present numerical evidence using the Kuramoto--Sivashinsky equation.