Efficient probabilistic surrogate modeling techniques for partially-observed large-scale dynamical systems

This paper is concerned with probabilistic techniques for forecasting dynamical systems described by partial differential equations (such as, for example, the Navier-Stokes equations). In particular, it is investigating and comparing various extensions to the flow matching paradigm that reduce the number of sampling steps. In this regard, it compares direct distillation, progressive distillation, adversarial diffusion distillation, Wasserstein GANs and rectified flows. Moreover, experiments are conducted on a set of challenging systems. In particular, we also address the challenge of directly predicting 2D slices of large-scale 3D simulations, paving the way for efficient inflow generation for solvers.

Bayesian Transfer Operators in Reproducing Kernel Hilbert Spaces

The Koopman operator, as a linear representation of a nonlinear dynamical system, has been attracting attention in many fields of science. Recently, Koopman operator theory has been combined with another concept that is popular in data science: reproducing kernel Hilbert spaces. We follow this thread into Gaussian process methods, and illustrate how these methods can alleviate two pervasive problems with kernel-based Koopman algorithms. The first being sparsity: most kernel methods do not scale well and require an approximation to become practical. We show that not only can the computational demands be reduced, but also demonstrate improved resilience against sensor noise. The second problem involves hyperparameter optimization and dictionary learning to adapt the model to the dynamical system. In summary, the main contribution of this work is the unification of Gaussian process regression and dynamic mode decomposition.

Surrogate Modeling of 3D Rayleigh-Benard Convection with Equivariant Autoencoders

The use of machine learning for modeling, understanding, and controlling large-scale physics systems is quickly gaining in popularity, with examples ranging from electromagnetism over nuclear fusion reactors and magneto-hydrodynamics to fluid mechanics and climate modeling. These systems -- governed by partial differential equations -- present unique challenges regarding the large number of degrees of freedom and the complex dynamics over many scales both in space and time, and additional measures to improve accuracy and sample efficiency are highly desirable. We present an end-to-end equivariant surrogate model consisting of an equivariant convolutional autoencoder and an equivariant convolutional LSTM using $G$-steerable kernels. As a case study, we consider the three-dimensional Rayleigh-B\'enard convection, which describes the buoyancy-driven fluid flow between a heated bottom and a cooled top plate. While the system is E(2)-equivariant in the horizontal plane, the boundary conditions break the translational equivariance in the vertical direction. Our architecture leverages vertically stacked layers of $D_4$-steerable kernels, with additional partial kernel sharing in the vertical direction for further efficiency improvement. Our results demonstrate significant gains both in sample and parameter efficiency, as well as a better scaling to more complex dynamics, that is, larger Rayleigh numbers. The accompanying code is available under https://github.com/FynnFromme/equivariant-rb-forecasting.

Control of Rayleigh-Bénard Convection: Effectiveness of Reinforcement Learning in the Turbulent Regime

Data-driven flow control has significant potential for industry, energy systems, and climate science. In this work, we study the effectiveness of Reinforcement Learning (RL) for reducing convective heat transfer in the 2D Rayleigh-B\'enard Convection (RBC) system under increasing turbulence. We investigate the generalizability of control across varying initial conditions and turbulence levels and introduce a reward shaping technique to accelerate the training. RL agents trained via single-agent Proximal Policy Optimization (PPO) are compared to linear proportional derivative (PD) controllers from classical control theory. The RL agents reduced convection, measured by the Nusselt Number, by up to 33% in moderately turbulent systems and 10% in highly turbulent settings, clearly outperforming PD control in all settings. The agents showed strong generalization performance across different initial conditions and to a significant extent, generalized to higher degrees of turbulence. The reward shaping improved sample efficiency and consistently stabilized the Nusselt Number to higher turbulence levels.

Surrogate-assisted multi-objective design of complex multibody systems

The optimization of large-scale multibody systems is a numerically challenging task, in particular when considering multiple conflicting criteria at the same time. In this situation, we need to approximate the Pareto set of optimal compromises, which is significantly more expensive than finding a single optimum in single-objective optimization. To prevent large costs, the usage of surrogate models, constructed from a small but informative number of expensive model evaluations, is a very popular and widely studied approach. The central challenge then is to ensure a high quality (that is, near-optimality) of the solutions that were obtained using the surrogate model, which can be hard to guarantee with a single pre-computed surrogate. We present a back-and-forth approach between surrogate modeling and multi-objective optimization to improve the quality of the obtained solutions. Using the example of an expensive-to-evaluate multibody system, we compare different strategies regarding multi-objective optimization, sampling and also surrogate modeling, to identify the most promising approach in terms of computational efficiency and solution quality.

The impact of AI on engineering design procedures for dynamical systems

Artificial intelligence (AI) is driving transformative changes across numerous fields, revolutionizing conventional processes and creating new opportunities for innovation. The development of mechatronic systems is undergoing a similar transformation. Over the past decade, modeling, simulation, and optimization techniques have become integral to the design process, paving the way for the adoption of AI-based methods. In this paper, we examine the potential for integrating AI into the engineering design process, using the V-model from the VDI guideline 2206, considered the state-of-the-art in product design, as a foundation. We identify and classify AI methods based on their suitability for specific stages within the engineering product design workflow. Furthermore, we present a series of application examples where AI-assisted design has been successfully implemented by the authors. These examples, drawn from research projects within the DFG Priority Program \emph{SPP~2353: Daring More Intelligence - Design Assistants in Mechanics and Dynamics}, showcase a diverse range of applications across mechanics and mechatronics, including areas such as acoustics and robotics.

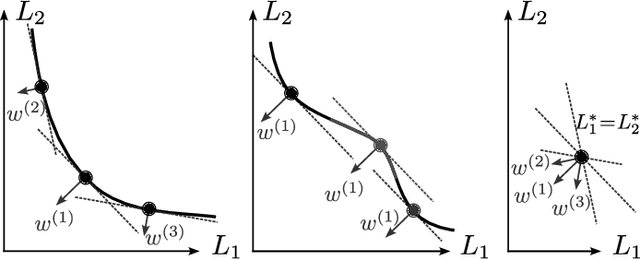
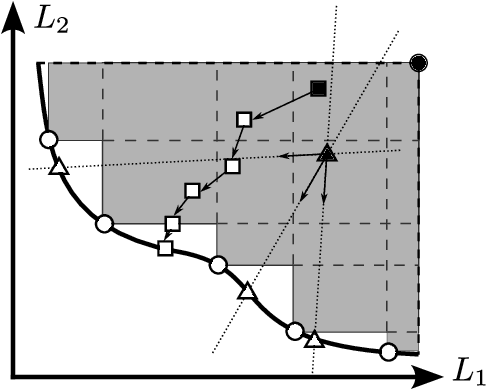
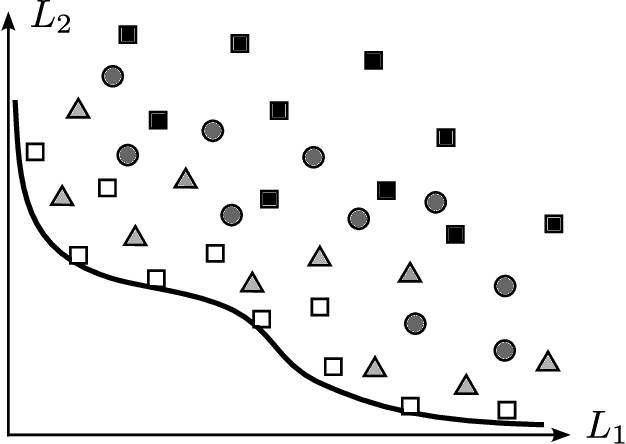
Multi-objective Deep Learning: Taxonomy and Survey of the State of the Art

Simultaneously considering multiple objectives in machine learning has been a popular approach for several decades, with various benefits for multi-task learning, the consideration of secondary goals such as sparsity, or multicriteria hyperparameter tuning. However - as multi-objective optimization is significantly more costly than single-objective optimization - the recent focus on deep learning architectures poses considerable additional challenges due to the very large number of parameters, strong nonlinearities and stochasticity. This survey covers recent advancements in the area of multi-objective deep learning. We introduce a taxonomy of existing methods - based on the type of training algorithm as well as the decision maker's needs - before listing recent advancements, and also successful applications. All three main learning paradigms supervised learning, unsupervised learning and reinforcement learning are covered, and we also address the recently very popular area of generative modeling.

MOREL: Enhancing Adversarial Robustness through Multi-Objective Representation Learning

Extensive research has shown that deep neural networks (DNNs) are vulnerable to slight adversarial perturbations$-$small changes to the input data that appear insignificant but cause the model to produce drastically different outputs. In addition to augmenting training data with adversarial examples generated from a specific attack method, most of the current defense strategies necessitate modifying the original model architecture components to improve robustness or performing test-time data purification to handle adversarial attacks. In this work, we demonstrate that strong feature representation learning during training can significantly enhance the original model's robustness. We propose MOREL, a multi-objective feature representation learning approach, encouraging classification models to produce similar features for inputs within the same class, despite perturbations. Our training method involves an embedding space where cosine similarity loss and multi-positive contrastive loss are used to align natural and adversarial features from the model encoder and ensure tight clustering. Concurrently, the classifier is motivated to achieve accurate predictions. Through extensive experiments, we demonstrate that our approach significantly enhances the robustness of DNNs against white-box and black-box adversarial attacks, outperforming other methods that similarly require no architectural changes or test-time data purification. Our code is available at https://github.com/salomonhotegni/MOREL

Common pitfalls to avoid while using multiobjective optimization in machine learning

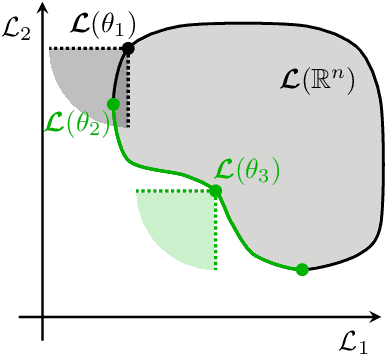
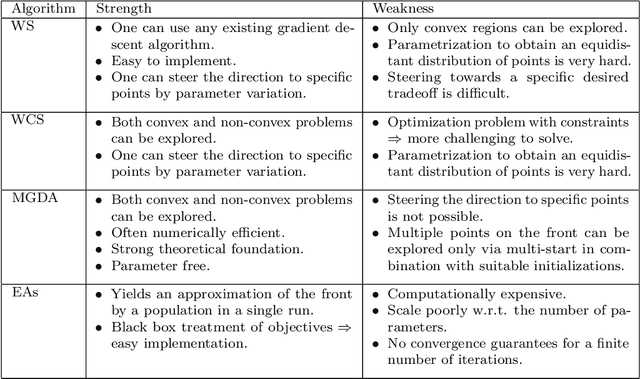
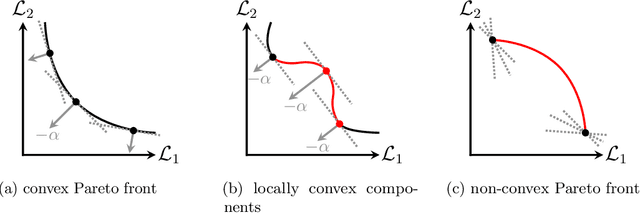
Recently, there has been an increasing interest in exploring the application of multiobjective optimization (MOO) in machine learning (ML). The interest is driven by the numerous situations in real-life applications where multiple objectives need to be optimized simultaneously. A key aspect of MOO is the existence of a Pareto set, rather than a single optimal solution, which illustrates the inherent trade-offs between objectives. Despite its potential, there is a noticeable lack of satisfactory literature that could serve as an entry-level guide for ML practitioners who want to use MOO. Hence, our goal in this paper is to produce such a resource. We critically review previous studies, particularly those involving MOO in deep learning (using Physics-Informed Neural Networks (PINNs) as a guiding example), and identify misconceptions that highlight the need for a better grasp of MOO principles in ML. Using MOO of PINNs as a case study, we demonstrate the interplay between the data loss and the physics loss terms. We highlight the most common pitfalls one should avoid while using MOO techniques in ML. We begin by establishing the groundwork for MOO, focusing on well-known approaches such as the weighted sum (WS) method, alongside more complex techniques like the multiobjective gradient descent algorithm (MGDA). Additionally, we compare the results obtained from the WS and MGDA with one of the most common evolutionary algorithms, NSGA-II. We emphasize the importance of understanding the specific problem, the objective space, and the selected MOO method, while also noting that neglecting factors such as convergence can result in inaccurate outcomes and, consequently, a non-optimal solution. Our goal is to offer a clear and practical guide for ML practitioners to effectively apply MOO, particularly in the context of DL.

Predicting PDEs Fast and Efficiently with Equivariant Extreme Learning Machines

We utilize extreme learning machines for the prediction of partial differential equations (PDEs). Our method splits the state space into multiple windows that are predicted individually using a single model. Despite requiring only few data points (in some cases, our method can learn from a single full-state snapshot), it still achieves high accuracy and can predict the flow of PDEs over long time horizons. Moreover, we show how additional symmetries can be exploited to increase sample efficiency and to enforce equivariance.