Koopman-Based Surrogate Modelling of Turbulent Rayleigh-Bénard Convection

Several related works have introduced Koopman-based Machine Learning architectures as a surrogate model for dynamical systems. These architectures aim to learn non-linear measurements (also known as observables) of the system's state that evolve by a linear operator and are, therefore, amenable to model-based linear control techniques. So far, mainly simple systems have been targeted, and Koopman architectures as reduced-order models for more complex dynamics have not been fully explored. Hence, we use a Koopman-inspired architecture called the Linear Recurrent Autoencoder Network (LRAN) for learning reduced-order dynamics in convection flows of a Rayleigh B\'enard Convection (RBC) system at different amounts of turbulence. The data is obtained from direct numerical simulations of the RBC system. A traditional fluid dynamics method, the Kernel Dynamic Mode Decomposition (KDMD), is used to compare the LRAN. For both methods, we performed hyperparameter sweeps to identify optimal settings. We used a Normalized Sum of Square Error measure for the quantitative evaluation of the models, and we also studied the model predictions qualitatively. We obtained more accurate predictions with the LRAN than with KDMD in the most turbulent setting. We conjecture that this is due to the LRAN's flexibility in learning complicated observables from data, thereby serving as a viable surrogate model for the main structure of fluid dynamics in turbulent convection settings. In contrast, KDMD was more effective in lower turbulence settings due to the repetitiveness of the convection flow. The feasibility of Koopman-based surrogate models for turbulent fluid flows opens possibilities for efficient model-based control techniques useful in a variety of industrial settings.

An Industry 4.0 example: real-time quality control for steel-based mass production using Machine Learning on non-invasive sensor data

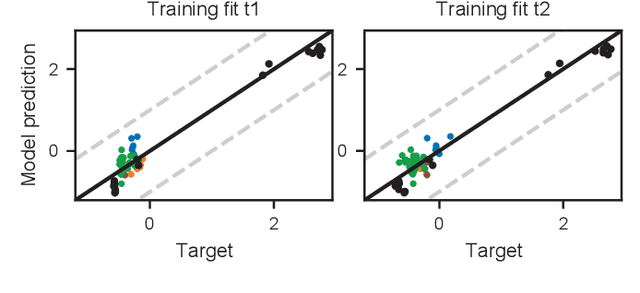
Insufficient steel quality in mass production can cause extremely costly damage to tooling, production downtimes and low quality products. Automatic, fast and cheap strategies to estimate essential material properties for quality control, risk mitigation and the prediction of faults are highly desirable. In this work we analyse a high throughput production line of steel-based products. Currently, the material quality is checked using manual destructive testing, which is slow, wasteful and covers only a tiny fraction of the material. To achieve complete testing coverage our industrial collaborator developed a contactless, non-invasive, electromagnetic sensor to measure all material during production in real-time. Our contribution is three-fold: 1) We show in a controlled experiment that the sensor can distinguish steel with deliberately altered properties. 2) 48 steel coils were fully measured non-invasively and additional destructive tests were conducted on samples to serve as ground truth. A linear model is fitted to predict from the non-invasive measurements two key material properties (yield strength and tensile strength) that normally are obtained by destructive tests. The performance is evaluated in leave-one-coil-out cross-validation. 3) The resulting model is used to analyse the material properties and the relationship with logged product faults on real production data of ~108 km of processed material measured with the non-invasive sensor. The model achieves an excellent performance (F3-score of 0.95) predicting material running out of specifications for the tensile strength. The combination of model predictions and logged product faults shows that if a significant percentage of estimated yield stress values is out of specification, the risk of product faults is high. Our analysis demonstrates promising directions for real-time quality control, risk monitoring and fault detection.

Complex-valued embeddings of generic proximity data

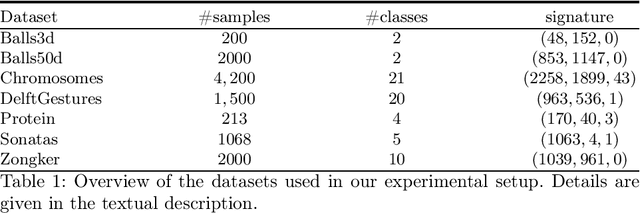
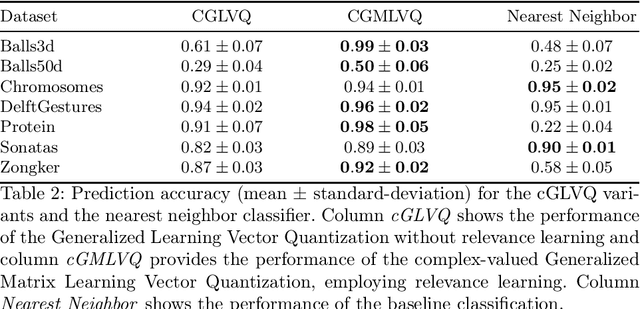
Proximities are at the heart of almost all machine learning methods. If the input data are given as numerical vectors of equal lengths, euclidean distance, or a Hilbertian inner product is frequently used in modeling algorithms. In a more generic view, objects are compared by a (symmetric) similarity or dissimilarity measure, which may not obey particular mathematical properties. This renders many machine learning methods invalid, leading to convergence problems and the loss of guarantees, like generalization bounds. In many cases, the preferred dissimilarity measure is not metric, like the earth mover distance, or the similarity measure may not be a simple inner product in a Hilbert space but in its generalization a Krein space. If the input data are non-vectorial, like text sequences, proximity-based learning is used or ngram embedding techniques can be applied. Standard embeddings lead to the desired fixed-length vector encoding, but are costly and have substantial limitations in preserving the original data's full information. As an information preserving alternative, we propose a complex-valued vector embedding of proximity data. This allows suitable machine learning algorithms to use these fixed-length, complex-valued vectors for further processing. The complex-valued data can serve as an input to complex-valued machine learning algorithms. In particular, we address supervised learning and use extensions of prototype-based learning. The proposed approach is evaluated on a variety of standard benchmarks and shows strong performance compared to traditional techniques in processing non-metric or non-psd proximity data.

Supervised Learning in the Presence of Concept Drift: A modelling framework

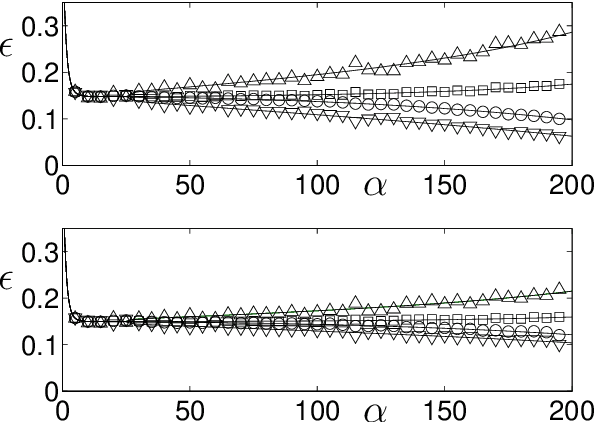
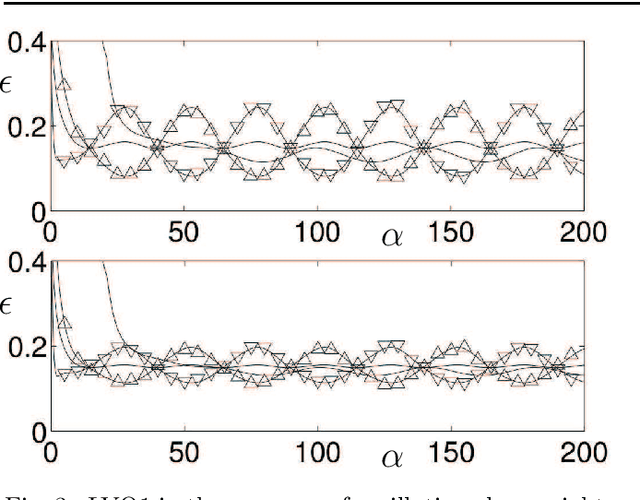
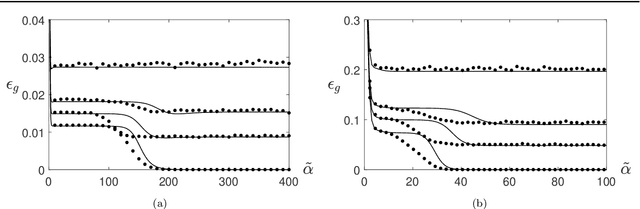
We present a modelling framework for the investigation of supervised learning in non-stationary environments. Specifically, we model two example types of learning systems: prototype-based Learning Vector Quantization (LVQ) for classification and shallow, layered neural networks for regression tasks. We investigate so-called student teacher scenarios in which the systems are trained from a stream of high-dimensional, labeled data. Properties of the target task are considered to be non-stationary due to drift processes while the training is performed. Different types of concept drift are studied, which affect the density of example inputs only, the target rule itself, or both. By applying methods from statistical physics, we develop a modelling framework for the mathematical analysis of the training dynamics in non-stationary environments. Our results show that standard LVQ algorithms are already suitable for the training in non-stationary environments to a certain extent. However, the application of weight decay as an explicit mechanism of forgetting does not improve the performance under the considered drift processes. Furthermore, we investigate gradient-based training of layered neural networks with sigmoidal activation functions and compare with the use of rectified linear units (ReLU). Our findings show that the sensitivity to concept drift and the effectiveness of weight decay differs significantly between the two types of activation function.

Hidden Unit Specialization in Layered Neural Networks: ReLU vs. Sigmoidal Activation

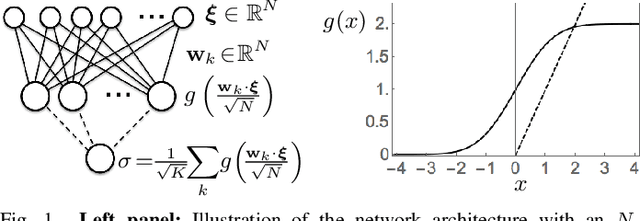
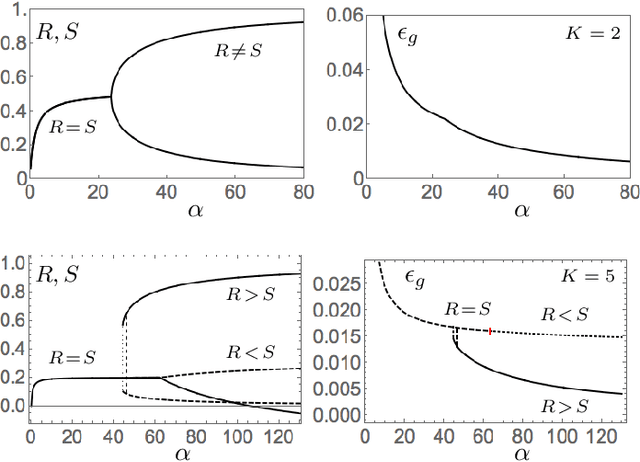
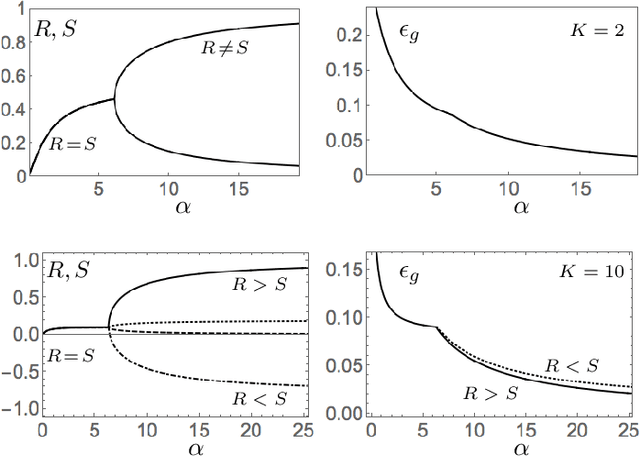
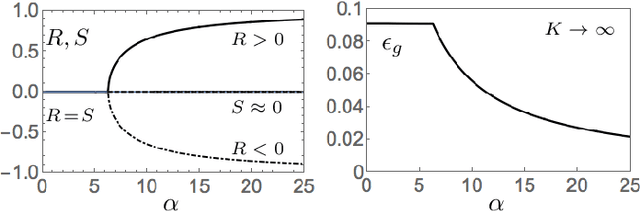
We study layered neural networks of rectified linear units (ReLU) in a modelling framework for stochastic training processes. The comparison with sigmoidal activation functions is in the center of interest. We compute typical learning curves for shallow networks with K hidden units in matching student teacher scenarios. The systems exhibit sudden changes of the generalization performance via the process of hidden unit specialization at critical sizes of the training set. Surprisingly, our results show that the training behavior of ReLU networks is qualitatively different from that of networks with sigmoidal activations. In networks with K >= 3 sigmoidal hidden units, the transition is discontinuous: Specialized network configurations co-exist and compete with states of poor performance even for very large training sets. On the contrary, the use of ReLU activations results in continuous transitions for all K: For large enough training sets, two competing, differently specialized states display similar generalization abilities, which coincide exactly for large networks in the limit K to infinity.

Segmentation of blood vessels in retinal fundus images

In recent years, several automatic segmentation methods have been proposed for blood vessels in retinal fundus images, ranging from using cheap and fast trainable filters to complicated neural networks and even deep learning. One example of a filted-based segmentation method is B-COSFIRE. In this approach the image filter is trained with example prototype patterns, to which the filter becomes selective by finding points in a Difference of Gaussian response on circles around the center with large intensity variation. In this paper we discuss and evaluate several of these vessel segmentation methods. We take a closer look at B-COSFIRE and study the performance of B-COSFIRE on the recently published IOSTAR dataset by experiments and we examine how the parameter values affect the performance. In the experiment we manage to reach a segmentation accuracy of 0.9419. Based on our findings we discuss when B-COSFIRE is the preferred method to use and in which circumstances it could be beneficial to use a more (computationally) complex segmentation method. We also shortly discuss areas beyond blood vessel segmentation where these methods can be used to segment elongated structures, such as rivers in satellite images or nerves of a leaf.

On-line learning dynamics of ReLU neural networks using statistical physics techniques

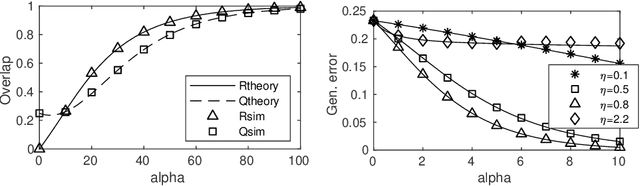
We introduce exact macroscopic on-line learning dynamics of two-layer neural networks with ReLU units in the form of a system of differential equations, using techniques borrowed from statistical physics. For the first experiments, numerical solutions reveal similar behavior compared to sigmoidal activation researched in earlier work. In these experiments the theoretical results show good correspondence with simulations. In ove-rrealizable and unrealizable learning scenarios, the learning behavior of ReLU networks shows distinctive characteristics compared to sigmoidal networks.