Aligning Generalisation Between Humans and Machines

Recent advances in AI -- including generative approaches -- have resulted in technology that can support humans in scientific discovery and decision support but may also disrupt democracies and target individuals. The responsible use of AI increasingly shows the need for human-AI teaming, necessitating effective interaction between humans and machines. A crucial yet often overlooked aspect of these interactions is the different ways in which humans and machines generalise. In cognitive science, human generalisation commonly involves abstraction and concept learning. In contrast, AI generalisation encompasses out-of-domain generalisation in machine learning, rule-based reasoning in symbolic AI, and abstraction in neuro-symbolic AI. In this perspective paper, we combine insights from AI and cognitive science to identify key commonalities and differences across three dimensions: notions of generalisation, methods for generalisation, and evaluation of generalisation. We map the different conceptualisations of generalisation in AI and cognitive science along these three dimensions and consider their role in human-AI teaming. This results in interdisciplinary challenges across AI and cognitive science that must be tackled to provide a foundation for effective and cognitively supported alignment in human-AI teaming scenarios.

Iterated Relevance Matrix Analysis (IRMA) for the identification of class-discriminative subspaces

We introduce and investigate the iterated application of Generalized Matrix Learning Vector Quantizaton for the analysis of feature relevances in classification problems, as well as for the construction of class-discriminative subspaces. The suggested Iterated Relevance Matrix Analysis (IRMA) identifies a linear subspace representing the classification specific information of the considered data sets using Generalized Matrix Learning Vector Quantization (GMLVQ). By iteratively determining a new discriminative subspace while projecting out all previously identified ones, a combined subspace carrying all class-specific information can be found. This facilitates a detailed analysis of feature relevances, and enables improved low-dimensional representations and visualizations of labeled data sets. Additionally, the IRMA-based class-discriminative subspace can be used for dimensionality reduction and the training of robust classifiers with potentially improved performance.

Interpretable Models Capable of Handling Systematic Missingness in Imbalanced Classes and Heterogeneous Datasets

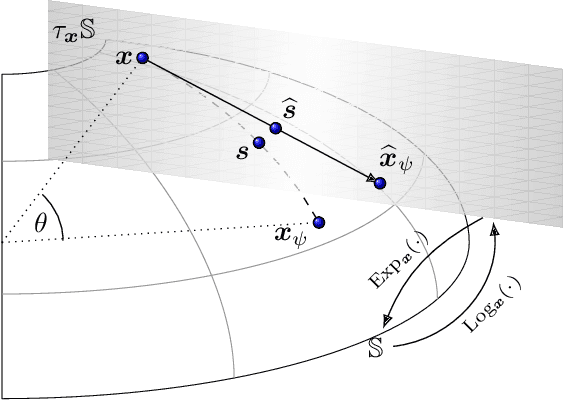
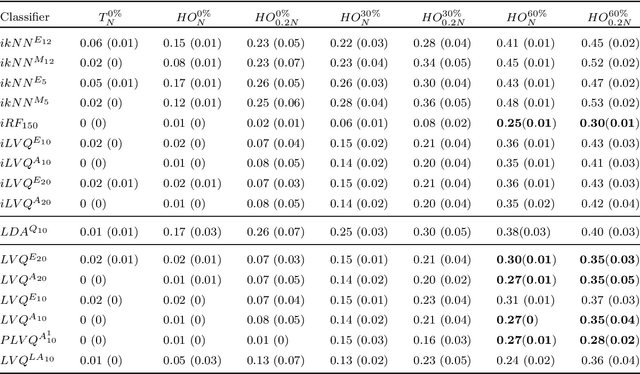
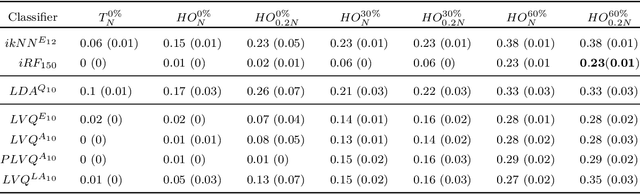
Application of interpretable machine learning techniques on medical datasets facilitate early and fast diagnoses, along with getting deeper insight into the data. Furthermore, the transparency of these models increase trust among application domain experts. Medical datasets face common issues such as heterogeneous measurements, imbalanced classes with limited sample size, and missing data, which hinder the straightforward application of machine learning techniques. In this paper we present a family of prototype-based (PB) interpretable models which are capable of handling these issues. The models introduced in this contribution show comparable or superior performance to alternative techniques applicable in such situations. However, unlike ensemble based models, which have to compromise on easy interpretation, the PB models here do not. Moreover we propose a strategy of harnessing the power of ensembles while maintaining the intrinsic interpretability of the PB models, by averaging the model parameter manifolds. All the models were evaluated on a synthetic (publicly available dataset) in addition to detailed analyses of two real-world medical datasets (one publicly available). Results indicated that the models and strategies we introduced addressed the challenges of real-world medical data, while remaining computationally inexpensive and transparent, as well as similar or superior in performance compared to their alternatives.

Complex-valued embeddings of generic proximity data

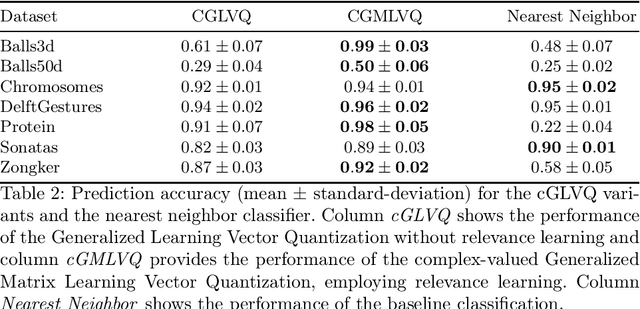
Proximities are at the heart of almost all machine learning methods. If the input data are given as numerical vectors of equal lengths, euclidean distance, or a Hilbertian inner product is frequently used in modeling algorithms. In a more generic view, objects are compared by a (symmetric) similarity or dissimilarity measure, which may not obey particular mathematical properties. This renders many machine learning methods invalid, leading to convergence problems and the loss of guarantees, like generalization bounds. In many cases, the preferred dissimilarity measure is not metric, like the earth mover distance, or the similarity measure may not be a simple inner product in a Hilbert space but in its generalization a Krein space. If the input data are non-vectorial, like text sequences, proximity-based learning is used or ngram embedding techniques can be applied. Standard embeddings lead to the desired fixed-length vector encoding, but are costly and have substantial limitations in preserving the original data's full information. As an information preserving alternative, we propose a complex-valued vector embedding of proximity data. This allows suitable machine learning algorithms to use these fixed-length, complex-valued vectors for further processing. The complex-valued data can serve as an input to complex-valued machine learning algorithms. In particular, we address supervised learning and use extensions of prototype-based learning. The proposed approach is evaluated on a variety of standard benchmarks and shows strong performance compared to traditional techniques in processing non-metric or non-psd proximity data.

Supervised Learning in the Presence of Concept Drift: A modelling framework

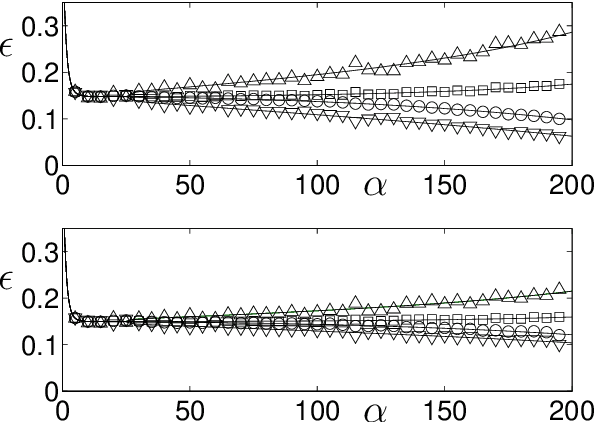
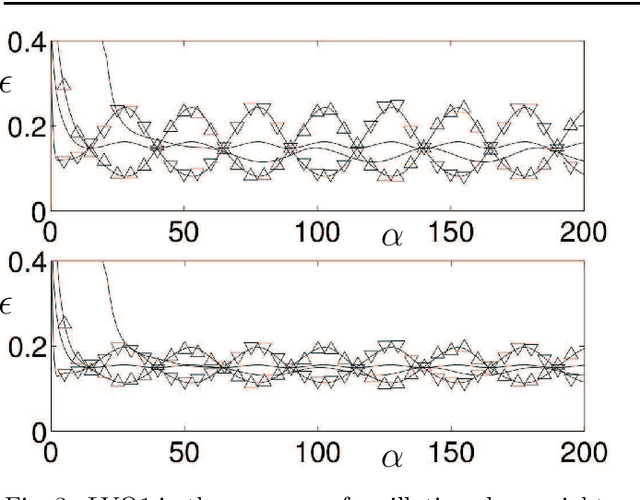
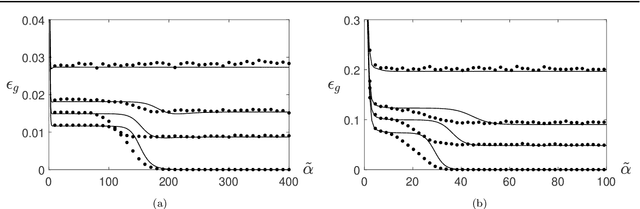
We present a modelling framework for the investigation of supervised learning in non-stationary environments. Specifically, we model two example types of learning systems: prototype-based Learning Vector Quantization (LVQ) for classification and shallow, layered neural networks for regression tasks. We investigate so-called student teacher scenarios in which the systems are trained from a stream of high-dimensional, labeled data. Properties of the target task are considered to be non-stationary due to drift processes while the training is performed. Different types of concept drift are studied, which affect the density of example inputs only, the target rule itself, or both. By applying methods from statistical physics, we develop a modelling framework for the mathematical analysis of the training dynamics in non-stationary environments. Our results show that standard LVQ algorithms are already suitable for the training in non-stationary environments to a certain extent. However, the application of weight decay as an explicit mechanism of forgetting does not improve the performance under the considered drift processes. Furthermore, we investigate gradient-based training of layered neural networks with sigmoidal activation functions and compare with the use of rectified linear units (ReLU). Our findings show that the sensitivity to concept drift and the effectiveness of weight decay differs significantly between the two types of activation function.

Feature Relevance Determination for Ordinal Regression in the Context of Feature Redundancies and Privileged Information

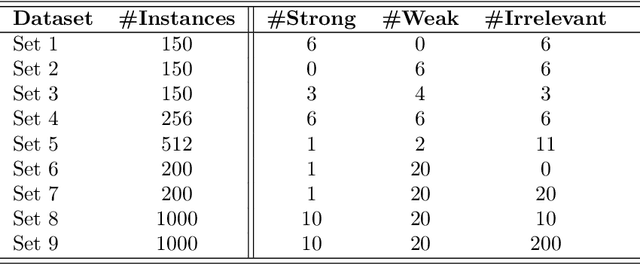
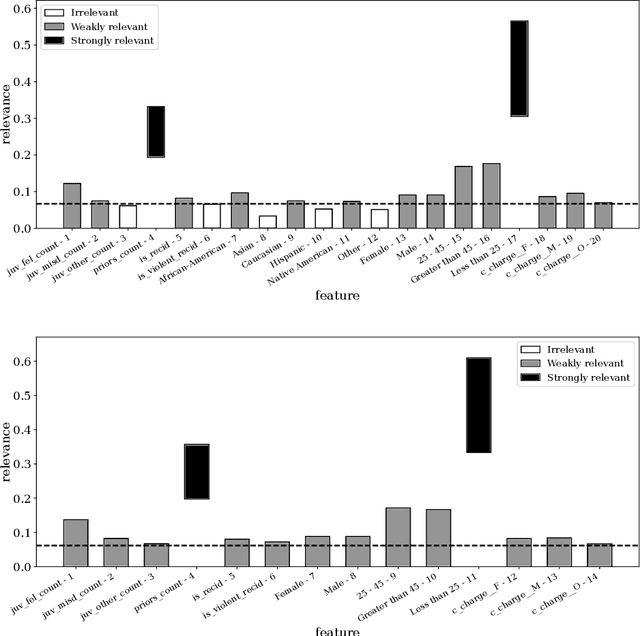
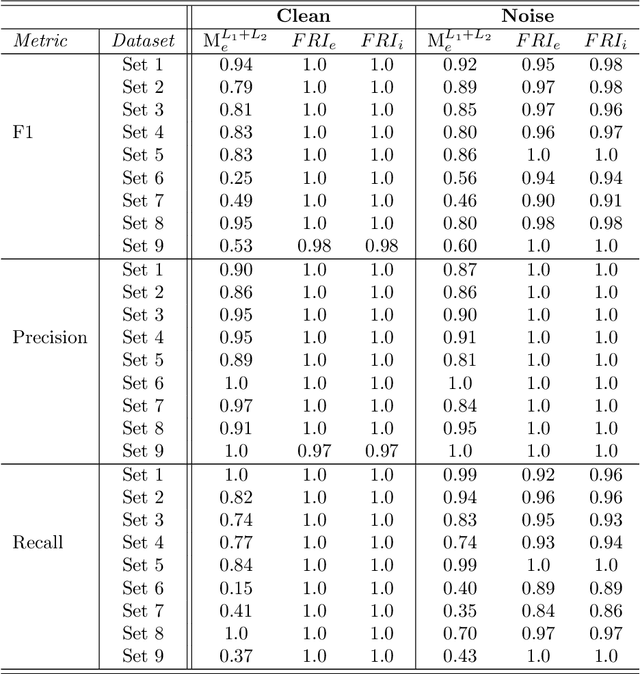
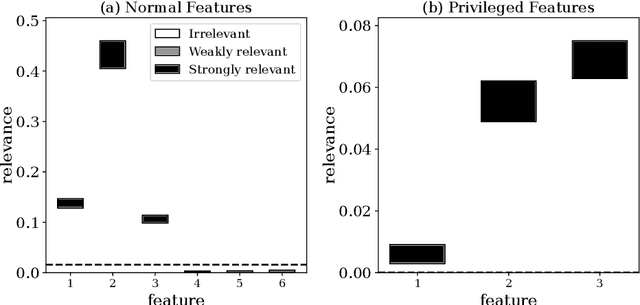
Advances in machine learning technologies have led to increasingly powerful models in particular in the context of big data. Yet, many application scenarios demand for robustly interpretable models rather than optimum model accuracy; as an example, this is the case if potential biomarkers or causal factors should be discovered based on a set of given measurements. In this contribution, we focus on feature selection paradigms, which enable us to uncover relevant factors of a given regularity based on a sparse model. We focus on the important specific setting of linear ordinal regression, i.e.\ data have to be ranked into one of a finite number of ordered categories by a linear projection. Unlike previous work, we consider the case that features are potentially redundant, such that no unique minimum set of relevant features exists. We aim for an identification of all strongly and all weakly relevant features as well as their type of relevance (strong or weak); we achieve this goal by determining feature relevance bounds, which correspond to the minimum and maximum feature relevance, respectively, if searched over all equivalent models. In addition, we discuss how this setting enables us to substitute some of the features, e.g.\ due to their semantics, and how to extend the framework of feature relevance intervals to the setting of privileged information, i.e.\ potentially relevant information is available for training purposes only, but cannot be used for the prediction itself.

Hidden Unit Specialization in Layered Neural Networks: ReLU vs. Sigmoidal Activation

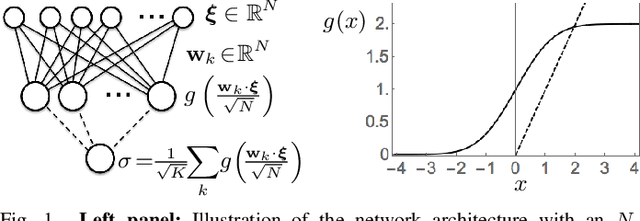
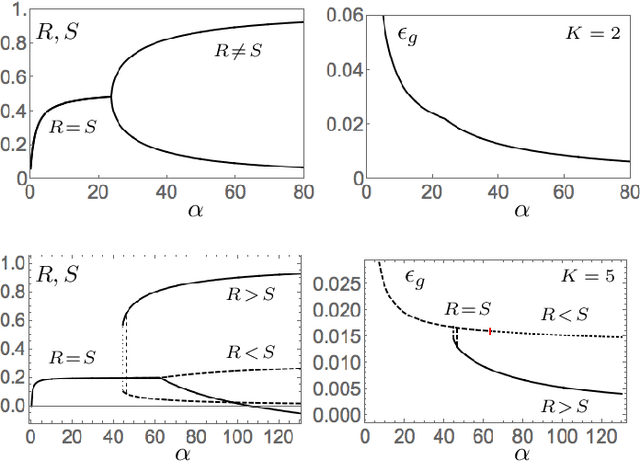
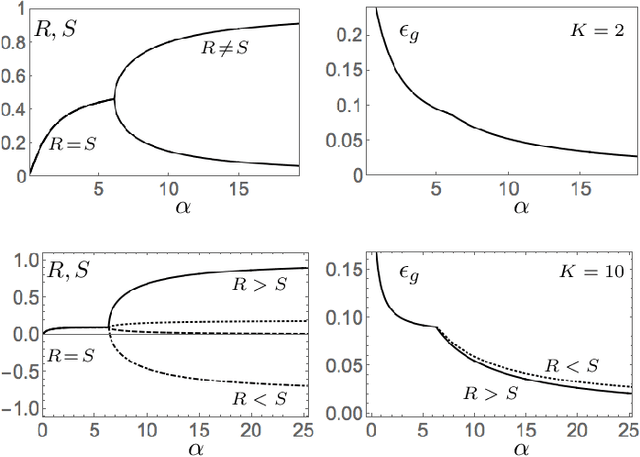
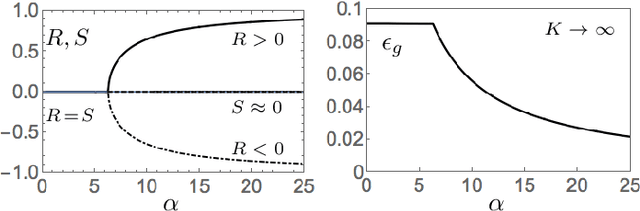
We study layered neural networks of rectified linear units (ReLU) in a modelling framework for stochastic training processes. The comparison with sigmoidal activation functions is in the center of interest. We compute typical learning curves for shallow networks with K hidden units in matching student teacher scenarios. The systems exhibit sudden changes of the generalization performance via the process of hidden unit specialization at critical sizes of the training set. Surprisingly, our results show that the training behavior of ReLU networks is qualitatively different from that of networks with sigmoidal activations. In networks with K >= 3 sigmoidal hidden units, the transition is discontinuous: Specialized network configurations co-exist and compete with states of poor performance even for very large training sets. On the contrary, the use of ReLU activations results in continuous transitions for all K: For large enough training sets, two competing, differently specialized states display similar generalization abilities, which coincide exactly for large networks in the limit K to infinity.

Galaxy classification: A machine learning analysis of GAMA catalogue data

We present a machine learning analysis of five labelled galaxy catalogues from the Galaxy And Mass Assembly (GAMA): The SersicCatVIKING and SersicCatUKIDSS catalogues containing morphological features, the GaussFitSimple catalogue containing spectroscopic features, the MagPhys catalogue including physical parameters for galaxies, and the Lambdar catalogue, which contains photometric measurements. Extending work previously presented at the ESANN 2018 conference - in an analysis based on Generalized Relevance Matrix Learning Vector Quantization and Random Forests - we find that neither the data from the individual catalogues nor a combined dataset based on all 5 catalogues fully supports the visual-inspection-based galaxy classification scheme employed to categorise the galaxies. In particular, only one class, the Little Blue Spheroids, is consistently separable from the other classes. To aid further insight into the nature of the employed visual-based classification scheme with respect to physical and morphological features, we present the galaxy parameters that are discriminative for the achieved class distinctions.

On-line learning dynamics of ReLU neural networks using statistical physics techniques

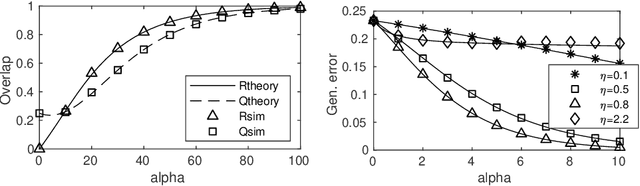
We introduce exact macroscopic on-line learning dynamics of two-layer neural networks with ReLU units in the form of a system of differential equations, using techniques borrowed from statistical physics. For the first experiments, numerical solutions reveal similar behavior compared to sigmoidal activation researched in earlier work. In these experiments the theoretical results show good correspondence with simulations. In ove-rrealizable and unrealizable learning scenarios, the learning behavior of ReLU networks shows distinctive characteristics compared to sigmoidal networks.

Prototype-based classifiers in the presence of concept drift: A modelling framework

We present a modelling framework for the investigation of prototype-based classifiers in non-stationary environments. Specifically, we study Learning Vector Quantization (LVQ) systems trained from a stream of high-dimensional, clustered data.We consider standard winner-takes-all updates known as LVQ1. Statistical properties of the input data change on the time scale defined by the training process. We apply analytical methods borrowed from statistical physics which have been used earlier for the exact description of learning in stationary environments. The suggested framework facilitates the computation of learning curves in the presence of virtual and real concept drift. Here we focus on timedependent class bias in the training data. First results demonstrate that, while basic LVQ algorithms are suitable for the training in non-stationary environments, weight decay as an explicit mechanism of forgetting does not improve the performance under the considered drift processes.