On the importance of structural identifiability for machine learning with partially observed dynamical systems

The successful application of modern machine learning for time series classification is often hampered by limitations in quality and quantity of available training data. To overcome these limitations, available domain expert knowledge in the form of parametrised mechanistic dynamical models can be used whenever it is available and time series observations may be represented as an element from a given class of parametrised dynamical models. This makes the learning process interpretable and allows the modeller to deal with sparsely and irregularly sampled data in a natural way. However, the internal processes of a dynamical model are often only partially observed. This can lead to ambiguity regarding which particular model realization best explains a given time series observation. This problem is well-known in the literature, and a dynamical model with this issue is referred to as structurally unidentifiable. Training a classifier that incorporates knowledge about a structurally unidentifiable dynamical model can negatively influence classification performance. To address this issue, we employ structural identifiability analysis to explicitly relate parameter configurations that are associated with identical system outputs. Using the derived relations in classifier training, we demonstrate that this method significantly improves the classifier's ability to generalize to unseen data on a number of example models from the biomedical domain. This effect is especially pronounced when the number of training instances is limited. Our results demonstrate the importance of accounting for structural identifiability, a topic that has received relatively little attention from the machine learning community.

Hidden Unit Specialization in Layered Neural Networks: ReLU vs. Sigmoidal Activation

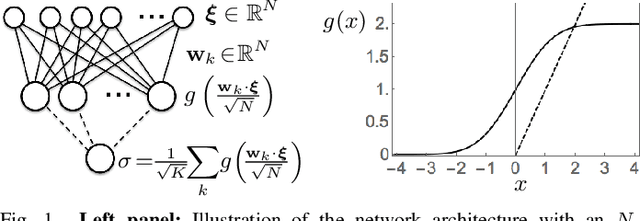
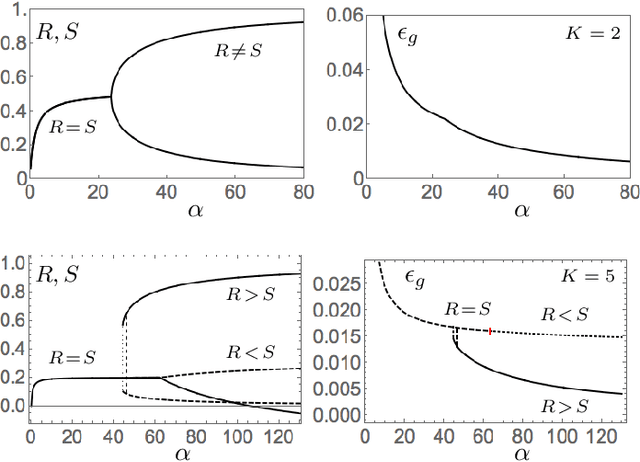
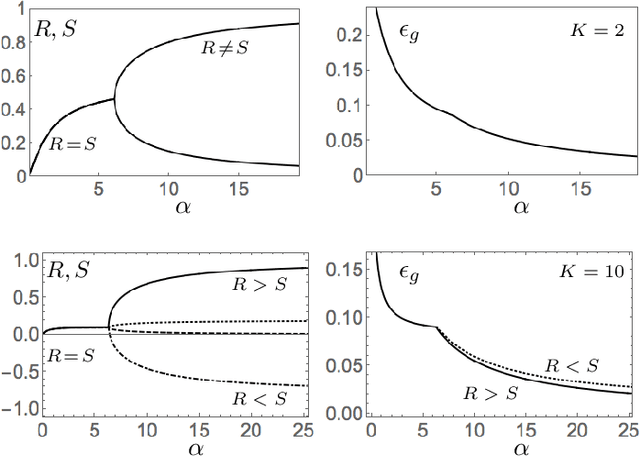
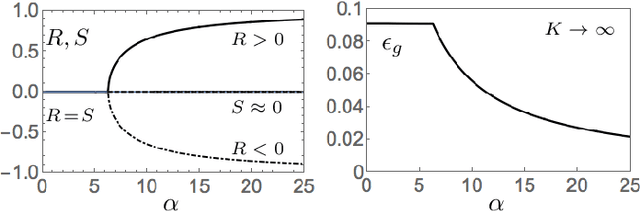
We study layered neural networks of rectified linear units (ReLU) in a modelling framework for stochastic training processes. The comparison with sigmoidal activation functions is in the center of interest. We compute typical learning curves for shallow networks with K hidden units in matching student teacher scenarios. The systems exhibit sudden changes of the generalization performance via the process of hidden unit specialization at critical sizes of the training set. Surprisingly, our results show that the training behavior of ReLU networks is qualitatively different from that of networks with sigmoidal activations. In networks with K >= 3 sigmoidal hidden units, the transition is discontinuous: Specialized network configurations co-exist and compete with states of poor performance even for very large training sets. On the contrary, the use of ReLU activations results in continuous transitions for all K: For large enough training sets, two competing, differently specialized states display similar generalization abilities, which coincide exactly for large networks in the limit K to infinity.