SAM-kNN Regressor for Online Learning in Water Distribution Networks

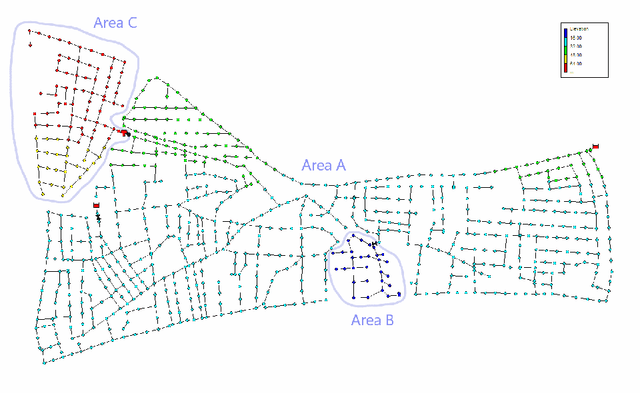
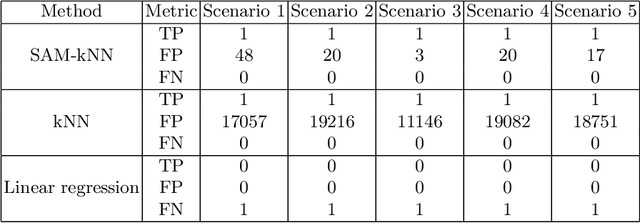
Water distribution networks are a key component of modern infrastructure for housing and industry. They transport and distribute water via widely branched networks from sources to consumers. In order to guarantee a working network at all times, the water supply company continuously monitors the network and takes actions when necessary -- e.g. reacting to leakages, sensor faults and drops in water quality. Since real world networks are too large and complex to be monitored by a human, algorithmic monitoring systems have been developed. A popular type of such systems are residual based anomaly detection systems that can detect events such as leakages and sensor faults. For a continuous high quality monitoring, it is necessary for these systems to adapt to changed demands and presence of various anomalies. In this work, we propose an adaption of the incremental SAM-kNN classifier for regression to build a residual based anomaly detection system for water distribution networks that is able to adapt to any kind of change.

Analysis of Drifting Features

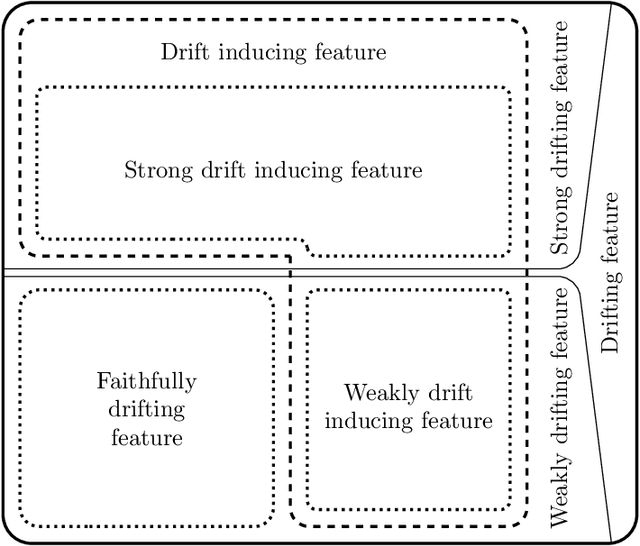
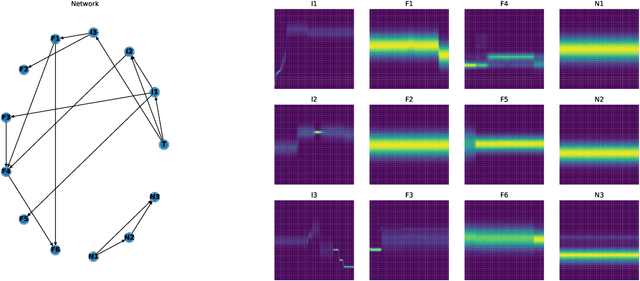
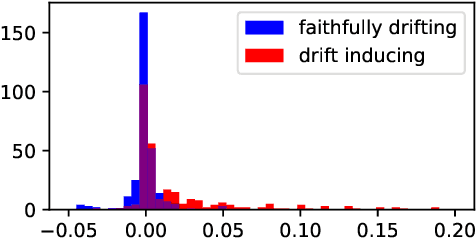
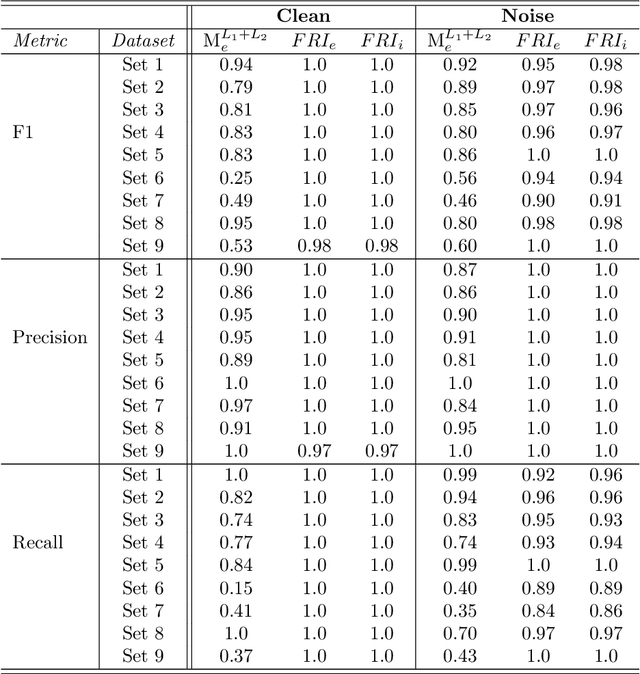
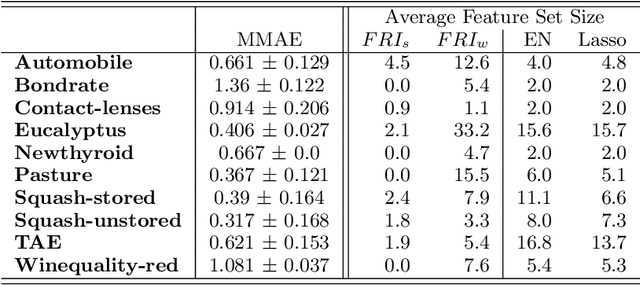
The notion of concept drift refers to the phenomenon that the distribution, which is underlying the observed data, changes over time. We are interested in an identification of those features, that are most relevant for the observed drift. We distinguish between drift inducing features, for which the observed feature drift cannot be explained by any other feature, and faithfully drifting features, which correlate with the present drift of other features. This notion gives rise to minimal subsets of the feature space, which are able to characterize the observed drift as a whole. We relate this problem to the problems of feature selection and feature relevance learning, which allows us to derive a detection algorithm. We demonstrate its usefulness on different benchmarks.

Feature Relevance Determination for Ordinal Regression in the Context of Feature Redundancies and Privileged Information

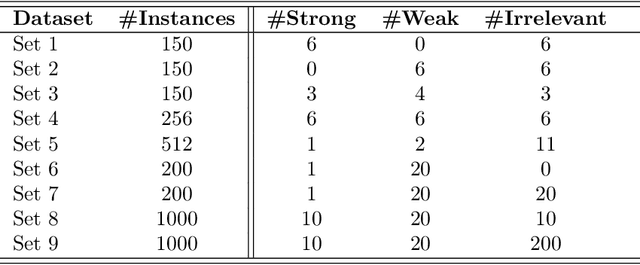
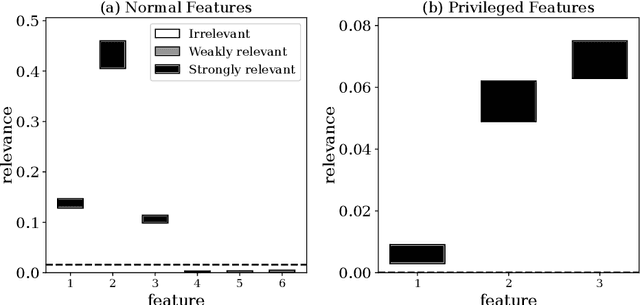
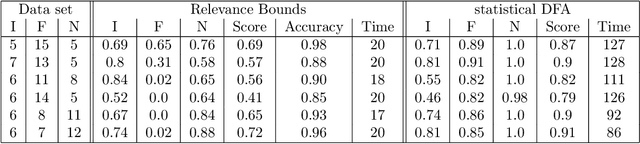
Advances in machine learning technologies have led to increasingly powerful models in particular in the context of big data. Yet, many application scenarios demand for robustly interpretable models rather than optimum model accuracy; as an example, this is the case if potential biomarkers or causal factors should be discovered based on a set of given measurements. In this contribution, we focus on feature selection paradigms, which enable us to uncover relevant factors of a given regularity based on a sparse model. We focus on the important specific setting of linear ordinal regression, i.e.\ data have to be ranked into one of a finite number of ordered categories by a linear projection. Unlike previous work, we consider the case that features are potentially redundant, such that no unique minimum set of relevant features exists. We aim for an identification of all strongly and all weakly relevant features as well as their type of relevance (strong or weak); we achieve this goal by determining feature relevance bounds, which correspond to the minimum and maximum feature relevance, respectively, if searched over all equivalent models. In addition, we discuss how this setting enables us to substitute some of the features, e.g.\ due to their semantics, and how to extend the framework of feature relevance intervals to the setting of privileged information, i.e.\ potentially relevant information is available for training purposes only, but cannot be used for the prediction itself.

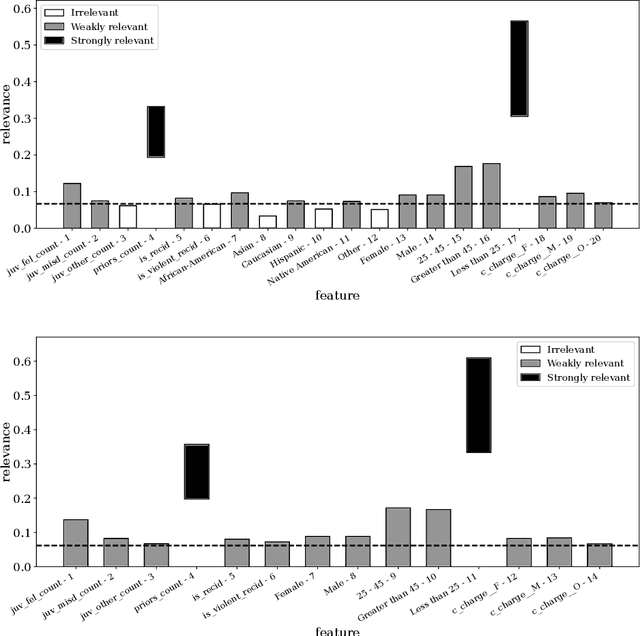
Feature Relevance Bounds for Ordinal Regression

The increasing occurrence of ordinal data, mainly sociodemographic, led to a renewed research interest in ordinal regression, i.e. the prediction of ordered classes. Besides model accuracy, the interpretation of these models itself is of high relevance, and existing approaches therefore enforce e.g. model sparsity. For high dimensional or highly correlated data, however, this might be misleading due to strong variable dependencies. In this contribution, we aim for an identification of feature relevance bounds which - besides identifying all relevant features - explicitly differentiates between strongly and weakly relevant features.