Feature Relevance Determination for Ordinal Regression in the Context of Feature Redundancies and Privileged Information
Paper and Code
Dec 10, 2019
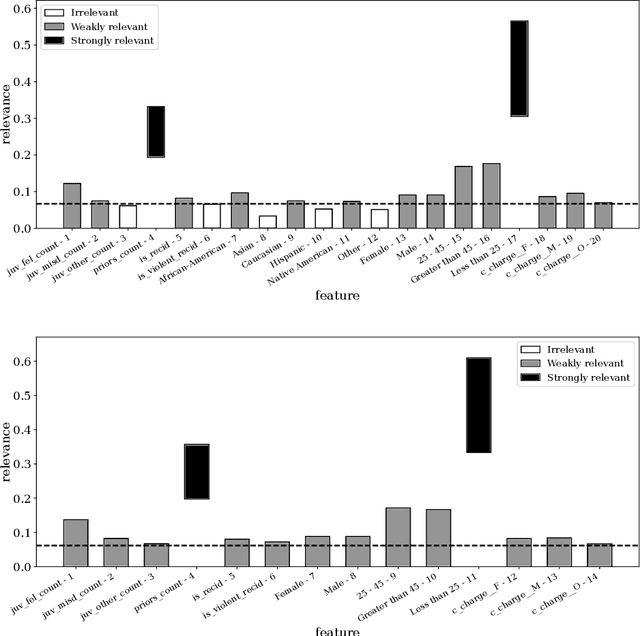
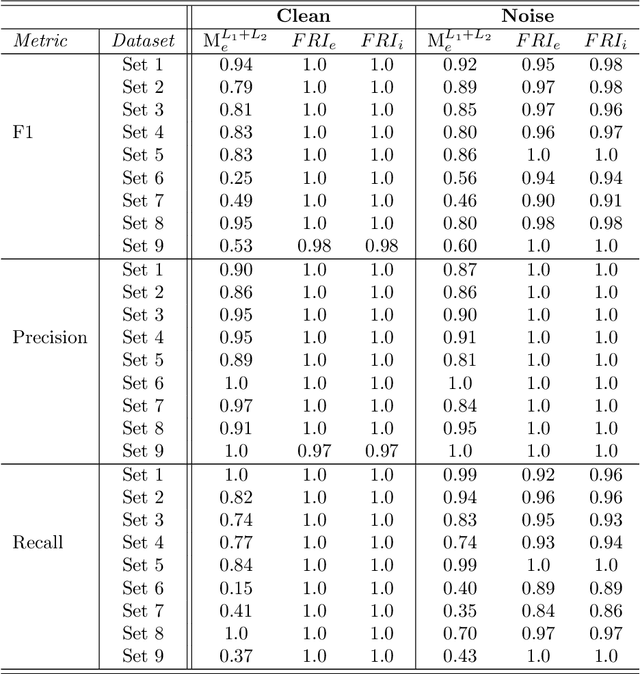
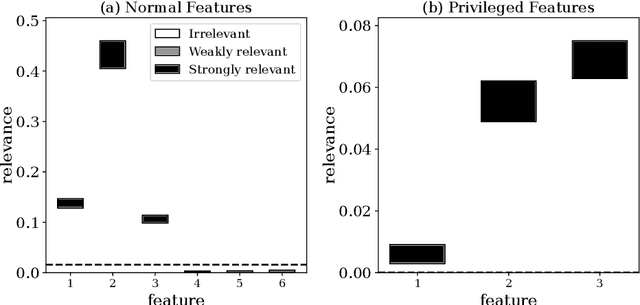
Advances in machine learning technologies have led to increasingly powerful models in particular in the context of big data. Yet, many application scenarios demand for robustly interpretable models rather than optimum model accuracy; as an example, this is the case if potential biomarkers or causal factors should be discovered based on a set of given measurements. In this contribution, we focus on feature selection paradigms, which enable us to uncover relevant factors of a given regularity based on a sparse model. We focus on the important specific setting of linear ordinal regression, i.e.\ data have to be ranked into one of a finite number of ordered categories by a linear projection. Unlike previous work, we consider the case that features are potentially redundant, such that no unique minimum set of relevant features exists. We aim for an identification of all strongly and all weakly relevant features as well as their type of relevance (strong or weak); we achieve this goal by determining feature relevance bounds, which correspond to the minimum and maximum feature relevance, respectively, if searched over all equivalent models. In addition, we discuss how this setting enables us to substitute some of the features, e.g.\ due to their semantics, and how to extend the framework of feature relevance intervals to the setting of privileged information, i.e.\ potentially relevant information is available for training purposes only, but cannot be used for the prediction itself.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge