Efficient Cross-Domain Federated Learning by MixStyle Approximation

With the advent of interconnected and sensor-equipped edge devices, Federated Learning (FL) has gained significant attention, enabling decentralized learning while maintaining data privacy. However, FL faces two challenges in real-world tasks: expensive data labeling and domain shift between source and target samples. In this paper, we introduce a privacy-preserving, resource-efficient FL concept for client adaptation in hardware-constrained environments. Our approach includes server model pre-training on source data and subsequent fine-tuning on target data via low-end clients. The local client adaptation process is streamlined by probabilistic mixing of instance-level feature statistics approximated from source and target domain data. The adapted parameters are transferred back to the central server and globally aggregated. Preliminary results indicate that our method reduces computational and transmission costs while maintaining competitive performance on downstream tasks.

Revisiting Memory Efficient Kernel Approximation: An Indefinite Learning Perspective

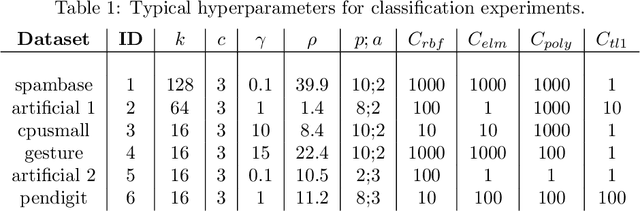
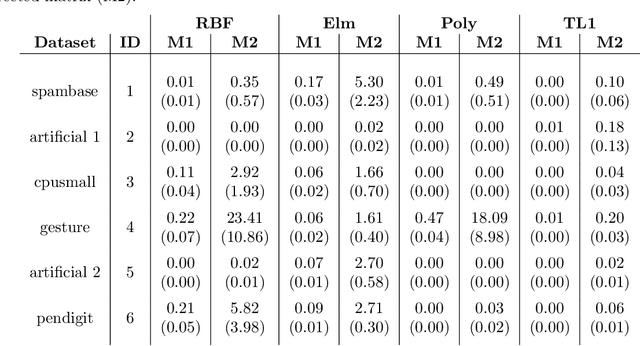
Matrix approximations are a key element in large-scale algebraic machine learning approaches. The recently proposed method MEKA (Si et al., 2014) effectively employs two common assumptions in Hilbert spaces: the low-rank property of an inner product matrix obtained from a shift-invariant kernel function and a data compactness hypothesis by means of an inherent block-cluster structure. In this work, we extend MEKA to be applicable not only for shift-invariant kernels but also for non-stationary kernels like polynomial kernels and an extreme learning kernel. We also address in detail how to handle non-positive semi-definite kernel functions within MEKA, either caused by the approximation itself or by the intentional use of general kernel functions. We present a Lanczos-based estimation of a spectrum shift to develop a stable positive semi-definite MEKA approximation, also usable in classical convex optimization frameworks. Furthermore, we support our findings with theoretical considerations and a variety of experiments on synthetic and real-world data.

Complex-valued embeddings of generic proximity data

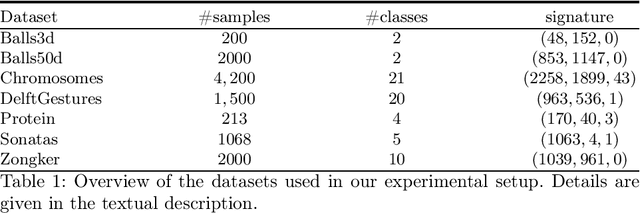
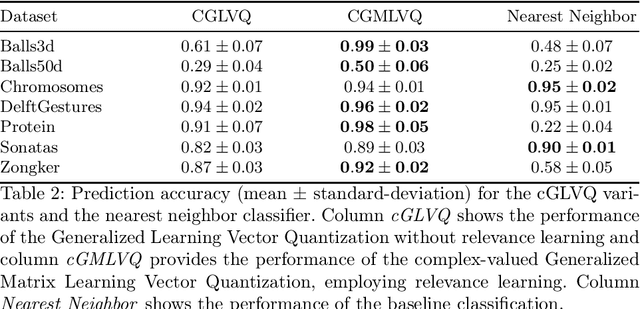
Proximities are at the heart of almost all machine learning methods. If the input data are given as numerical vectors of equal lengths, euclidean distance, or a Hilbertian inner product is frequently used in modeling algorithms. In a more generic view, objects are compared by a (symmetric) similarity or dissimilarity measure, which may not obey particular mathematical properties. This renders many machine learning methods invalid, leading to convergence problems and the loss of guarantees, like generalization bounds. In many cases, the preferred dissimilarity measure is not metric, like the earth mover distance, or the similarity measure may not be a simple inner product in a Hilbert space but in its generalization a Krein space. If the input data are non-vectorial, like text sequences, proximity-based learning is used or ngram embedding techniques can be applied. Standard embeddings lead to the desired fixed-length vector encoding, but are costly and have substantial limitations in preserving the original data's full information. As an information preserving alternative, we propose a complex-valued vector embedding of proximity data. This allows suitable machine learning algorithms to use these fixed-length, complex-valued vectors for further processing. The complex-valued data can serve as an input to complex-valued machine learning algorithms. In particular, we address supervised learning and use extensions of prototype-based learning. The proposed approach is evaluated on a variety of standard benchmarks and shows strong performance compared to traditional techniques in processing non-metric or non-psd proximity data.