Injecting Hamiltonian Architectural Bias into Deep Graph Networks for Long-Range Propagation

The dynamics of information diffusion within graphs is a critical open issue that heavily influences graph representation learning, especially when considering long-range propagation. This calls for principled approaches that control and regulate the degree of propagation and dissipation of information throughout the neural flow. Motivated by this, we introduce (port-)Hamiltonian Deep Graph Networks, a novel framework that models neural information flow in graphs by building on the laws of conservation of Hamiltonian dynamical systems. We reconcile under a single theoretical and practical framework both non-dissipative long-range propagation and non-conservative behaviors, introducing tools from mechanical systems to gauge the equilibrium between the two components. Our approach can be applied to general message-passing architectures, and it provides theoretical guarantees on information conservation in time. Empirical results prove the effectiveness of our port-Hamiltonian scheme in pushing simple graph convolutional architectures to state-of-the-art performance in long-range benchmarks.

Revisiting Memory Efficient Kernel Approximation: An Indefinite Learning Perspective

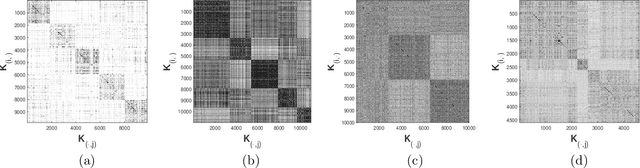
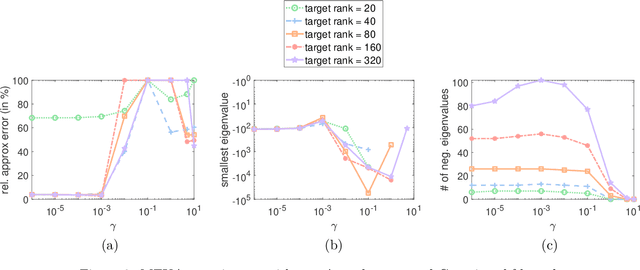
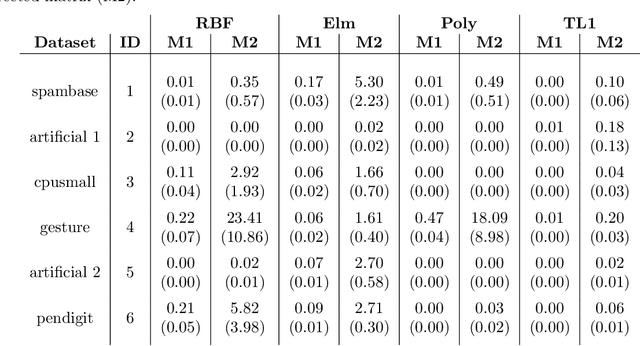
Matrix approximations are a key element in large-scale algebraic machine learning approaches. The recently proposed method MEKA (Si et al., 2014) effectively employs two common assumptions in Hilbert spaces: the low-rank property of an inner product matrix obtained from a shift-invariant kernel function and a data compactness hypothesis by means of an inherent block-cluster structure. In this work, we extend MEKA to be applicable not only for shift-invariant kernels but also for non-stationary kernels like polynomial kernels and an extreme learning kernel. We also address in detail how to handle non-positive semi-definite kernel functions within MEKA, either caused by the approximation itself or by the intentional use of general kernel functions. We present a Lanczos-based estimation of a spectrum shift to develop a stable positive semi-definite MEKA approximation, also usable in classical convex optimization frameworks. Furthermore, we support our findings with theoretical considerations and a variety of experiments on synthetic and real-world data.