Return of ChebNet: Understanding and Improving an Overlooked GNN on Long Range Tasks

ChebNet, one of the earliest spectral GNNs, has largely been overshadowed by Message Passing Neural Networks (MPNNs), which gained popularity for their simplicity and effectiveness in capturing local graph structure. Despite their success, MPNNs are limited in their ability to capture long-range dependencies between nodes. This has led researchers to adapt MPNNs through rewiring or make use of Graph Transformers, which compromises the computational efficiency that characterized early spatial message-passing architectures, and typically disregards the graph structure. Almost a decade after its original introduction, we revisit ChebNet to shed light on its ability to model distant node interactions. We find that out-of-box, ChebNet already shows competitive advantages relative to classical MPNNs and GTs on long-range benchmarks, while maintaining good scalability properties for high-order polynomials. However, we uncover that this polynomial expansion leads ChebNet to an unstable regime during training. To address this limitation, we cast ChebNet as a stable and non-dissipative dynamical system, which we coin Stable-ChebNet. Our Stable-ChebNet model allows for stable information propagation, and has controllable dynamics which do not require the use of eigendecompositions, positional encodings, or graph rewiring. Across several benchmarks, Stable-ChebNet achieves near state-of-the-art performance.

Message-Passing State-Space Models: Improving Graph Learning with Modern Sequence Modeling

The recent success of State-Space Models (SSMs) in sequence modeling has motivated their adaptation to graph learning, giving rise to Graph State-Space Models (GSSMs). However, existing GSSMs operate by applying SSM modules to sequences extracted from graphs, often compromising core properties such as permutation equivariance, message-passing compatibility, and computational efficiency. In this paper, we introduce a new perspective by embedding the key principles of modern SSM computation directly into the Message-Passing Neural Network framework, resulting in a unified methodology for both static and temporal graphs. Our approach, MP-SSM, enables efficient, permutation-equivariant, and long-range information propagation while preserving the architectural simplicity of message passing. Crucially, MP-SSM enables an exact sensitivity analysis, which we use to theoretically characterize information flow and evaluate issues like vanishing gradients and over-squashing in the deep regime. Furthermore, our design choices allow for a highly optimized parallel implementation akin to modern SSMs. We validate MP-SSM across a wide range of tasks, including node classification, graph property prediction, long-range benchmarks, and spatiotemporal forecasting, demonstrating both its versatility and strong empirical performance.

Information propagation dynamics in Deep Graph Networks

Graphs are a highly expressive abstraction for modeling entities and their relations, such as molecular structures, social networks, and traffic networks. Deep Graph Networks (DGNs) have emerged as a family of deep learning models that can effectively process and learn such structured information. However, learning effective information propagation patterns within DGNs remains a critical challenge that heavily influences the model capabilities, both in the static domain and in the temporal domain (where features and/or topology evolve). Given this challenge, this thesis investigates the dynamics of information propagation within DGNs for static and dynamic graphs, focusing on their design as dynamical systems. Throughout this work, we provide theoretical and empirical evidence to demonstrate the effectiveness of our proposed architectures in propagating and preserving long-term dependencies between nodes, and in learning complex spatio-temporal patterns from irregular and sparsely sampled dynamic graphs. In summary, this thesis provides a comprehensive exploration of the intersection between graphs, deep learning, and dynamical systems, offering insights and advancements for the field of graph representation learning and paving the way for more effective and versatile graph-based learning models.

Long Range Propagation on Continuous-Time Dynamic Graphs

Learning Continuous-Time Dynamic Graphs (C-TDGs) requires accurately modeling spatio-temporal information on streams of irregularly sampled events. While many methods have been proposed recently, we find that most message passing-, recurrent- or self-attention-based methods perform poorly on long-range tasks. These tasks require correlating information that occurred "far" away from the current event, either spatially (higher-order node information) or along the time dimension (events occurred in the past). To address long-range dependencies, we introduce Continuous-Time Graph Anti-Symmetric Network (CTAN). Grounded within the ordinary differential equations framework, our method is designed for efficient propagation of information. In this paper, we show how CTAN's (i) long-range modeling capabilities are substantiated by theoretical findings and how (ii) its empirical performance on synthetic long-range benchmarks and real-world benchmarks is superior to other methods. Our results motivate CTAN's ability to propagate long-range information in C-TDGs as well as the inclusion of long-range tasks as part of temporal graph models evaluation.

Injecting Hamiltonian Architectural Bias into Deep Graph Networks for Long-Range Propagation

The dynamics of information diffusion within graphs is a critical open issue that heavily influences graph representation learning, especially when considering long-range propagation. This calls for principled approaches that control and regulate the degree of propagation and dissipation of information throughout the neural flow. Motivated by this, we introduce (port-)Hamiltonian Deep Graph Networks, a novel framework that models neural information flow in graphs by building on the laws of conservation of Hamiltonian dynamical systems. We reconcile under a single theoretical and practical framework both non-dissipative long-range propagation and non-conservative behaviors, introducing tools from mechanical systems to gauge the equilibrium between the two components. Our approach can be applied to general message-passing architectures, and it provides theoretical guarantees on information conservation in time. Empirical results prove the effectiveness of our port-Hamiltonian scheme in pushing simple graph convolutional architectures to state-of-the-art performance in long-range benchmarks.

Tackling Graph Oversquashing by Global and Local Non-Dissipativity

A common problem in Message-Passing Neural Networks is oversquashing -- the limited ability to facilitate effective information flow between distant nodes. Oversquashing is attributed to the exponential decay in information transmission as node distances increase. This paper introduces a novel perspective to address oversquashing, leveraging properties of global and local non-dissipativity, that enable the maintenance of a constant information flow rate. Namely, we present SWAN, a uniquely parameterized model GNN with antisymmetry both in space and weight domains, as a means to obtain non-dissipativity. Our theoretical analysis asserts that by achieving these properties, SWAN offers an enhanced ability to transmit information over extended distances. Empirical evaluations on synthetic and real-world benchmarks that emphasize long-range interactions validate the theoretical understanding of SWAN, and its ability to mitigate oversquashing.

Temporal Graph ODEs for Irregularly-Sampled Time Series

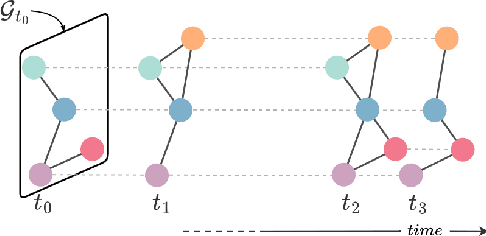
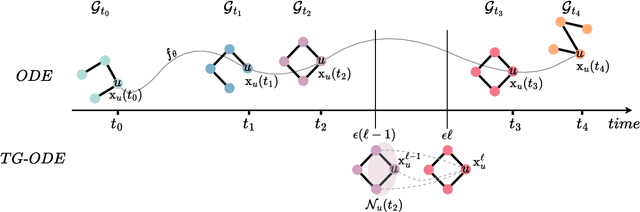
Modern graph representation learning works mostly under the assumption of dealing with regularly sampled temporal graph snapshots, which is far from realistic, e.g., social networks and physical systems are characterized by continuous dynamics and sporadic observations. To address this limitation, we introduce the Temporal Graph Ordinary Differential Equation (TG-ODE) framework, which learns both the temporal and spatial dynamics from graph streams where the intervals between observations are not regularly spaced. We empirically validate the proposed approach on several graph benchmarks, showing that TG-ODE can achieve state-of-the-art performance in irregular graph stream tasks.

Deep learning for dynamic graphs: models and benchmarks

Recent progress in research on Deep Graph Networks (DGNs) has led to a maturation of the domain of learning on graphs. Despite the growth of this research field, there are still important challenges that are yet unsolved. Specifically, there is an urge of making DGNs suitable for predictive tasks on realworld systems of interconnected entities, which evolve over time. With the aim of fostering research in the domain of dynamic graphs, at first, we survey recent advantages in learning both temporal and spatial information, providing a comprehensive overview of the current state-of-the-art in the domain of representation learning for dynamic graphs. Secondly, we conduct a fair performance comparison among the most popular proposed approaches, leveraging rigorous model selection and assessment for all the methods, thus establishing a sound baseline for evaluating new architectures and approaches

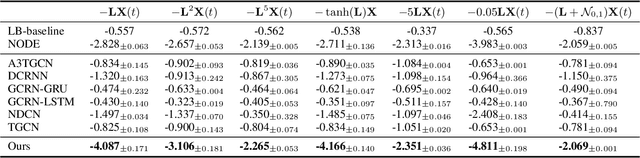
Anti-Symmetric DGN: a stable architecture for Deep Graph Networks

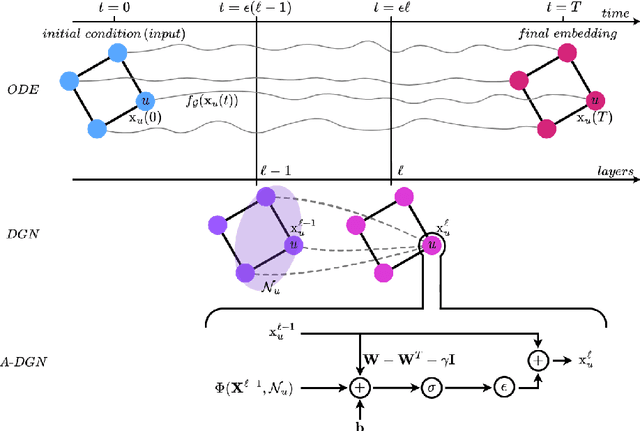
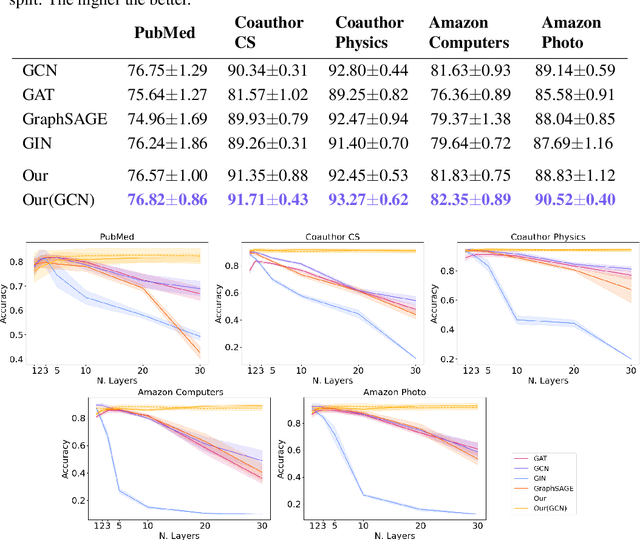
Deep Graph Networks (DGNs) currently dominate the research landscape of learning from graphs, due to their efficiency and ability to implement an adaptive message-passing scheme between the nodes. However, DGNs are typically limited in their ability to propagate and preserve long-term dependencies between nodes, \ie they suffer from the over-squashing phenomena. This reduces their effectiveness, since predictive problems may require to capture interactions at different, and possibly large, radii in order to be effectively solved. In this work, we present Anti-Symmetric Deep Graph Networks (A-DGNs), a framework for stable and non-dissipative DGN design, conceived through the lens of ordinary differential equations. We give theoretical proof that our method is stable and non-dissipative, leading to two key results: long-range information between nodes is preserved, and no gradient vanishing or explosion occurs in training. We empirically validate the proposed approach on several graph benchmarks, showing that A-DGN yields to improved performance and enables to learn effectively even when dozens of layers are used.