Learning Latent Graph Structures and their Uncertainty

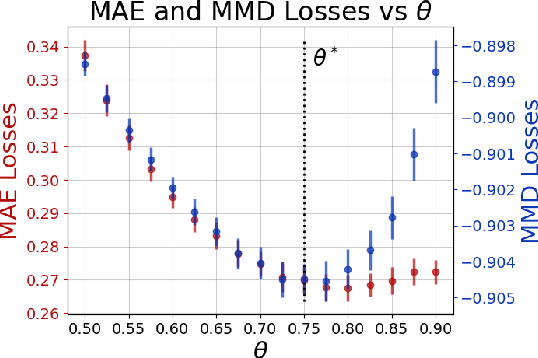
Within a prediction task, Graph Neural Networks (GNNs) use relational information as an inductive bias to enhance the model's accuracy. As task-relevant relations might be unknown, graph structure learning approaches have been proposed to learn them while solving the downstream prediction task. In this paper, we demonstrate that minimization of a point-prediction loss function, e.g., the mean absolute error, does not guarantee proper learning of the latent relational information and its associated uncertainty. Conversely, we prove that a suitable loss function on the stochastic model outputs simultaneously grants (i) the unknown adjacency matrix latent distribution and (ii) optimal performance on the prediction task. Finally, we propose a sampling-based method that solves this joint learning task. Empirical results validate our theoretical claims and demonstrate the effectiveness of the proposed approach.

Temporal Graph ODEs for Irregularly-Sampled Time Series

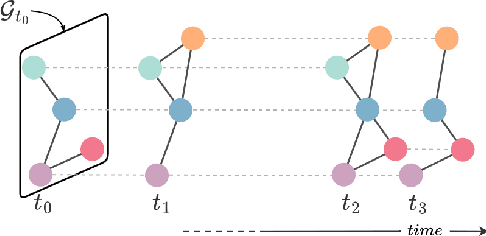
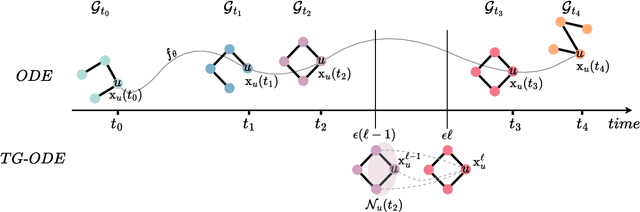
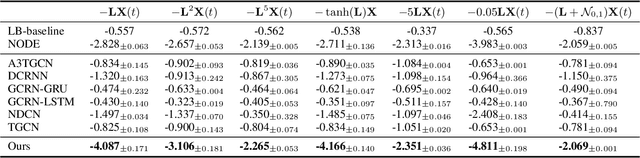
Modern graph representation learning works mostly under the assumption of dealing with regularly sampled temporal graph snapshots, which is far from realistic, e.g., social networks and physical systems are characterized by continuous dynamics and sporadic observations. To address this limitation, we introduce the Temporal Graph Ordinary Differential Equation (TG-ODE) framework, which learns both the temporal and spatial dynamics from graph streams where the intervals between observations are not regularly spaced. We empirically validate the proposed approach on several graph benchmarks, showing that TG-ODE can achieve state-of-the-art performance in irregular graph stream tasks.

Graph-based Virtual Sensing from Sparse and Partial Multivariate Observations

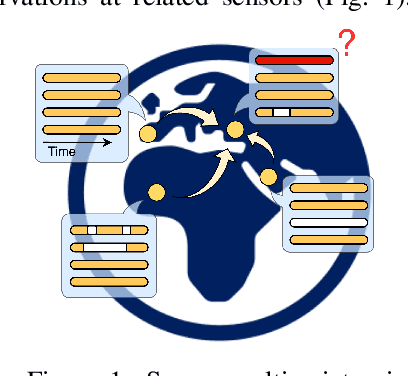
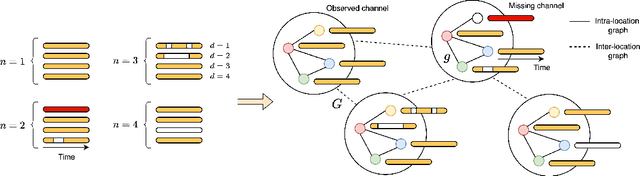
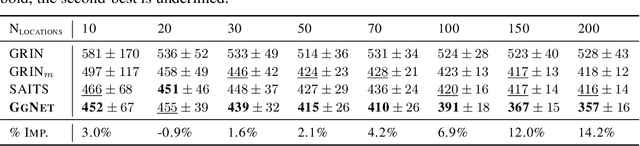
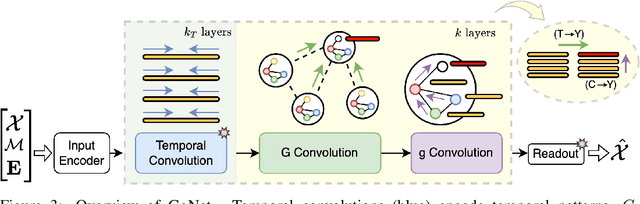
Virtual sensing techniques allow for inferring signals at new unmonitored locations by exploiting spatio-temporal measurements coming from physical sensors at different locations. However, as the sensor coverage becomes sparse due to costs or other constraints, physical proximity cannot be used to support interpolation. In this paper, we overcome this challenge by leveraging dependencies between the target variable and a set of correlated variables (covariates) that can frequently be associated with each location of interest. From this viewpoint, covariates provide partial observability, and the problem consists of inferring values for unobserved channels by exploiting observations at other locations to learn how such variables can correlate. We introduce a novel graph-based methodology to exploit such relationships and design a graph deep learning architecture, named GgNet, implementing the framework. The proposed approach relies on propagating information over a nested graph structure that is used to learn dependencies between variables as well as locations. GgNet is extensively evaluated under different virtual sensing scenarios, demonstrating higher reconstruction accuracy compared to the state-of-the-art.

Graph Deep Learning for Time Series Forecasting

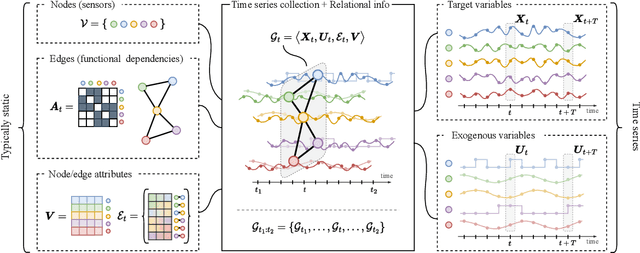
Graph-based deep learning methods have become popular tools to process collections of correlated time series. Differently from traditional multivariate forecasting methods, neural graph-based predictors take advantage of pairwise relationships by conditioning forecasts on a (possibly dynamic) graph spanning the time series collection. The conditioning can take the form of an architectural inductive bias on the neural forecasting architecture, resulting in a family of deep learning models called spatiotemporal graph neural networks. Such relational inductive biases enable the training of global forecasting models on large time-series collections, while at the same time localizing predictions w.r.t. each element in the set (i.e., graph nodes) by accounting for local correlations among them (i.e., graph edges). Indeed, recent theoretical and practical advances in graph neural networks and deep learning for time series forecasting make the adoption of such processing frameworks appealing and timely. However, most of the studies in the literature focus on proposing variations of existing neural architectures by taking advantage of modern deep learning practices, while foundational and methodological aspects have not been subject to systematic investigation. To fill the gap, this paper aims to introduce a comprehensive methodological framework that formalizes the forecasting problem and provides design principles for graph-based predictive models and methods to assess their performance. At the same time, together with an overview of the field, we provide design guidelines, recommendations, and best practices, as well as an in-depth discussion of open challenges and future research directions.

A Survey on Graph Neural Networks for Time Series: Forecasting, Classification, Imputation, and Anomaly Detection

Time series are the primary data type used to record dynamic system measurements and generated in great volume by both physical sensors and online processes (virtual sensors). Time series analytics is therefore crucial to unlocking the wealth of information implicit in available data. With the recent advancements in graph neural networks (GNNs), there has been a surge in GNN-based approaches for time series analysis. Approaches can explicitly model inter-temporal and inter-variable relationships, which traditional and other deep neural network-based methods struggle to do. In this survey, we provide a comprehensive review of graph neural networks for time series analysis (GNN4TS), encompassing four fundamental dimensions: Forecasting, classification, anomaly detection, and imputation. Our aim is to guide designers and practitioners to understand, build applications, and advance research of GNN4TS. At first, we provide a comprehensive task-oriented taxonomy of GNN4TS. Then, we present and discuss representative research works and, finally, discuss mainstream applications of GNN4TS. A comprehensive discussion of potential future research directions completes the survey. This survey, for the first time, brings together a vast array of knowledge on GNN-based time series research, highlighting both the foundations, practical applications, and opportunities of graph neural networks for time series analysis.

Graph Kalman Filters

The well-known Kalman filters model dynamical systems by relying on state-space representations with the next state updated, and its uncertainty controlled, by fresh information associated with newly observed system outputs. This paper generalizes, for the first time in the literature, Kalman and extended Kalman filters to discrete-time settings where inputs, states, and outputs are represented as attributed graphs whose topology and attributes can change with time. The setup allows us to adapt the framework to cases where the output is a vector or a scalar too (node/graph level tasks). Within the proposed theoretical framework, the unknown state-transition and the readout functions are learned end-to-end along with the downstream prediction task.

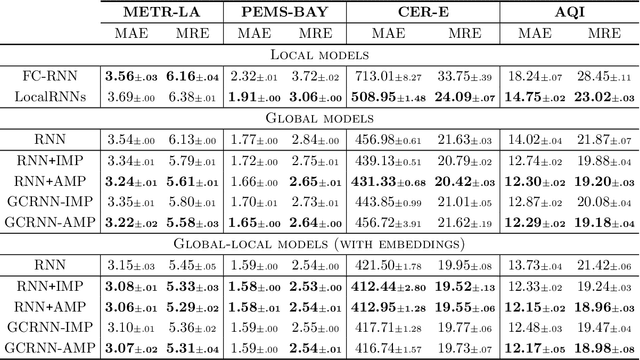
Taming Local Effects in Graph-based Spatiotemporal Forecasting

Spatiotemporal graph neural networks have shown to be effective in time series forecasting applications, achieving better performance than standard univariate predictors in several settings. These architectures take advantage of a graph structure and relational inductive biases to learn a single (global) inductive model to predict any number of the input time series, each associated with a graph node. Despite the gain achieved in computational and data efficiency w.r.t. fitting a set of local models, relying on a single global model can be a limitation whenever some of the time series are generated by a different spatiotemporal stochastic process. The main objective of this paper is to understand the interplay between globality and locality in graph-based spatiotemporal forecasting, while contextually proposing a methodological framework to rationalize the practice of including trainable node embeddings in such architectures. We ascribe to trainable node embeddings the role of amortizing the learning of specialized components. Moreover, embeddings allow for 1) effectively combining the advantages of shared message-passing layers with node-specific parameters and 2) efficiently transferring the learned model to new node sets. Supported by strong empirical evidence, we provide insights and guidelines for specializing graph-based models to the dynamics of each time series and show how this aspect plays a crucial role in obtaining accurate predictions.

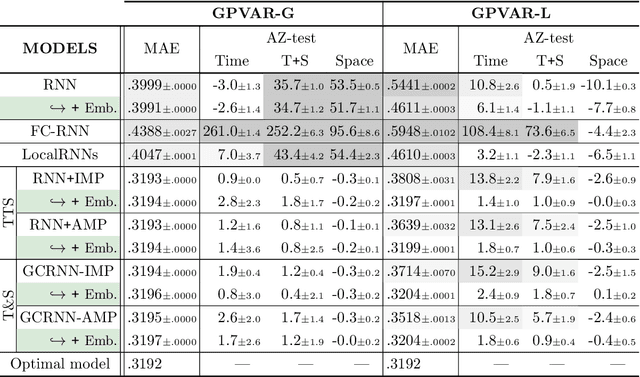
Where and How to Improve Graph-based Spatio-temporal Predictors

This paper introduces a novel residual correlation analysis, called AZ-analysis, to assess the optimality of spatio-temporal predictive models. The proposed AZ-analysis constitutes a valuable asset for discovering and highlighting those space-time regions where the model can be improved with respect to performance. The AZ-analysis operates under very mild assumptions and is based on a spatio-temporal graph that encodes serial and functional dependencies in the data; asymptotically distribution-free summary statistics identify existing residual correlation in space and time regions, hence localizing time frames and/or communities of sensors, where the predictor can be improved.

Graph state-space models

State-space models constitute an effective modeling tool to describe multivariate time series and operate by maintaining an updated representation of the system state from which predictions are made. Within this framework, relational inductive biases, e.g., associated with functional dependencies existing among signals, are not explicitly exploited leaving unattended great opportunities for effective modeling approaches. The manuscript aims, for the first time, at filling this gap by matching state-space modeling and spatio-temporal data where the relational information, say the functional graph capturing latent dependencies, is learned directly from data and is allowed to change over time. Within a probabilistic formulation that accounts for the uncertainty in the data-generating process, an encoder-decoder architecture is proposed to learn the state-space model end-to-end on a downstream task. The proposed methodological framework generalizes several state-of-the-art methods and demonstrates to be effective in extracting meaningful relational information while achieving optimal forecasting performance in controlled environments.

Sparse Graph Learning for Spatiotemporal Time Series

Outstanding achievements of graph neural networks for spatiotemporal time series prediction show that relational constraints introduce a positive inductive bias into neural forecasting architectures. Often, however, the relational information characterizing the underlying data generating process is unavailable; the practitioner is then left with the problem of inferring from data which relational graph to use in the subsequent processing stages. We propose novel, principled -- yet practical -- probabilistic methods that learn the relational dependencies by modeling distributions over graphs while maximizing, at the same time, end-to-end the forecasting accuracy. Our novel graph learning approach, based on consolidated variance reduction techniques for Monte Carlo score-based gradient estimation, is theoretically grounded and effective. We show that tailoring the gradient estimators to the graph learning problem allows us also for achieving state-of-the-art forecasting performance while controlling, at the same time, both the sparsity of the learned graph and the computational burden. We empirically assess the effectiveness of the proposed method on synthetic and real-world benchmarks, showing that the proposed solution can be used as a stand-alone graph identification procedure as well as a learned component of an end-to-end forecasting architecture.