Graph-based Forecasting with Missing Data through Spatiotemporal Downsampling

Given a set of synchronous time series, each associated with a sensor-point in space and characterized by inter-series relationships, the problem of spatiotemporal forecasting consists of predicting future observations for each point. Spatiotemporal graph neural networks achieve striking results by representing the relationships across time series as a graph. Nonetheless, most existing methods rely on the often unrealistic assumption that inputs are always available and fail to capture hidden spatiotemporal dynamics when part of the data is missing. In this work, we tackle this problem through hierarchical spatiotemporal downsampling. The input time series are progressively coarsened over time and space, obtaining a pool of representations that capture heterogeneous temporal and spatial dynamics. Conditioned on observations and missing data patterns, such representations are combined by an interpretable attention mechanism to generate the forecasts. Our approach outperforms state-of-the-art methods on synthetic and real-world benchmarks under different missing data distributions, particularly in the presence of contiguous blocks of missing values.

Graph Deep Learning for Time Series Forecasting

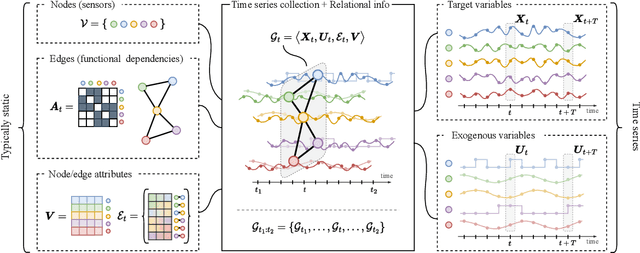
Graph-based deep learning methods have become popular tools to process collections of correlated time series. Differently from traditional multivariate forecasting methods, neural graph-based predictors take advantage of pairwise relationships by conditioning forecasts on a (possibly dynamic) graph spanning the time series collection. The conditioning can take the form of an architectural inductive bias on the neural forecasting architecture, resulting in a family of deep learning models called spatiotemporal graph neural networks. Such relational inductive biases enable the training of global forecasting models on large time-series collections, while at the same time localizing predictions w.r.t. each element in the set (i.e., graph nodes) by accounting for local correlations among them (i.e., graph edges). Indeed, recent theoretical and practical advances in graph neural networks and deep learning for time series forecasting make the adoption of such processing frameworks appealing and timely. However, most of the studies in the literature focus on proposing variations of existing neural architectures by taking advantage of modern deep learning practices, while foundational and methodological aspects have not been subject to systematic investigation. To fill the gap, this paper aims to introduce a comprehensive methodological framework that formalizes the forecasting problem and provides design principles for graph-based predictive models and methods to assess their performance. At the same time, together with an overview of the field, we provide design guidelines, recommendations, and best practices, as well as an in-depth discussion of open challenges and future research directions.

Taming Local Effects in Graph-based Spatiotemporal Forecasting

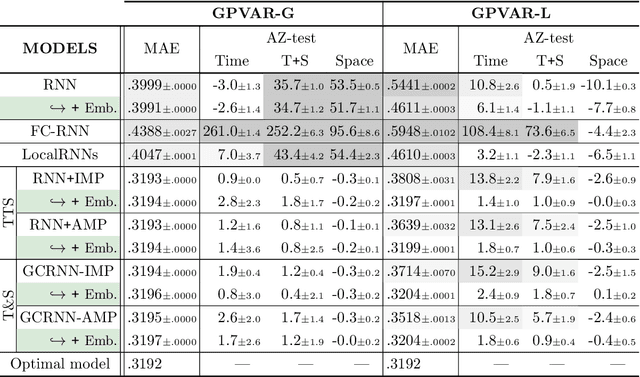
Spatiotemporal graph neural networks have shown to be effective in time series forecasting applications, achieving better performance than standard univariate predictors in several settings. These architectures take advantage of a graph structure and relational inductive biases to learn a single (global) inductive model to predict any number of the input time series, each associated with a graph node. Despite the gain achieved in computational and data efficiency w.r.t. fitting a set of local models, relying on a single global model can be a limitation whenever some of the time series are generated by a different spatiotemporal stochastic process. The main objective of this paper is to understand the interplay between globality and locality in graph-based spatiotemporal forecasting, while contextually proposing a methodological framework to rationalize the practice of including trainable node embeddings in such architectures. We ascribe to trainable node embeddings the role of amortizing the learning of specialized components. Moreover, embeddings allow for 1) effectively combining the advantages of shared message-passing layers with node-specific parameters and 2) efficiently transferring the learned model to new node sets. Supported by strong empirical evidence, we provide insights and guidelines for specializing graph-based models to the dynamics of each time series and show how this aspect plays a crucial role in obtaining accurate predictions.

Scalable Spatiotemporal Graph Neural Networks

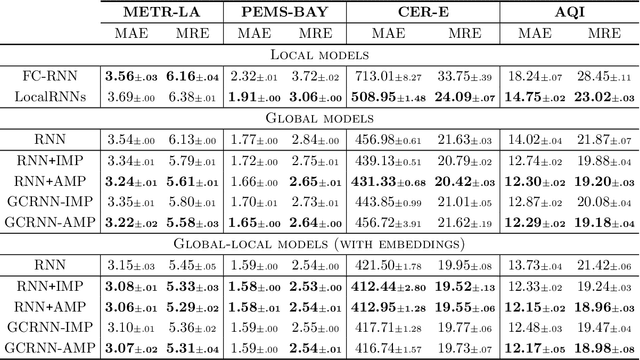
Neural forecasting of spatiotemporal time series drives both research and industrial innovation in several relevant application domains. Graph neural networks (GNNs) are often the core component of the forecasting architecture. However, in most spatiotemporal GNNs, the computational complexity scales up to a quadratic factor with the length of the sequence times the number of links in the graph, hence hindering the application of these models to large graphs and long temporal sequences. While methods to improve scalability have been proposed in the context of static graphs, few research efforts have been devoted to the spatiotemporal case. To fill this gap, we propose a scalable architecture that exploits an efficient encoding of both temporal and spatial dynamics. In particular, we use a randomized recurrent neural network to embed the history of the input time series into high-dimensional state representations encompassing multi-scale temporal dynamics. Such representations are then propagated along the spatial dimension using different powers of the graph adjacency matrix to generate node embeddings characterized by a rich pool of spatiotemporal features. The resulting node embeddings can be efficiently pre-computed in an unsupervised manner, before being fed to a feed-forward decoder that learns to map the multi-scale spatiotemporal representations to predictions. The training procedure can then be parallelized node-wise by sampling the node embeddings without breaking any dependency, thus enabling scalability to large networks. Empirical results on relevant datasets show that our approach achieves results competitive with the state of the art, while dramatically reducing the computational burden.

Learning to Reconstruct Missing Data from Spatiotemporal Graphs with Sparse Observations

Modeling multivariate time series as temporal signals over a (possibly dynamic) graph is an effective representational framework that allows for developing models for time series analysis. In fact, discrete sequences of graphs can be processed by autoregressive graph neural networks to recursively learn representations at each discrete point in time and space. Spatiotemporal graphs are often highly sparse, with time series characterized by multiple, concurrent, and even long sequences of missing data, e.g., due to the unreliable underlying sensor network. In this context, autoregressive models can be brittle and exhibit unstable learning dynamics. The objective of this paper is, then, to tackle the problem of learning effective models to reconstruct, i.e., impute, missing data points by conditioning the reconstruction only on the available observations. In particular, we propose a novel class of attention-based architectures that, given a set of highly sparse discrete observations, learn a representation for points in time and space by exploiting a spatiotemporal diffusion architecture aligned with the imputation task. Representations are trained end-to-end to reconstruct observations w.r.t. the corresponding sensor and its neighboring nodes. Compared to the state of the art, our model handles sparse data without propagating prediction errors or requiring a bidirectional model to encode forward and backward time dependencies. Empirical results on representative benchmarks show the effectiveness of the proposed method.

Multivariate Time Series Imputation by Graph Neural Networks

Dealing with missing values and incomplete time series is a labor-intensive and time-consuming inevitable task when handling data coming from real-world applications. Effective spatio-temporal representations would allow imputation methods to reconstruct missing temporal data by exploiting information coming from sensors at different locations. However, standard methods fall short in capturing the nonlinear time and space dependencies existing within networks of interconnected sensors and do not take full advantage of the available - and often strong - relational information. Notably, most of state-of-the-art imputation methods based on deep learning do not explicitly model relational aspects and, in any case, do not exploit processing frameworks able to adequately represent structured spatio-temporal data. Conversely, graph neural networks have recently surged in popularity as both expressive and scalable tools for processing sequential data with relational inductive biases. In this work, we present the first assessment of graph neural networks in the context of multivariate time series imputation. In particular, we introduce a novel graph neural network architecture, named GRIL, which aims at reconstructing missing data in the different channels of a multivariate time series by learning spatial-temporal representations through message passing. Preliminary empirical results show that our model outperforms state-of-the-art methods in the imputation task on relevant benchmarks with mean absolute error improvements often higher than 20%.