What Matters in Deep Learning for Time Series Forecasting?

Deep learning models have grown increasingly popular in time series applications. However, the large quantity of newly proposed architectures, together with often contradictory empirical results, makes it difficult to assess which components contribute significantly to final performance. We aim to make sense of the current design space of deep learning architectures for time series forecasting by discussing the design dimensions and trade-offs that can explain, often unexpected, observed results. This paper discusses the necessity of grounding model design on principles for forecasting groups of time series and how such principles can be applied to current models. In particular, we assess how concepts such as locality and globality apply to recent forecasting architectures. We show that accounting for these aspects can be more relevant for achieving accurate results than adopting specific sequence modeling layers and that simple, well-designed forecasting architectures can often match the state of the art. We discuss how overlooked implementation details in existing architectures (1) fundamentally change the class of the resulting forecasting method and (2) drastically affect the observed empirical results. Our results call for rethinking current faulty benchmarking practices and the need to focus on the foundational aspects of the forecasting problem when designing architectures. As a step in this direction, we propose an auxiliary forecasting model card, whose fields serve to characterize existing and new forecasting architectures based on key design choices.

ResCP: Reservoir Conformal Prediction for Time Series Forecasting

Conformal prediction offers a powerful framework for building distribution-free prediction intervals for exchangeable data. Existing methods that extend conformal prediction to sequential data rely on fitting a relatively complex model to capture temporal dependencies. However, these methods can fail if the sample size is small and often require expensive retraining when the underlying data distribution changes. To overcome these limitations, we propose Reservoir Conformal Prediction (ResCP), a novel training-free conformal prediction method for time series. Our approach leverages the efficiency and representation learning capabilities of reservoir computing to dynamically reweight conformity scores. In particular, we compute similarity scores among reservoir states and use them to adaptively reweight the observed residuals at each step. With this approach, ResCP enables us to account for local temporal dynamics when modeling the error distribution without compromising computational scalability. We prove that, under reasonable assumptions, ResCP achieves asymptotic conditional coverage, and we empirically demonstrate its effectiveness across diverse forecasting tasks.

Hierarchical Message-Passing Policies for Multi-Agent Reinforcement Learning

Decentralized Multi-Agent Reinforcement Learning (MARL) methods allow for learning scalable multi-agent policies, but suffer from partial observability and induced non-stationarity. These challenges can be addressed by introducing mechanisms that facilitate coordination and high-level planning. Specifically, coordination and temporal abstraction can be achieved through communication (e.g., message passing) and Hierarchical Reinforcement Learning (HRL) approaches to decision-making. However, optimization issues limit the applicability of hierarchical policies to multi-agent systems. As such, the combination of these approaches has not been fully explored. To fill this void, we propose a novel and effective methodology for learning multi-agent hierarchies of message-passing policies. We adopt the feudal HRL framework and rely on a hierarchical graph structure for planning and coordination among agents. Agents at lower levels in the hierarchy receive goals from the upper levels and exchange messages with neighboring agents at the same level. To learn hierarchical multi-agent policies, we design a novel reward-assignment method based on training the lower-level policies to maximize the advantage function associated with the upper levels. Results on relevant benchmarks show that our method performs favorably compared to the state of the art.

Deep Reinforcement Learning Policies for Underactuated Satellite Attitude Control

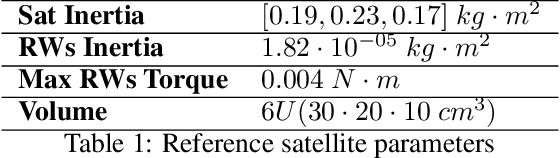
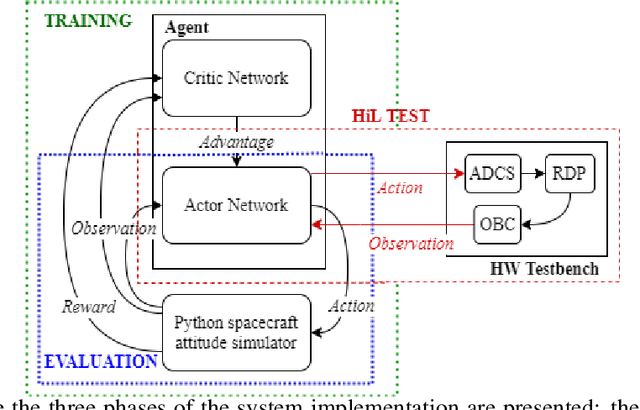
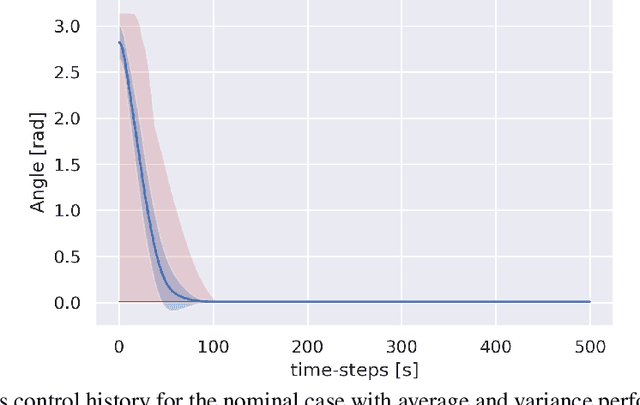
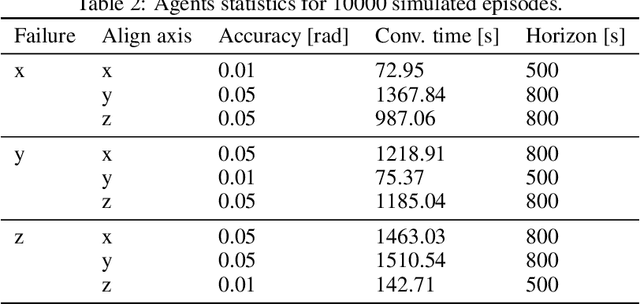
Autonomy is a key challenge for future space exploration endeavours. Deep Reinforcement Learning holds the promises for developing agents able to learn complex behaviours simply by interacting with their environment. This paper investigates the use of Reinforcement Learning for the satellite attitude control problem, namely the angular reorientation of a spacecraft with respect to an in- ertial frame of reference. In the proposed approach, a set of control policies are implemented as neural networks trained with a custom version of the Proximal Policy Optimization algorithm to maneuver a small satellite from a random starting angle to a given pointing target. In particular, we address the problem for two working conditions: the nominal case, in which all the actuators (a set of 3 reac- tion wheels) are working properly, and the underactuated case, where an actuator failure is simulated randomly along with one of the axes. We show that the agents learn to effectively perform large-angle slew maneuvers with fast convergence and industry-standard pointing accuracy. Furthermore, we test the proposed method on representative hardware, showing that by taking adequate measures controllers trained in simulation can perform well in real systems.

Relational Conformal Prediction for Correlated Time Series

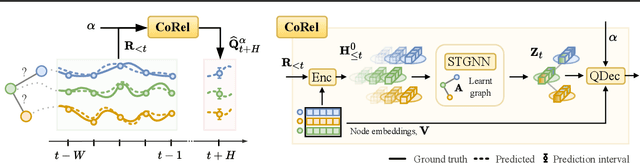
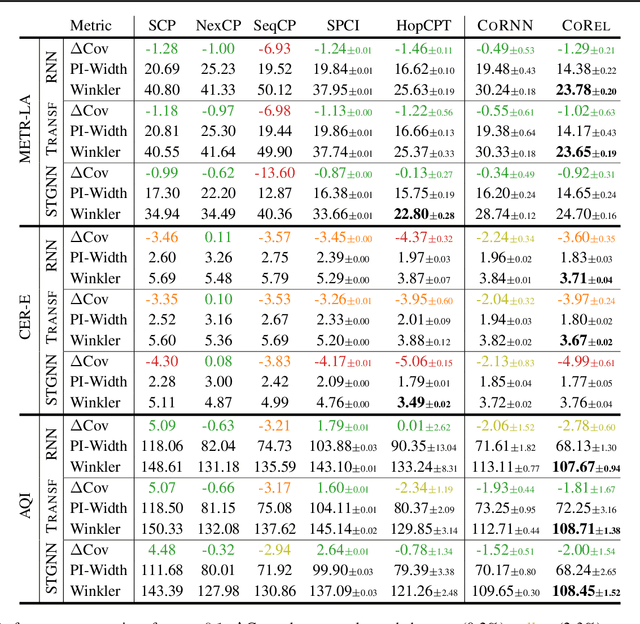
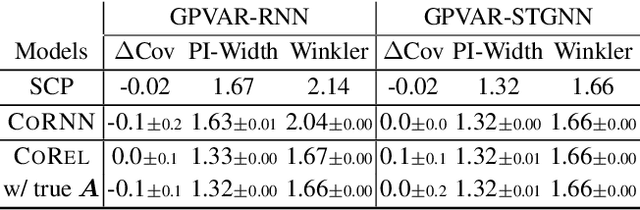
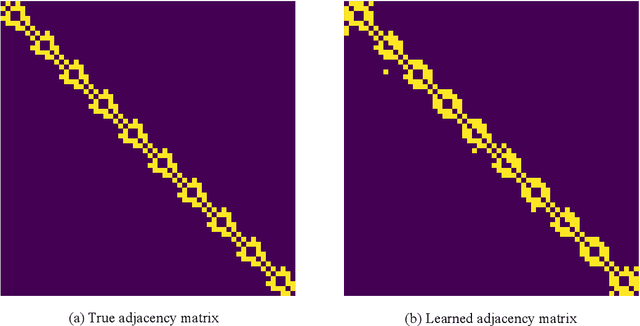
We address the problem of uncertainty quantification in time series forecasting by exploiting observations at correlated sequences. Relational deep learning methods leveraging graph representations are among the most effective tools for obtaining point estimates from spatiotemporal data and correlated time series. However, the problem of exploiting relational structures to estimate the uncertainty of such predictions has been largely overlooked in the same context. To this end, we propose a novel distribution-free approach based on the conformal prediction framework and quantile regression. Despite the recent applications of conformal prediction to sequential data, existing methods operate independently on each target time series and do not account for relationships among them when constructing the prediction interval. We fill this void by introducing a novel conformal prediction method based on graph deep learning operators. Our method, named Conformal Relational Prediction (CoRel), does not require the relational structure (graph) to be known as a prior and can be applied on top of any pre-trained time series predictor. Additionally, CoRel includes an adaptive component to handle non-exchangeable data and changes in the input time series. Our approach provides accurate coverage and archives state-of-the-art uncertainty quantification in relevant benchmarks.

Learning to Predict Global Atrial Fibrillation Dynamics from Sparse Measurements

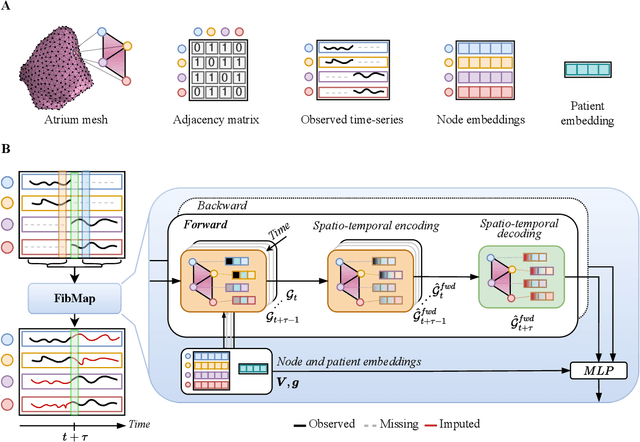
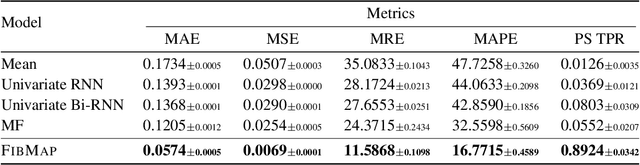
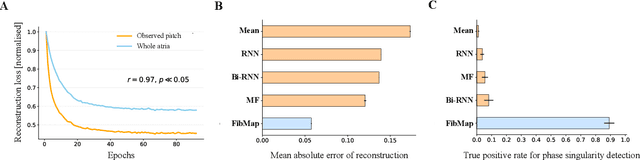
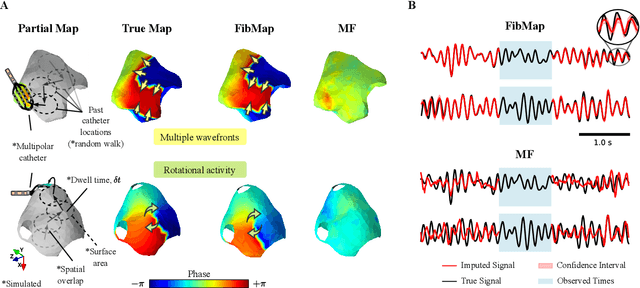
Catheter ablation of Atrial Fibrillation (AF) consists of a one-size-fits-all treatment with limited success in persistent AF. This may be due to our inability to map the dynamics of AF with the limited resolution and coverage provided by sequential contact mapping catheters, preventing effective patient phenotyping for personalised, targeted ablation. Here we introduce FibMap, a graph recurrent neural network model that reconstructs global AF dynamics from sparse measurements. Trained and validated on 51 non-contact whole atria recordings, FibMap reconstructs whole atria dynamics from 10% surface coverage, achieving a 210% lower mean absolute error and an order of magnitude higher performance in tracking phase singularities compared to baseline methods. Clinical utility of FibMap is demonstrated on real-world contact mapping recordings, achieving reconstruction fidelity comparable to non-contact mapping. FibMap's state-spaces and patient-specific parameters offer insights for electrophenotyping AF. Integrating FibMap into clinical practice could enable personalised AF care and improve outcomes.

On the Regularization of Learnable Embeddings for Time Series Processing

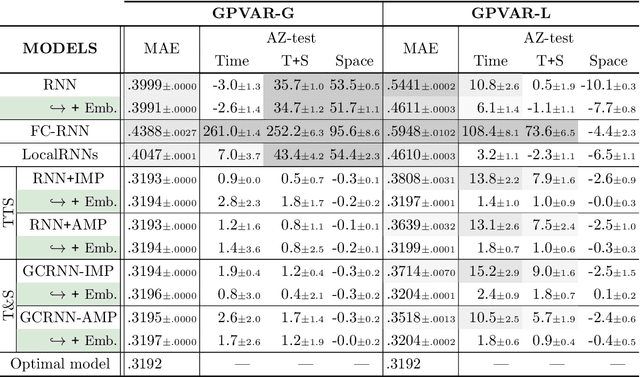
In processing multiple time series, accounting for the individual features of each sequence can be challenging. To address this, modern deep learning methods for time series analysis combine a shared (global) model with local layers, specific to each time series, often implemented as learnable embeddings. Ideally, these local embeddings should encode meaningful representations of the unique dynamics of each sequence. However, when these are learned end-to-end as parameters of a forecasting model, they may end up acting as mere sequence identifiers. Shared processing blocks may then become reliant on such identifiers, limiting their transferability to new contexts. In this paper, we address this issue by investigating methods to regularize the learning of local learnable embeddings for time series processing. Specifically, we perform the first extensive empirical study on the subject and show how such regularizations consistently improve performance in widely adopted architectures. Furthermore, we show that methods preventing the co-adaptation of local and global parameters are particularly effective in this context. This hypothesis is validated by comparing several methods preventing the downstream models from relying on sequence identifiers, going as far as completely resetting the embeddings during training. The obtained results provide an important contribution to understanding the interplay between learnable local parameters and shared processing layers: a key challenge in modern time series processing models and a step toward developing effective foundation models for time series.

Graph-based Virtual Sensing from Sparse and Partial Multivariate Observations

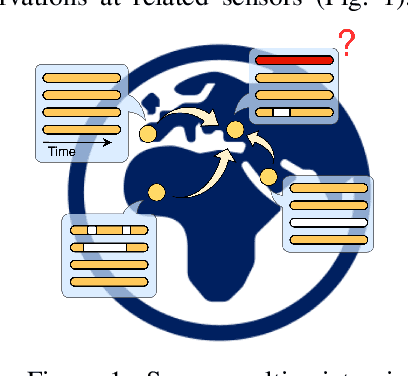
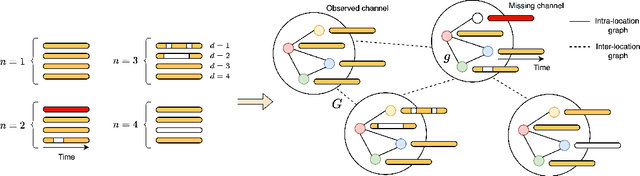
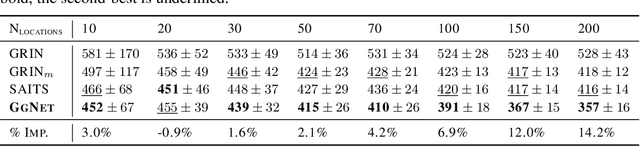
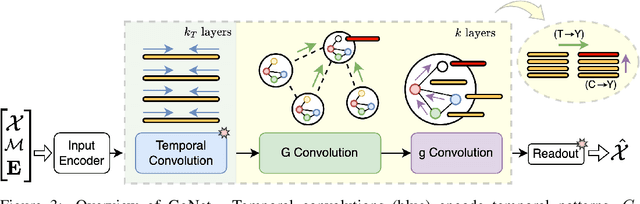
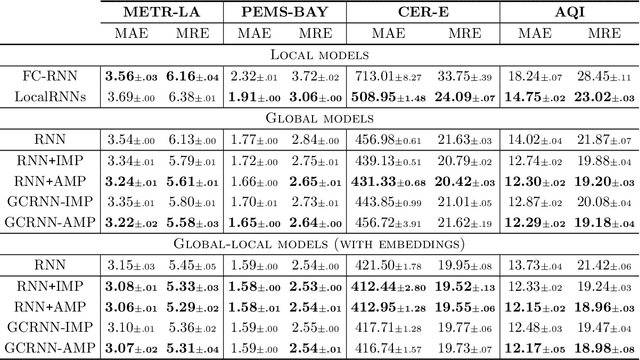
Virtual sensing techniques allow for inferring signals at new unmonitored locations by exploiting spatio-temporal measurements coming from physical sensors at different locations. However, as the sensor coverage becomes sparse due to costs or other constraints, physical proximity cannot be used to support interpolation. In this paper, we overcome this challenge by leveraging dependencies between the target variable and a set of correlated variables (covariates) that can frequently be associated with each location of interest. From this viewpoint, covariates provide partial observability, and the problem consists of inferring values for unobserved channels by exploiting observations at other locations to learn how such variables can correlate. We introduce a novel graph-based methodology to exploit such relationships and design a graph deep learning architecture, named GgNet, implementing the framework. The proposed approach relies on propagating information over a nested graph structure that is used to learn dependencies between variables as well as locations. GgNet is extensively evaluated under different virtual sensing scenarios, demonstrating higher reconstruction accuracy compared to the state-of-the-art.

Graph Deep Learning for Time Series Forecasting

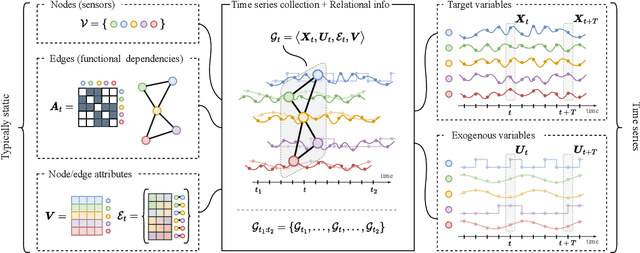
Graph-based deep learning methods have become popular tools to process collections of correlated time series. Differently from traditional multivariate forecasting methods, neural graph-based predictors take advantage of pairwise relationships by conditioning forecasts on a (possibly dynamic) graph spanning the time series collection. The conditioning can take the form of an architectural inductive bias on the neural forecasting architecture, resulting in a family of deep learning models called spatiotemporal graph neural networks. Such relational inductive biases enable the training of global forecasting models on large time-series collections, while at the same time localizing predictions w.r.t. each element in the set (i.e., graph nodes) by accounting for local correlations among them (i.e., graph edges). Indeed, recent theoretical and practical advances in graph neural networks and deep learning for time series forecasting make the adoption of such processing frameworks appealing and timely. However, most of the studies in the literature focus on proposing variations of existing neural architectures by taking advantage of modern deep learning practices, while foundational and methodological aspects have not been subject to systematic investigation. To fill the gap, this paper aims to introduce a comprehensive methodological framework that formalizes the forecasting problem and provides design principles for graph-based predictive models and methods to assess their performance. At the same time, together with an overview of the field, we provide design guidelines, recommendations, and best practices, as well as an in-depth discussion of open challenges and future research directions.

Graph-based Time Series Clustering for End-to-End Hierarchical Forecasting

Existing relationships among time series can be exploited as inductive biases in learning effective forecasting models. In hierarchical time series, relationships among subsets of sequences induce hard constraints (hierarchical inductive biases) on the predicted values. In this paper, we propose a graph-based methodology to unify relational and hierarchical inductive biases in the context of deep learning for time series forecasting. In particular, we model both types of relationships as dependencies in a pyramidal graph structure, with each pyramidal layer corresponding to a level of the hierarchy. By exploiting modern - trainable - graph pooling operators we show that the hierarchical structure, if not available as a prior, can be learned directly from data, thus obtaining cluster assignments aligned with the forecasting objective. A differentiable reconciliation stage is incorporated into the processing architecture, allowing hierarchical constraints to act both as an architectural bias as well as a regularization element for predictions. Simulation results on representative datasets show that the proposed method compares favorably against the state of the art.