Promptable Foundation Models for SAR Remote Sensing: Adapting the Segment Anything Model for Snow Avalanche Segmentation

Remote sensing solutions for avalanche segmentation and mapping are key to supporting risk forecasting and mitigation in mountain regions. Synthetic Aperture Radar (SAR) imagery from Sentinel-1 can be effectively used for this task, but training an effective detection model requires gathering a large dataset with high-quality annotations from domain experts, which is prohibitively time-consuming. In this work, we aim to facilitate and accelerate the annotation of SAR images for avalanche mapping. We build on the Segment Anything Model (SAM), a segmentation foundation model trained on natural images, and tailor it to Sentinel-1 SAR data. Adapting SAM to our use-case requires addressing several domain-specific challenges: (i) domain mismatch, since SAM was not trained on satellite/SAR imagery; (ii) input adaptation, because SAR products typically provide more than three channels, while SAM is constrained to RGB images; (iii) robustness to imprecise prompts that can affect target identification and degrade the segmentation quality, an issue exacerbated in small, low-contrast avalanches; and (iv) training efficiency, since standard fine-tuning is computationally demanding for SAM. We tackle these challenges through a combination of adapters to mitigate the domain gap, multiple encoders to handle multi-channel SAR inputs, prompt-engineering strategies to improve avalanche localization accuracy, and a training algorithm that limits the training time of the encoder, which is recognized as the major bottleneck. We integrate the resulting model into an annotation tool and show experimentally that it speeds up the annotation of SAR images.

Torch Geometric Pool: the Pytorch library for pooling in Graph Neural Networks

We introduce Torch Geometric Pool (tgp), a library for hierarchical pooling in Graph Neural Networks. Built upon Pytorch Geometric, Torch Geometric Pool (tgp) provides a wide variety of pooling operators, unified under a consistent API and a modular design. The library emphasizes usability and extensibility, and includes features like precomputed pooling, which significantly accelerate training for a class of operators. In this paper, we present tgp's structure and present an extensive benchmark. The latter showcases the library's features and systematically compares the performance of the implemented graph-pooling methods in different downstream tasks. The results, showing that the choice of the optimal pooling operator depends on tasks and data at hand, support the need for a library that enables fast prototyping.

ResCP: Reservoir Conformal Prediction for Time Series Forecasting

Conformal prediction offers a powerful framework for building distribution-free prediction intervals for exchangeable data. Existing methods that extend conformal prediction to sequential data rely on fitting a relatively complex model to capture temporal dependencies. However, these methods can fail if the sample size is small and often require expensive retraining when the underlying data distribution changes. To overcome these limitations, we propose Reservoir Conformal Prediction (ResCP), a novel training-free conformal prediction method for time series. Our approach leverages the efficiency and representation learning capabilities of reservoir computing to dynamically reweight conformity scores. In particular, we compute similarity scores among reservoir states and use them to adaptively reweight the observed residuals at each step. With this approach, ResCP enables us to account for local temporal dynamics when modeling the error distribution without compromising computational scalability. We prove that, under reasonable assumptions, ResCP achieves asymptotic conditional coverage, and we empirically demonstrate its effectiveness across diverse forecasting tasks.

Monitoring snow avalanches from SAR data with deep learning

Snow avalanches present significant risks to human life and infrastructure, particularly in mountainous regions, making effective monitoring crucial. Traditional monitoring methods, such as field observations, are limited by accessibility, weather conditions, and cost. Satellite-borne Synthetic Aperture Radar (SAR) data has become an important tool for large-scale avalanche detection, as it can capture data in all weather conditions and across remote areas. However, traditional processing methods struggle with the complexity and variability of avalanches. This chapter reviews the application of deep learning for detecting and segmenting snow avalanches from SAR data. Early efforts focused on the binary classification of SAR images, while recent advances have enabled pixel-level segmentation, providing greater accuracy and spatial resolution. A case study using Sentinel-1 SAR data demonstrates the effectiveness of deep learning models for avalanche segmentation, achieving superior results over traditional methods. We also present an extension of this work, testing recent state-of-the-art segmentation architectures on an expanded dataset of over 4,500 annotated SAR images. The best-performing model among those tested was applied for large-scale avalanche detection across the whole of Norway, revealing important spatial and temporal patterns over several winter seasons.

Relational Conformal Prediction for Correlated Time Series

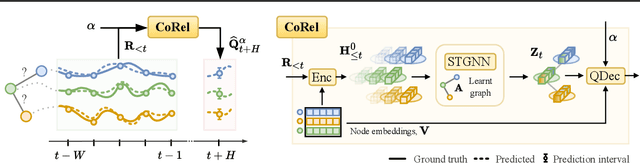
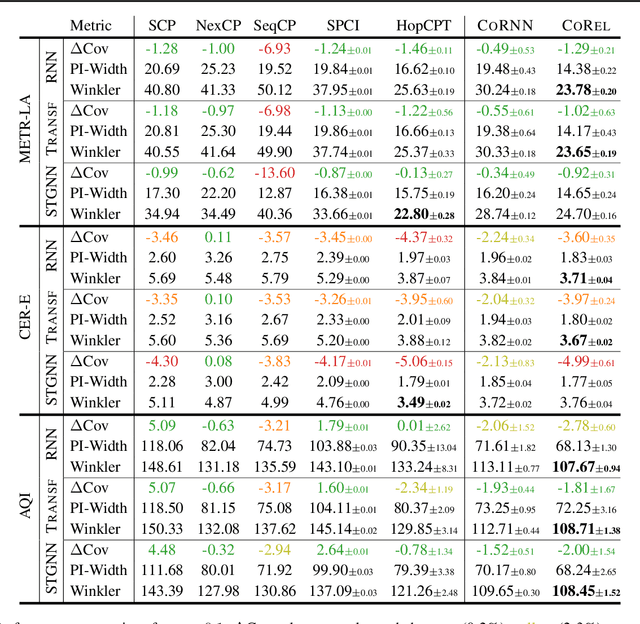
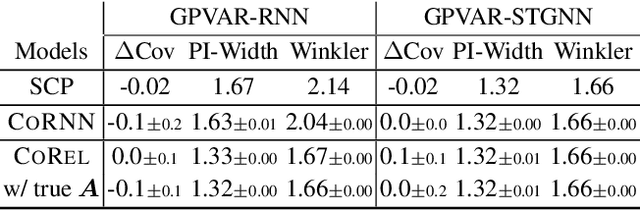
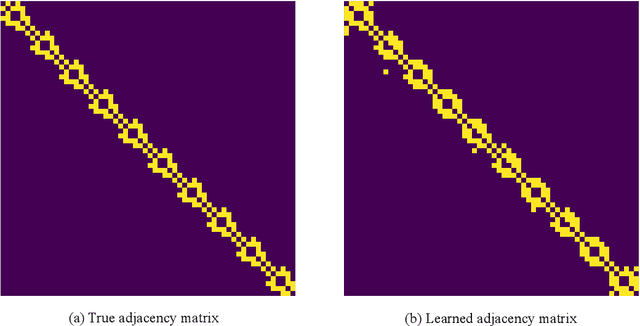
We address the problem of uncertainty quantification in time series forecasting by exploiting observations at correlated sequences. Relational deep learning methods leveraging graph representations are among the most effective tools for obtaining point estimates from spatiotemporal data and correlated time series. However, the problem of exploiting relational structures to estimate the uncertainty of such predictions has been largely overlooked in the same context. To this end, we propose a novel distribution-free approach based on the conformal prediction framework and quantile regression. Despite the recent applications of conformal prediction to sequential data, existing methods operate independently on each target time series and do not account for relationships among them when constructing the prediction interval. We fill this void by introducing a novel conformal prediction method based on graph deep learning operators. Our method, named Conformal Relational Prediction (CoRel), does not require the relational structure (graph) to be known as a prior and can be applied on top of any pre-trained time series predictor. Additionally, CoRel includes an adaptive component to handle non-exchangeable data and changes in the input time series. Our approach provides accurate coverage and archives state-of-the-art uncertainty quantification in relevant benchmarks.

Interpreting Temporal Graph Neural Networks with Koopman Theory

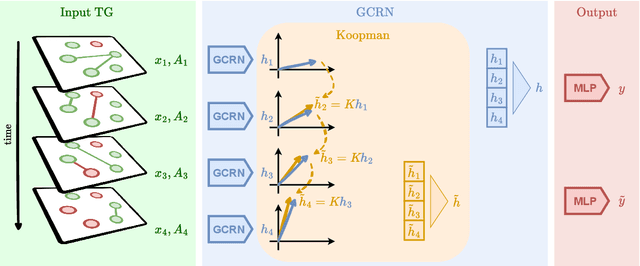
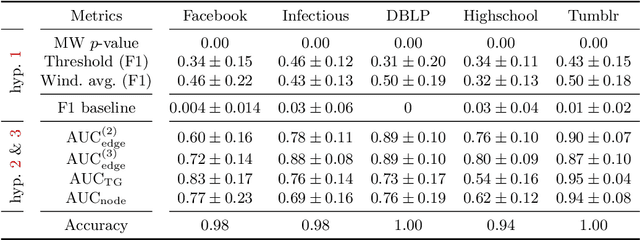
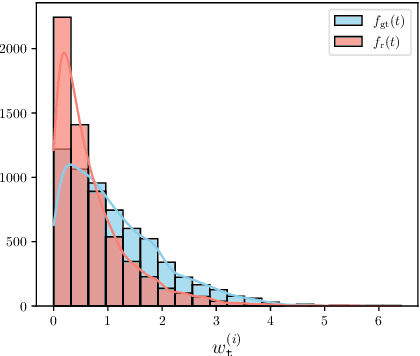
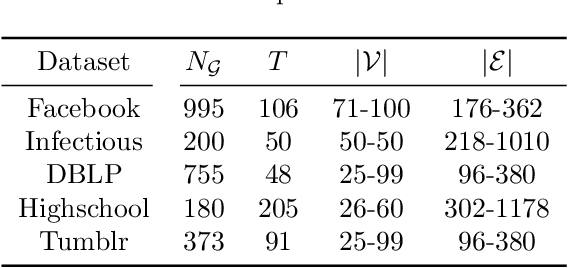
Spatiotemporal graph neural networks (STGNNs) have shown promising results in many domains, from forecasting to epidemiology. However, understanding the dynamics learned by these models and explaining their behaviour is significantly more complex than for models dealing with static data. Inspired by Koopman theory, which allows a simpler description of intricate, nonlinear dynamical systems, we introduce an explainability approach for temporal graphs. We present two methods to interpret the STGNN's decision process and identify the most relevant spatial and temporal patterns in the input for the task at hand. The first relies on dynamic mode decomposition (DMD), a Koopman-inspired dimensionality reduction method. The second relies on sparse identification of nonlinear dynamics (SINDy), a popular method for discovering governing equations, which we use for the first time as a general tool for explainability. We show how our methods can correctly identify interpretable features such as infection times and infected nodes in the context of dissemination processes.

MaxCutPool: differentiable feature-aware Maxcut for pooling in graph neural networks

We propose a novel approach to compute the MAXCUT in attributed graphs, i.e., graphs with features associated with nodes and edges. Our approach is robust to the underlying graph topology and is fully differentiable, making it possible to find solutions that jointly optimize the MAXCUT along with other objectives. Based on the obtained MAXCUT partition, we implement a hierarchical graph pooling layer for Graph Neural Networks, which is sparse, differentiable, and particularly suitable for downstream tasks on heterophilic graphs.

Graph-based Forecasting with Missing Data through Spatiotemporal Downsampling

Given a set of synchronous time series, each associated with a sensor-point in space and characterized by inter-series relationships, the problem of spatiotemporal forecasting consists of predicting future observations for each point. Spatiotemporal graph neural networks achieve striking results by representing the relationships across time series as a graph. Nonetheless, most existing methods rely on the often unrealistic assumption that inputs are always available and fail to capture hidden spatiotemporal dynamics when part of the data is missing. In this work, we tackle this problem through hierarchical spatiotemporal downsampling. The input time series are progressively coarsened over time and space, obtaining a pool of representations that capture heterogeneous temporal and spatial dynamics. Conditioned on observations and missing data patterns, such representations are combined by an interpretable attention mechanism to generate the forecasts. Our approach outperforms state-of-the-art methods on synthetic and real-world benchmarks under different missing data distributions, particularly in the presence of contiguous blocks of missing values.

Probabilistic load forecasting with Reservoir Computing

Some applications of deep learning require not only to provide accurate results but also to quantify the amount of confidence in their prediction. The management of an electric power grid is one of these cases: to avoid risky scenarios, decision-makers need both precise and reliable forecasts of, for example, power loads. For this reason, point forecasts are not enough hence it is necessary to adopt methods that provide an uncertainty quantification. This work focuses on reservoir computing as the core time series forecasting method, due to its computational efficiency and effectiveness in predicting time series. While the RC literature mostly focused on point forecasting, this work explores the compatibility of some popular uncertainty quantification methods with the reservoir setting. Both Bayesian and deterministic approaches to uncertainty assessment are evaluated and compared in terms of their prediction accuracy, computational resource efficiency and reliability of the estimated uncertainty, based on a set of carefully chosen performance metrics.

The expressive power of pooling in Graph Neural Networks

In Graph Neural Networks (GNNs), hierarchical pooling operators generate local summaries of the data by coarsening the graph structure and the vertex features. Considerable attention has been devoted to analyzing the expressive power of message-passing (MP) layers in GNNs, while a study on how graph pooling affects the expressiveness of a GNN is still lacking. Additionally, despite the recent advances in the design of pooling operators, there is not a principled criterion to compare them. In this work, we derive sufficient conditions for a pooling operator to fully preserve the expressive power of the MP layers before it. These conditions serve as a universal and theoretically-grounded criterion for choosing among existing pooling operators or designing new ones. Based on our theoretical findings, we analyze several existing pooling operators and identify those that fail to satisfy the expressiveness conditions. Finally, we introduce an experimental setup to verify empirically the expressive power of a GNN equipped with pooling layers, in terms of its capability to perform a graph isomorphism test.