Hyperbolic Graph Neural Networks Under the Microscope: The Role of Geometry-Task Alignment

Many complex networks exhibit hyperbolic structural properties, making hyperbolic space a natural candidate for representing hierarchical and tree-like graphs with low distortion. Based on this observation, Hyperbolic Graph Neural Networks (HGNNs) have been widely adopted as a principled choice for representation learning on tree-like graphs. In this work, we question this paradigm by proposing an additional condition of geometry-task alignment, i.e., whether the metric structure of the target follows that of the input graph. We theoretically and empirically demonstrate the capability of HGNNs to recover low-distortion representations on two synthetic regression problems, and show that their geometric inductive bias becomes helpful when the problem requires preserving metric structure. Additionally, we evaluate HGNNs on the tasks of link prediction and node classification by jointly analyzing predictive performance and embedding distortion, revealing that only link prediction is geometry-aligned. Overall, our findings shift the focus from only asking "Is the graph hyperbolic?" to also questioning "Is the task aligned with hyperbolic geometry?", showing that HGNNs consistently outperform Euclidean models under such alignment, while their advantage vanishes otherwise.

Rethinking GNNs and Missing Features: Challenges, Evaluation and a Robust Solution

Handling missing node features is a key challenge for deploying Graph Neural Networks (GNNs) in real-world domains such as healthcare and sensor networks. Existing studies mostly address relatively benign scenarios, namely benchmark datasets with (a) high-dimensional but sparse node features and (b) incomplete data generated under Missing Completely At Random (MCAR) mechanisms. For (a), we theoretically prove that high sparsity substantially limits the information loss caused by missingness, making all models appear robust and preventing a meaningful comparison of their performance. To overcome this limitation, we introduce one synthetic and three real-world datasets with dense, semantically meaningful features. For (b), we move beyond MCAR and design evaluation protocols with more realistic missingness mechanisms. Moreover, we provide a theoretical background to state explicit assumptions on the missingness process and analyze their implications for different methods. Building on this analysis, we propose GNNmim, a simple yet effective baseline for node classification with incomplete feature data. Experiments show that GNNmim is competitive with respect to specialized architectures across diverse datasets and missingness regimes.

Boosting Relational Deep Learning with Pretrained Tabular Models

Relational databases, organized into tables connected by primary-foreign key relationships, are a common format for organizing data. Making predictions on relational data often involves transforming them into a flat tabular format through table joins and feature engineering, which serve as input to tabular methods. However, designing features that fully capture complex relational patterns remains challenging. Graph Neural Networks (GNNs) offer a compelling alternative by inherently modeling these relationships, but their time overhead during inference limits their applicability for real-time scenarios. In this work, we aim to bridge this gap by leveraging existing feature engineering efforts to enhance the efficiency of GNNs in relational databases. Specifically, we use GNNs to capture complex relationships within relational databases, patterns that are difficult to featurize, while employing engineered features to encode temporal information, thereby avoiding the need to retain the entire historical graph and enabling the use of smaller, more efficient graphs. Our \textsc{LightRDL} approach not only improves efficiency, but also outperforms existing models. Experimental results on the RelBench benchmark demonstrate that our framework achieves up to $33\%$ performance improvement and a $526\times$ inference speedup compared to GNNs, making it highly suitable for real-time inference.

The expressive power of pooling in Graph Neural Networks

In Graph Neural Networks (GNNs), hierarchical pooling operators generate local summaries of the data by coarsening the graph structure and the vertex features. Considerable attention has been devoted to analyzing the expressive power of message-passing (MP) layers in GNNs, while a study on how graph pooling affects the expressiveness of a GNN is still lacking. Additionally, despite the recent advances in the design of pooling operators, there is not a principled criterion to compare them. In this work, we derive sufficient conditions for a pooling operator to fully preserve the expressive power of the MP layers before it. These conditions serve as a universal and theoretically-grounded criterion for choosing among existing pooling operators or designing new ones. Based on our theoretical findings, we analyze several existing pooling operators and identify those that fail to satisfy the expressiveness conditions. Finally, we introduce an experimental setup to verify empirically the expressive power of a GNN equipped with pooling layers, in terms of its capability to perform a graph isomorphism test.

Graph Neural Networks for temporal graphs: State of the art, open challenges, and opportunities

Graph Neural Networks (GNNs) have become the leading paradigm for learning on (static) graph-structured data. However, many real-world systems are dynamic in nature, since the graph and node/edge attributes change over time. In recent years, GNN-based models for temporal graphs have emerged as a promising area of research to extend the capabilities of GNNs. In this work, we provide the first comprehensive overview of the current state-of-the-art of temporal GNN, introducing a rigorous formalization of learning settings and tasks and a novel taxonomy categorizing existing approaches in terms of how the temporal aspect is represented and processed. We conclude the survey with a discussion of the most relevant open challenges for the field, from both research and application perspectives.

Weisfeiler--Lehman goes Dynamic: An Analysis of the Expressive Power of Graph Neural Networks for Attributed and Dynamic Graphs

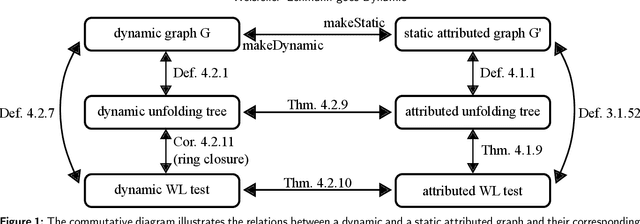
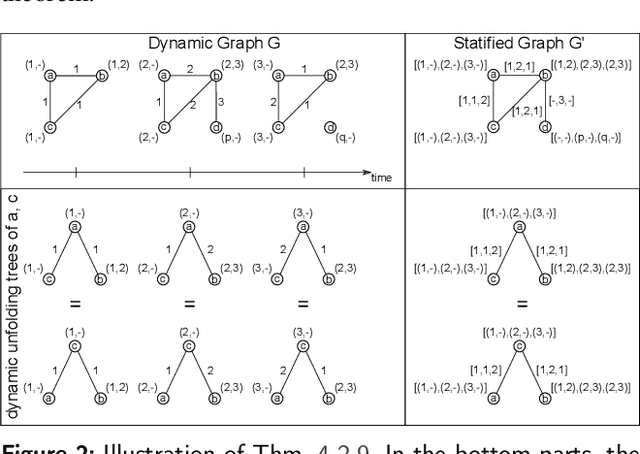
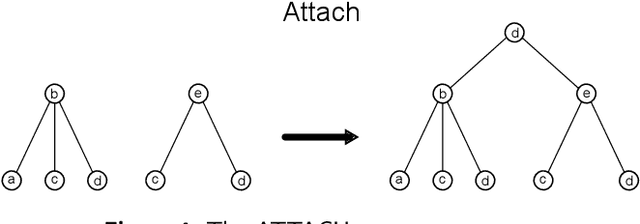
Graph Neural Networks (GNNs) are a large class of relational models for graph processing. Recent theoretical studies on the expressive power of GNNs have focused on two issues. On the one hand, it has been proven that GNNs are as powerful as the Weisfeiler-Lehman test (1-WL) in their ability to distinguish graphs. Moreover, it has been shown that the equivalence enforced by 1-WL equals unfolding equivalence. On the other hand, GNNs turned out to be universal approximators on graphs modulo the constraints enforced by 1-WL/unfolding equivalence. However, these results only apply to Static Undirected Homogeneous Graphs with node attributes. In contrast, real-life applications often involve a variety of graph properties, such as, e.g., dynamics or node and edge attributes. In this paper, we conduct a theoretical analysis of the expressive power of GNNs for these two graph types that are particularly of interest. Dynamic graphs are widely used in modern applications, and its theoretical analysis requires new approaches. The attributed type acts as a standard form for all graph types since it has been shown that all graph types can be transformed without loss to Static Undirected Homogeneous Graphs with attributes on nodes and edges (SAUHG). The study considers generic GNN models and proposes appropriate 1-WL tests for those domains. Then, the results on the expressive power of GNNs are extended by proving that GNNs have the same capability as the 1-WL test in distinguishing dynamic and attributed graphs, the 1-WL equivalence equals unfolding equivalence and that GNNs are universal approximators modulo 1-WL/unfolding equivalence. Moreover, the proof of the approximation capability holds for SAUHGs, which include most of those used in practical applications, and it is constructive in nature allowing to deduce hints on the architecture of GNNs that can achieve the desired accuracy.