Weisfeiler--Lehman goes Dynamic: An Analysis of the Expressive Power of Graph Neural Networks for Attributed and Dynamic Graphs

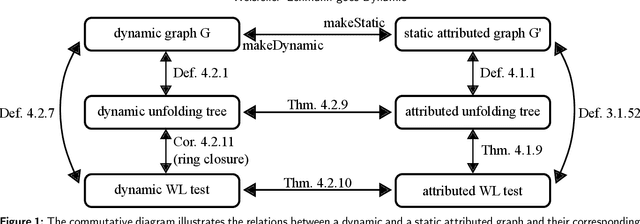
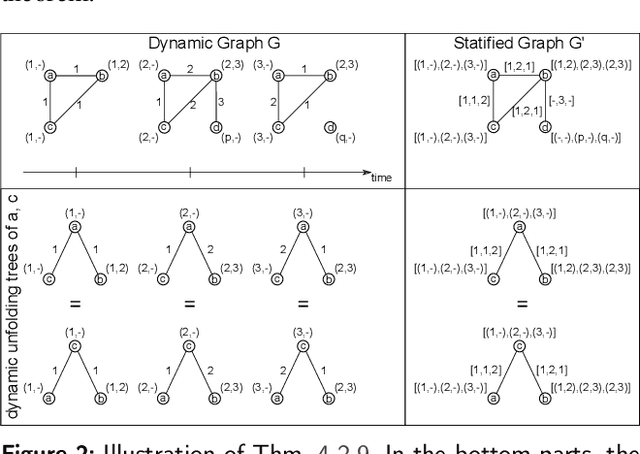
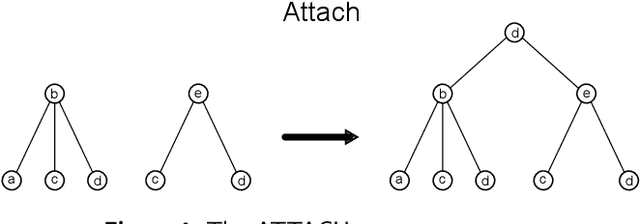
Graph Neural Networks (GNNs) are a large class of relational models for graph processing. Recent theoretical studies on the expressive power of GNNs have focused on two issues. On the one hand, it has been proven that GNNs are as powerful as the Weisfeiler-Lehman test (1-WL) in their ability to distinguish graphs. Moreover, it has been shown that the equivalence enforced by 1-WL equals unfolding equivalence. On the other hand, GNNs turned out to be universal approximators on graphs modulo the constraints enforced by 1-WL/unfolding equivalence. However, these results only apply to Static Undirected Homogeneous Graphs with node attributes. In contrast, real-life applications often involve a variety of graph properties, such as, e.g., dynamics or node and edge attributes. In this paper, we conduct a theoretical analysis of the expressive power of GNNs for these two graph types that are particularly of interest. Dynamic graphs are widely used in modern applications, and its theoretical analysis requires new approaches. The attributed type acts as a standard form for all graph types since it has been shown that all graph types can be transformed without loss to Static Undirected Homogeneous Graphs with attributes on nodes and edges (SAUHG). The study considers generic GNN models and proposes appropriate 1-WL tests for those domains. Then, the results on the expressive power of GNNs are extended by proving that GNNs have the same capability as the 1-WL test in distinguishing dynamic and attributed graphs, the 1-WL equivalence equals unfolding equivalence and that GNNs are universal approximators modulo 1-WL/unfolding equivalence. Moreover, the proof of the approximation capability holds for SAUHGs, which include most of those used in practical applications, and it is constructive in nature allowing to deduce hints on the architecture of GNNs that can achieve the desired accuracy.

Machine learning meets network science: dimensionality reduction for fast and efficient embedding of networks in the hyperbolic space

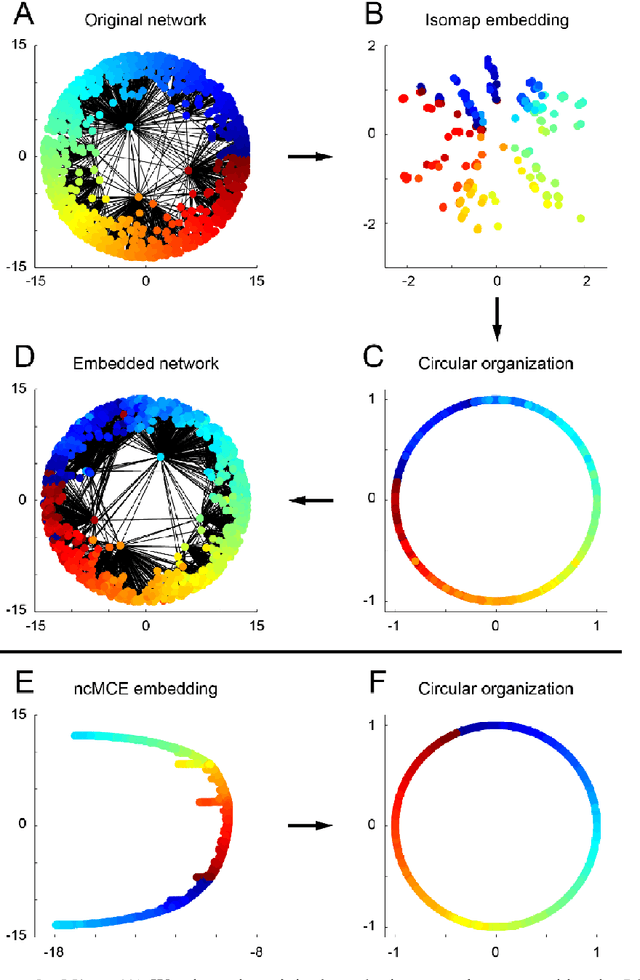
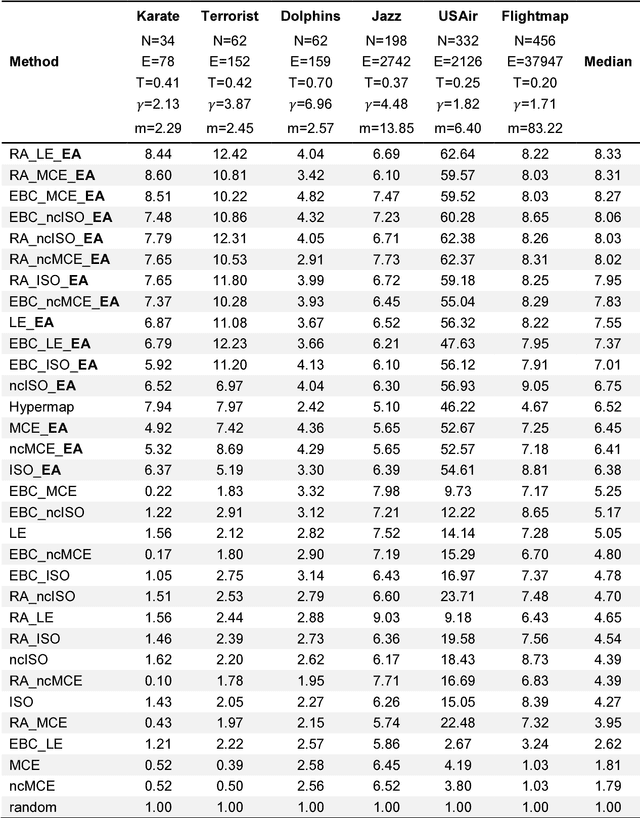
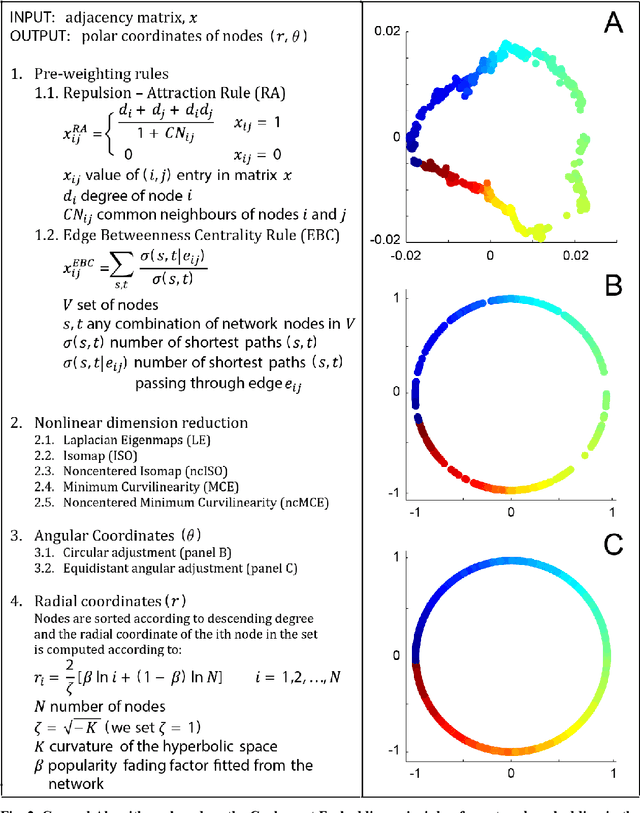
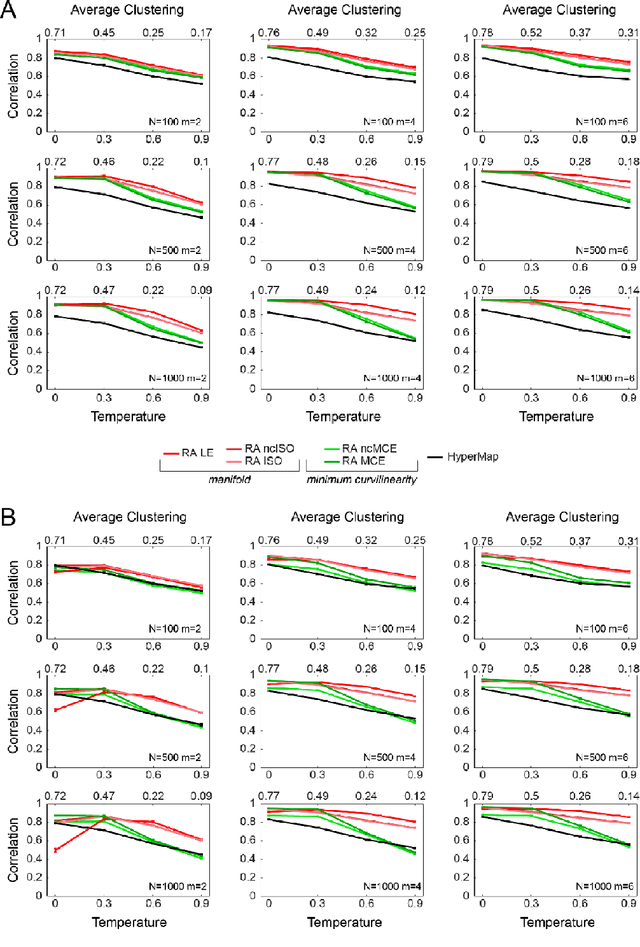
Complex network topologies and hyperbolic geometry seem specularly connected, and one of the most fascinating and challenging problems of recent complex network theory is to map a given network to its hyperbolic space. The Popularity Similarity Optimization (PSO) model represents - at the moment - the climax of this theory. It suggests that the trade-off between node popularity and similarity is a mechanism to explain how complex network topologies emerge - as discrete samples - from the continuous world of hyperbolic geometry. The hyperbolic space seems appropriate to represent real complex networks. In fact, it preserves many of their fundamental topological properties, and can be exploited for real applications such as, among others, link prediction and community detection. Here, we observe for the first time that a topological-based machine learning class of algorithms - for nonlinear unsupervised dimensionality reduction - can directly approximate the network's node angular coordinates of the hyperbolic model into a two-dimensional space, according to a similar topological organization that we named angular coalescence. On the basis of this phenomenon, we propose a new class of algorithms that offers fast and accurate coalescent embedding of networks in the hyperbolic space even for graphs with thousands of nodes.