Weisfeiler--Lehman goes Dynamic: An Analysis of the Expressive Power of Graph Neural Networks for Attributed and Dynamic Graphs

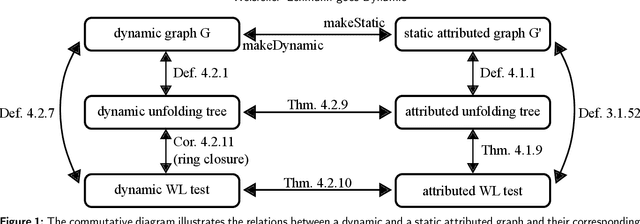
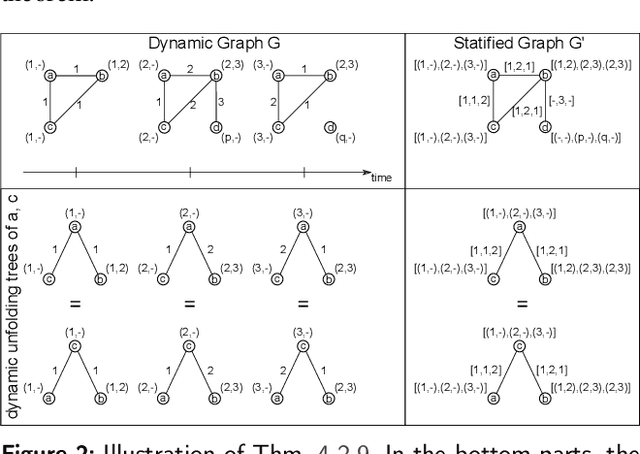
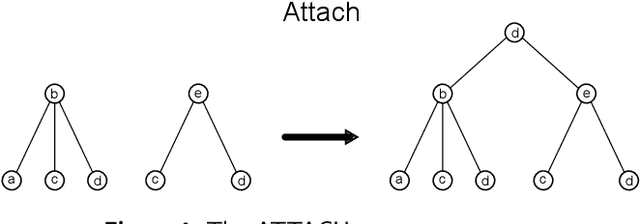
Graph Neural Networks (GNNs) are a large class of relational models for graph processing. Recent theoretical studies on the expressive power of GNNs have focused on two issues. On the one hand, it has been proven that GNNs are as powerful as the Weisfeiler-Lehman test (1-WL) in their ability to distinguish graphs. Moreover, it has been shown that the equivalence enforced by 1-WL equals unfolding equivalence. On the other hand, GNNs turned out to be universal approximators on graphs modulo the constraints enforced by 1-WL/unfolding equivalence. However, these results only apply to Static Undirected Homogeneous Graphs with node attributes. In contrast, real-life applications often involve a variety of graph properties, such as, e.g., dynamics or node and edge attributes. In this paper, we conduct a theoretical analysis of the expressive power of GNNs for these two graph types that are particularly of interest. Dynamic graphs are widely used in modern applications, and its theoretical analysis requires new approaches. The attributed type acts as a standard form for all graph types since it has been shown that all graph types can be transformed without loss to Static Undirected Homogeneous Graphs with attributes on nodes and edges (SAUHG). The study considers generic GNN models and proposes appropriate 1-WL tests for those domains. Then, the results on the expressive power of GNNs are extended by proving that GNNs have the same capability as the 1-WL test in distinguishing dynamic and attributed graphs, the 1-WL equivalence equals unfolding equivalence and that GNNs are universal approximators modulo 1-WL/unfolding equivalence. Moreover, the proof of the approximation capability holds for SAUHGs, which include most of those used in practical applications, and it is constructive in nature allowing to deduce hints on the architecture of GNNs that can achieve the desired accuracy.

FDGNN: Fully Dynamic Graph Neural Network

Dynamic Graph Neural Networks recently became more and more important as graphs from many scientific fields, ranging from mathematics, biology, social sciences, and physics to computer science, are dynamic by nature. While temporal changes (dynamics) play an essential role in many real-world applications, most of the models in the literature on Graph Neural Networks (GNN) process static graphs. The few GNN models on dynamic graphs only consider exceptional cases of dynamics, e.g., node attribute-dynamic graphs or structure-dynamic graphs limited to additions or changes to the graph's edges, etc. Therefore, we present a novel Fully Dynamic Graph Neural Network (FDGNN) that can handle fully-dynamic graphs in continuous time. The proposed method provides a node and an edge embedding that includes their activity to address added and deleted nodes or edges, and possible attributes. Furthermore, the embeddings specify Temporal Point Processes for each event to encode the distributions of the structure- and attribute-related incoming graph events. In addition, our model can be updated efficiently by considering single events for local retraining.

Graph Neural Networks Designed for Different Graph Types: A Survey

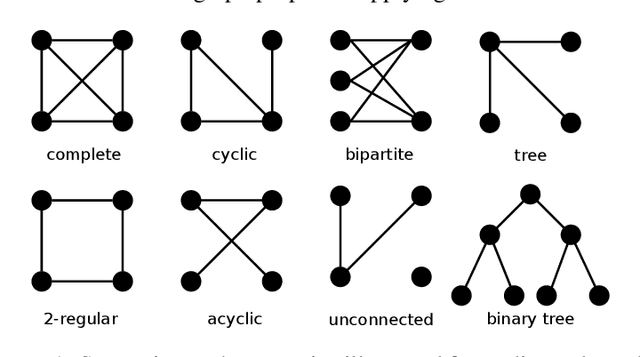
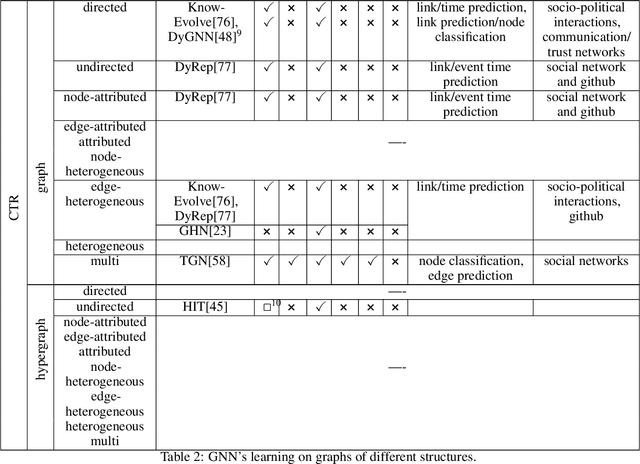
Graphs are ubiquitous in nature and can therefore serve as models for many practical but also theoretical problems. Based on this, the young research field of Graph Neural Networks (GNNs) has emerged. Despite the youth of the field and the speed in which new models are developed, many good surveys have been published in the last years. Nevertheless, an overview on which graph types can be modeled by GNNs is missing. In this survey, we give a detailed overview of already existing GNNs and, unlike previous surveys, categorize them according to their ability to handle different graph types. We consider GNNs operating on static as well as on dynamic graphs of different structural constitutions, with or without node or edge attributes. Moreover in the dynamic case, we separate the models in discrete-time and continuous-time dynamic graphs based on their architecture. According to our findings, there are still graph types, that are not covered by existing GNN models. Specifically, models concerning heterogeneity in attributes are missing and the deletion of nodes and edges is only covered rarely.

Multi-Sensor Data and Knowledge Fusion -- A Proposal for a Terminology Definition

Fusion is a common tool for the analysis and utilization of available datasets and so an essential part of data mining and machine learning processes. However, a clear definition of the type of fusion is not always provided due to inconsistent literature. In the following, the process of fusion is defined depending on the fusion components and the abstraction level on which the fusion occurs. The focus in the first part of the paper at hand is on the clear definition of the terminology and the development of an appropriate ontology of the fusion components and the fusion level. In the second part, common fusion techniques are presented.