ALINC: Active Learning for Inductive Node Classification via Graph Sampling

Active learning (AL) for node classification typically focuses on selecting the most informative nodes for annotation within one or a few large graphs (e.g., in social network analysis). However, in other domains, such as molecular chemistry or electronic design automation, datasets consist of thousands of independent graphs. In many of these inductive settings, annotating an individual node requires a full-graph analysis, which effectively yields the remaining node labels on-the-fly. Therefore, these scenarios require AL strategies that select entire graphs instead of single nodes, a problem which has not been tackled in the literature so far. Thus, we introduce ALINC, an AL framework for inductive node classification via graph sampling. It bridges the existing methodological gap by elevating node-level utility measures to graph-level selection criteria through various aggregation mechanisms. In an extensive benchmark including ten strategies, three aggregation methods, and four datasets, we identify CoreSet, TypiClust, and BADGE as the top-performing graph sampling strategies. Our detailed analysis further reveals that the choice of the aggregation method is pivotal, as it substantially affects model performance and annotation costs. Finally, we demonstrate the effectiveness of ALINC in two use case studies: site-of-metabolism prediction in molecules and design automation of printed circuit board schematics.

Graph Neural Networks for Automatic Addition of Optimizing Components in Printed Circuit Board Schematics

The design and optimization of Printed Circuit Board (PCB) schematics is crucial for the development of high-quality electronic devices. Thereby, an important task is to optimize drafts by adding components that improve the robustness and reliability of the circuit, e.g., pull-up resistors or decoupling capacitors. Since there is a shortage of skilled engineers and manual optimizations are very time-consuming, these best practices are often neglected. However, this typically leads to higher costs for troubleshooting in later development stages as well as shortened product life cycles, resulting in an increased amount of electronic waste that is difficult to recycle. Here, we present an approach for automating the addition of new components into PCB schematics by representing them as bipartite graphs and utilizing a node pair prediction model based on Graph Neural Networks (GNNs). We apply our approach to three highly relevant PCB design optimization tasks and compare the performance of several popular GNN architectures on real-world datasets labeled by human experts. We show that GNNs can solve these problems with high accuracy and demonstrate that our approach offers the potential to automate PCB design optimizations in a time- and cost-efficient manner.

Flow-Attentional Graph Neural Networks

Graph Neural Networks (GNNs) have become essential for learning from graph-structured data. However, existing GNNs do not consider the conservation law inherent in graphs associated with a flow of physical resources, such as electrical current in power grids or traffic in transportation networks, which can lead to reduced model performance. To address this, we propose flow attention, which adapts existing graph attention mechanisms to satisfy Kirchhoff\'s first law. Furthermore, we discuss how this modification influences the expressivity and identify sets of non-isomorphic graphs that can be discriminated by flow attention but not by standard attention. Through extensive experiments on two flow graph datasets (electronic circuits and power grids), we demonstrate that flow attention enhances the performance of attention-based GNNs on both graph-level classification and regression tasks.

FDGNN: Fully Dynamic Graph Neural Network

Dynamic Graph Neural Networks recently became more and more important as graphs from many scientific fields, ranging from mathematics, biology, social sciences, and physics to computer science, are dynamic by nature. While temporal changes (dynamics) play an essential role in many real-world applications, most of the models in the literature on Graph Neural Networks (GNN) process static graphs. The few GNN models on dynamic graphs only consider exceptional cases of dynamics, e.g., node attribute-dynamic graphs or structure-dynamic graphs limited to additions or changes to the graph's edges, etc. Therefore, we present a novel Fully Dynamic Graph Neural Network (FDGNN) that can handle fully-dynamic graphs in continuous time. The proposed method provides a node and an edge embedding that includes their activity to address added and deleted nodes or edges, and possible attributes. Furthermore, the embeddings specify Temporal Point Processes for each event to encode the distributions of the structure- and attribute-related incoming graph events. In addition, our model can be updated efficiently by considering single events for local retraining.

Graph Neural Networks Designed for Different Graph Types: A Survey

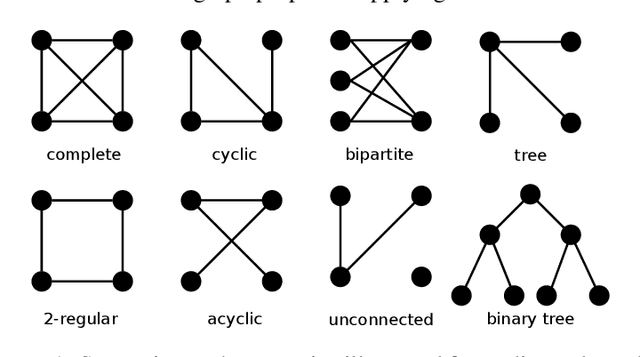
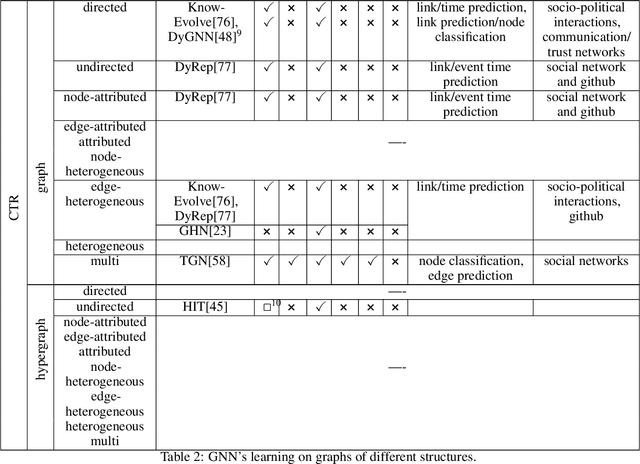
Graphs are ubiquitous in nature and can therefore serve as models for many practical but also theoretical problems. Based on this, the young research field of Graph Neural Networks (GNNs) has emerged. Despite the youth of the field and the speed in which new models are developed, many good surveys have been published in the last years. Nevertheless, an overview on which graph types can be modeled by GNNs is missing. In this survey, we give a detailed overview of already existing GNNs and, unlike previous surveys, categorize them according to their ability to handle different graph types. We consider GNNs operating on static as well as on dynamic graphs of different structural constitutions, with or without node or edge attributes. Moreover in the dynamic case, we separate the models in discrete-time and continuous-time dynamic graphs based on their architecture. According to our findings, there are still graph types, that are not covered by existing GNN models. Specifically, models concerning heterogeneity in attributes are missing and the deletion of nodes and edges is only covered rarely.