Enhancing Embedding Representations of Biomedical Data using Logic Knowledge

Knowledge Graph Embeddings (KGE) have become a quite popular class of models specifically devised to deal with ontologies and graph structure data, as they can implicitly encode statistical dependencies between entities and relations in a latent space. KGE techniques are particularly effective for the biomedical domain, where it is quite common to deal with large knowledge graphs underlying complex interactions between biological and chemical objects. Recently in the literature, the PharmKG dataset has been proposed as one of the most challenging knowledge graph biomedical benchmark, with hundreds of thousands of relational facts between genes, diseases and chemicals. Despite KGEs can scale to very large relational domains, they generally fail at representing more complex relational dependencies between facts, like logic rules, which may be fundamental in complex experimental settings. In this paper, we exploit logic rules to enhance the embedding representations of KGEs on the PharmKG dataset. To this end, we adopt Relational Reasoning Network (R2N), a recently proposed neural-symbolic approach showing promising results on knowledge graph completion tasks. An R2N uses the available logic rules to build a neural architecture that reasons over KGE latent representations. In the experiments, we show that our approach is able to significantly improve the current state-of-the-art on the PharmKG dataset. Finally, we provide an ablation study to experimentally compare the effect of alternative sets of rules according to different selection criteria and varying the number of considered rules.

Weisfeiler--Lehman goes Dynamic: An Analysis of the Expressive Power of Graph Neural Networks for Attributed and Dynamic Graphs

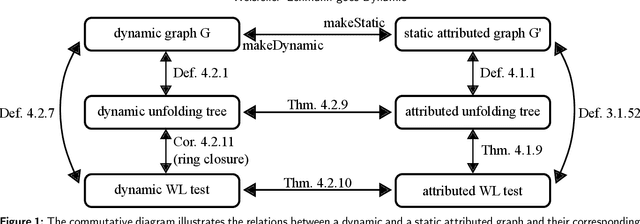
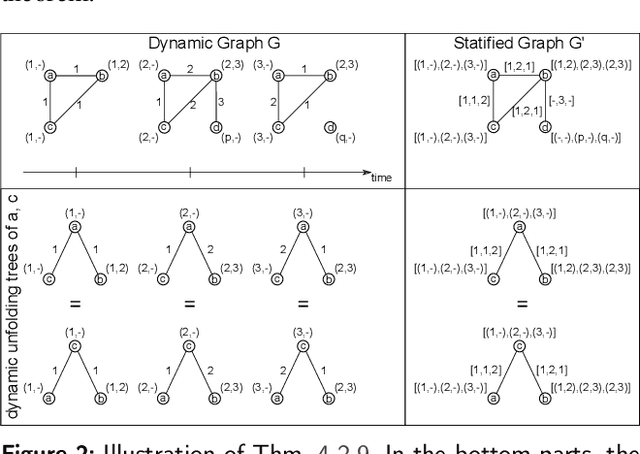
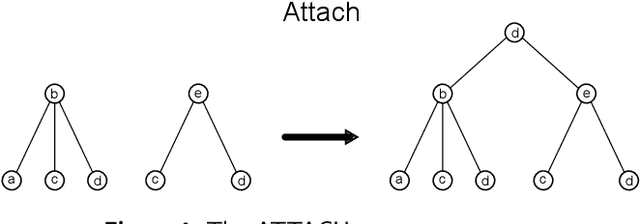
Graph Neural Networks (GNNs) are a large class of relational models for graph processing. Recent theoretical studies on the expressive power of GNNs have focused on two issues. On the one hand, it has been proven that GNNs are as powerful as the Weisfeiler-Lehman test (1-WL) in their ability to distinguish graphs. Moreover, it has been shown that the equivalence enforced by 1-WL equals unfolding equivalence. On the other hand, GNNs turned out to be universal approximators on graphs modulo the constraints enforced by 1-WL/unfolding equivalence. However, these results only apply to Static Undirected Homogeneous Graphs with node attributes. In contrast, real-life applications often involve a variety of graph properties, such as, e.g., dynamics or node and edge attributes. In this paper, we conduct a theoretical analysis of the expressive power of GNNs for these two graph types that are particularly of interest. Dynamic graphs are widely used in modern applications, and its theoretical analysis requires new approaches. The attributed type acts as a standard form for all graph types since it has been shown that all graph types can be transformed without loss to Static Undirected Homogeneous Graphs with attributes on nodes and edges (SAUHG). The study considers generic GNN models and proposes appropriate 1-WL tests for those domains. Then, the results on the expressive power of GNNs are extended by proving that GNNs have the same capability as the 1-WL test in distinguishing dynamic and attributed graphs, the 1-WL equivalence equals unfolding equivalence and that GNNs are universal approximators modulo 1-WL/unfolding equivalence. Moreover, the proof of the approximation capability holds for SAUHGs, which include most of those used in practical applications, and it is constructive in nature allowing to deduce hints on the architecture of GNNs that can achieve the desired accuracy.