FreeSeg-Diff: Training-Free Open-Vocabulary Segmentation with Diffusion Models

Foundation models have exhibited unprecedented capabilities in tackling many domains and tasks. Models such as CLIP are currently widely used to bridge cross-modal representations, and text-to-image diffusion models are arguably the leading models in terms of realistic image generation. Image generative models are trained on massive datasets that provide them with powerful internal spatial representations. In this work, we explore the potential benefits of such representations, beyond image generation, in particular, for dense visual prediction tasks. We focus on the task of image segmentation, which is traditionally solved by training models on closed-vocabulary datasets, with pixel-level annotations. To avoid the annotation cost or training large diffusion models, we constraint our setup to be zero-shot and training-free. In a nutshell, our pipeline leverages different and relatively small-sized, open-source foundation models for zero-shot open-vocabulary segmentation. The pipeline is as follows: the image is passed to both a captioner model (i.e. BLIP) and a diffusion model (i.e., Stable Diffusion Model) to generate a text description and visual representation, respectively. The features are clustered and binarized to obtain class agnostic masks for each object. These masks are then mapped to a textual class, using the CLIP model to support open-vocabulary. Finally, we add a refinement step that allows to obtain a more precise segmentation mask. Our approach (dubbed FreeSeg-Diff), which does not rely on any training, outperforms many training-based approaches on both Pascal VOC and COCO datasets. In addition, we show very competitive results compared to the recent weakly-supervised segmentation approaches. We provide comprehensive experiments showing the superiority of diffusion model features compared to other pretrained models. Project page: https://bcorrad.github.io/freesegdiff/

VC dimension of Graph Neural Networks with Pfaffian activation functions

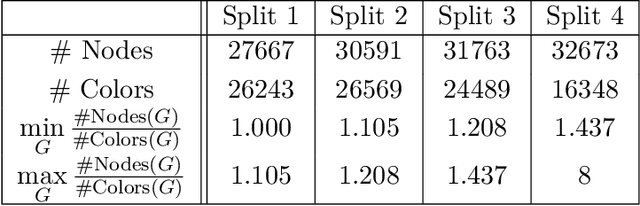
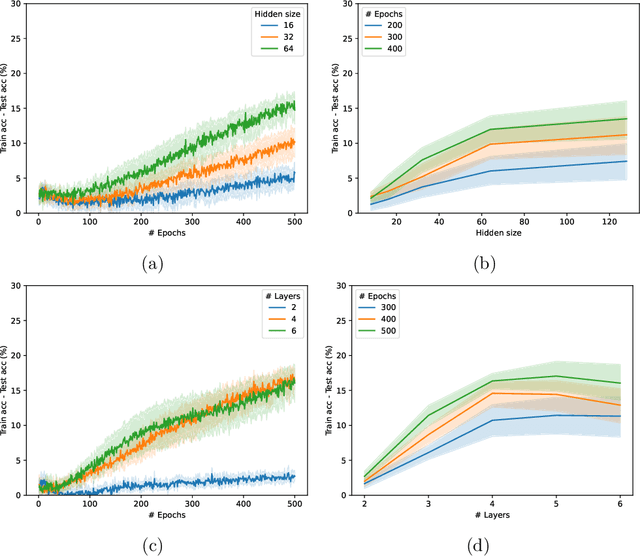
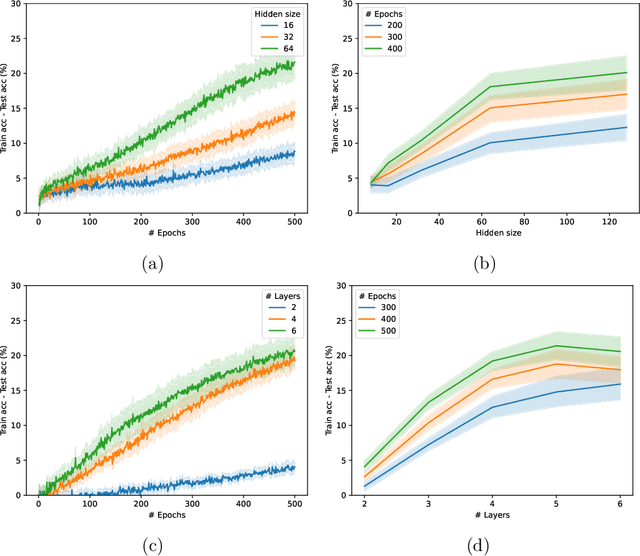
Graph Neural Networks (GNNs) have emerged in recent years as a powerful tool to learn tasks across a wide range of graph domains in a data-driven fashion; based on a message passing mechanism, GNNs have gained increasing popularity due to their intuitive formulation, closely linked with the Weisfeiler-Lehman (WL) test for graph isomorphism, to which they have proven equivalent. From a theoretical point of view, GNNs have been shown to be universal approximators, and their generalization capability (namely, bounds on the Vapnik Chervonekis (VC) dimension) has recently been investigated for GNNs with piecewise polynomial activation functions. The aim of our work is to extend this analysis on the VC dimension of GNNs to other commonly used activation functions, such as sigmoid and hyperbolic tangent, using the framework of Pfaffian function theory. Bounds are provided with respect to architecture parameters (depth, number of neurons, input size) as well as with respect to the number of colors resulting from the 1-WL test applied on the graph domain. The theoretical analysis is supported by a preliminary experimental study.

A topological description of loss surfaces based on Betti Numbers

In the context of deep learning models, attention has recently been paid to studying the surface of the loss function in order to better understand training with methods based on gradient descent. This search for an appropriate description, both analytical and topological, has led to numerous efforts to identify spurious minima and characterize gradient dynamics. Our work aims to contribute to this field by providing a topological measure to evaluate loss complexity in the case of multilayer neural networks. We compare deep and shallow architectures with common sigmoidal activation functions by deriving upper and lower bounds on the complexity of their loss function and revealing how that complexity is influenced by the number of hidden units, training models, and the activation function used. Additionally, we found that certain variations in the loss function or model architecture, such as adding an $\ell_2$ regularization term or implementing skip connections in a feedforward network, do not affect loss topology in specific cases.

SortNet: Learning To Rank By a Neural-Based Sorting Algorithm

The problem of relevance ranking consists of sorting a set of objects with respect to a given criterion. Since users may prefer different relevance criteria, the ranking algorithms should be adaptable to the user needs. Two main approaches exist in literature for the task of learning to rank: 1) a score function, learned by examples, which evaluates the properties of each object yielding an absolute relevance value that can be used to order the objects or 2) a pairwise approach, where a "preference function" is learned using pairs of objects to define which one has to be ranked first. In this paper, we present SortNet, an adaptive ranking algorithm which orders objects using a neural network as a comparator. The neural network training set provides examples of the desired ordering between pairs of items and it is constructed by an iterative procedure which, at each iteration, adds the most informative training examples. Moreover, the comparator adopts a connectionist architecture that is particularly suited for implementing a preference function. We also prove that such an architecture has the universal approximation property and can implement a wide class of functions. Finally, the proposed algorithm is evaluated on the LETOR dataset showing promising performances in comparison with other state of the art algorithms.

Graph Neural Networks for temporal graphs: State of the art, open challenges, and opportunities

Graph Neural Networks (GNNs) have become the leading paradigm for learning on (static) graph-structured data. However, many real-world systems are dynamic in nature, since the graph and node/edge attributes change over time. In recent years, GNN-based models for temporal graphs have emerged as a promising area of research to extend the capabilities of GNNs. In this work, we provide the first comprehensive overview of the current state-of-the-art of temporal GNN, introducing a rigorous formalization of learning settings and tasks and a novel taxonomy categorizing existing approaches in terms of how the temporal aspect is represented and processed. We conclude the survey with a discussion of the most relevant open challenges for the field, from both research and application perspectives.

Weisfeiler--Lehman goes Dynamic: An Analysis of the Expressive Power of Graph Neural Networks for Attributed and Dynamic Graphs

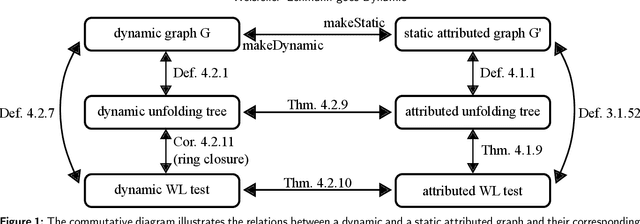
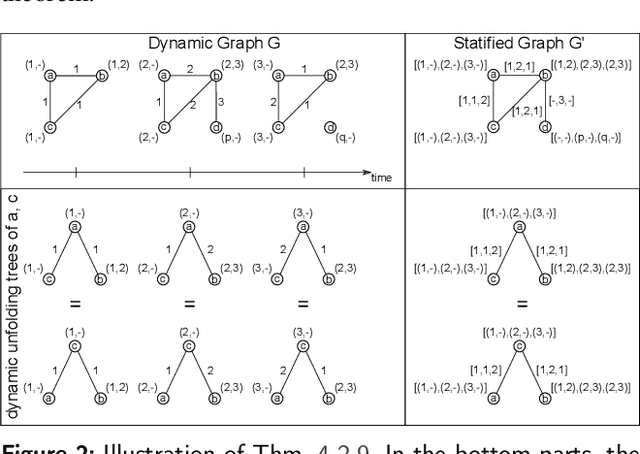
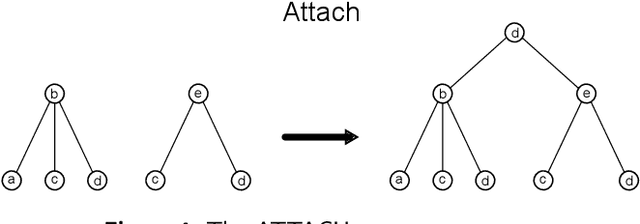
Graph Neural Networks (GNNs) are a large class of relational models for graph processing. Recent theoretical studies on the expressive power of GNNs have focused on two issues. On the one hand, it has been proven that GNNs are as powerful as the Weisfeiler-Lehman test (1-WL) in their ability to distinguish graphs. Moreover, it has been shown that the equivalence enforced by 1-WL equals unfolding equivalence. On the other hand, GNNs turned out to be universal approximators on graphs modulo the constraints enforced by 1-WL/unfolding equivalence. However, these results only apply to Static Undirected Homogeneous Graphs with node attributes. In contrast, real-life applications often involve a variety of graph properties, such as, e.g., dynamics or node and edge attributes. In this paper, we conduct a theoretical analysis of the expressive power of GNNs for these two graph types that are particularly of interest. Dynamic graphs are widely used in modern applications, and its theoretical analysis requires new approaches. The attributed type acts as a standard form for all graph types since it has been shown that all graph types can be transformed without loss to Static Undirected Homogeneous Graphs with attributes on nodes and edges (SAUHG). The study considers generic GNN models and proposes appropriate 1-WL tests for those domains. Then, the results on the expressive power of GNNs are extended by proving that GNNs have the same capability as the 1-WL test in distinguishing dynamic and attributed graphs, the 1-WL equivalence equals unfolding equivalence and that GNNs are universal approximators modulo 1-WL/unfolding equivalence. Moreover, the proof of the approximation capability holds for SAUHGs, which include most of those used in practical applications, and it is constructive in nature allowing to deduce hints on the architecture of GNNs that can achieve the desired accuracy.

Modular multi-source prediction of drug side-effects with DruGNN

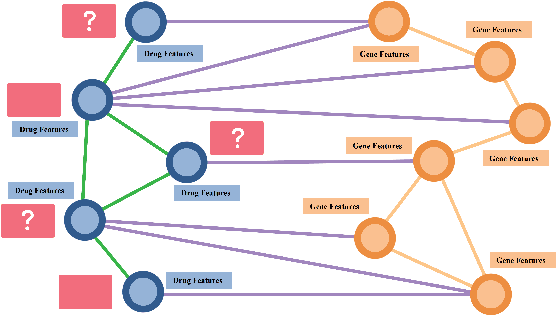
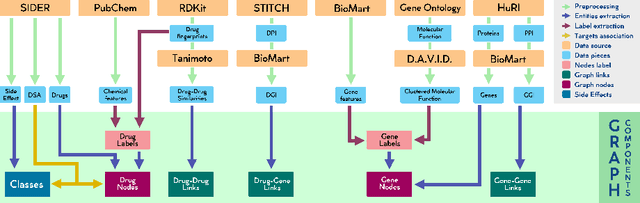
Drug Side-Effects (DSEs) have a high impact on public health, care system costs, and drug discovery processes. Predicting the probability of side-effects, before their occurrence, is fundamental to reduce this impact, in particular on drug discovery. Candidate molecules could be screened before undergoing clinical trials, reducing the costs in time, money, and health of the participants. Drug side-effects are triggered by complex biological processes involving many different entities, from drug structures to protein-protein interactions. To predict their occurrence, it is necessary to integrate data from heterogeneous sources. In this work, such heterogeneous data is integrated into a graph dataset, expressively representing the relational information between different entities, such as drug molecules and genes. The relational nature of the dataset represents an important novelty for drug side-effect predictors. Graph Neural Networks (GNNs) are exploited to predict DSEs on our dataset with very promising results. GNNs are deep learning models that can process graph-structured data, with minimal information loss, and have been applied on a wide variety of biological tasks. Our experimental results confirm the advantage of using relationships between data entities, suggesting interesting future developments in this scope. The experimentation also shows the importance of specific subsets of data in determining associations between drugs and side-effects.

Graph Neural Networks for Communication Networks: Context, Use Cases and Opportunities

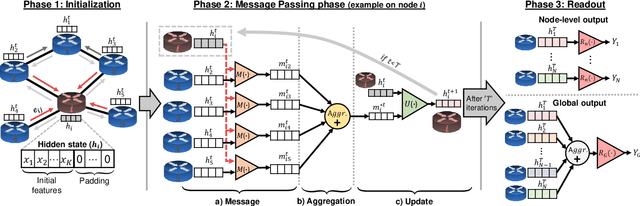
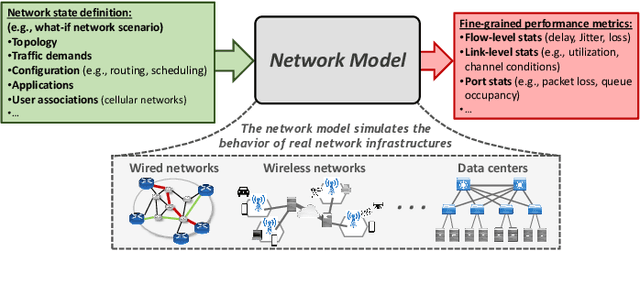
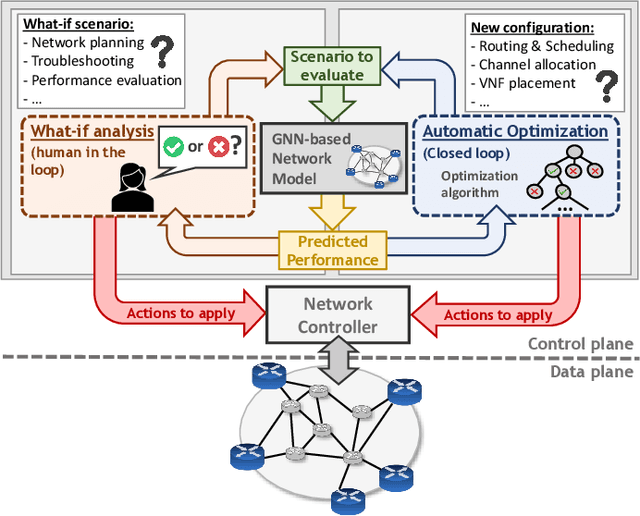
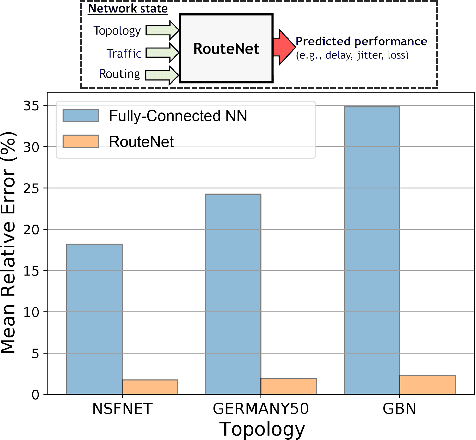
Graph neural networks (GNN) have shown outstanding applications in many fields where data is fundamentally represented as graphs (e.g., chemistry, biology, recommendation systems). In this vein, communication networks comprise many fundamental components that are naturally represented in a graph-structured manner (e.g., topology, configurations, traffic flows). This position article presents GNNs as a fundamental tool for modeling, control and management of communication networks. GNNs represent a new generation of data-driven models that can accurately learn and reproduce the complex behaviors behind real networks. As a result, such models can be applied to a wide variety of networking use cases, such as planning, online optimization, or troubleshooting. The main advantage of GNNs over traditional neural networks lies in its unprecedented generalization capabilities when applied to other networks and configurations unseen during training, which is a critical feature for achieving practical data-driven solutions for networking. This article comprises a brief tutorial on GNNs and their possible applications to communication networks. To showcase the potential of this technology, we present two use cases with state-of-the-art GNN models respectively applied to wired and wireless networks. Lastly, we delve into the key open challenges and opportunities yet to be explored in this novel research area.

A unifying point of view on expressive power of GNNs

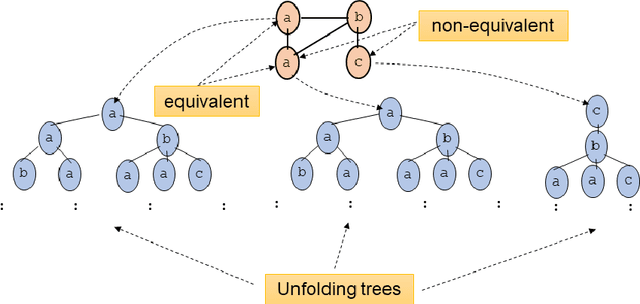
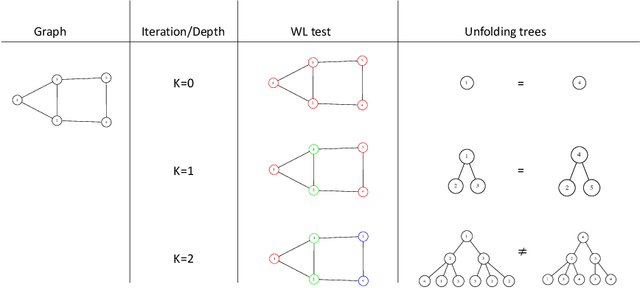
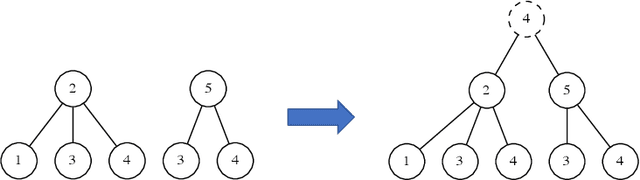
Graph Neural Networks (GNNs) are a wide class of connectionist models for graph processing. They perform an iterative message passing operation on each node and its neighbors, to solve classification/ clustering tasks -- on some nodes or on the whole graph -- collecting all such messages, regardless of their order. Despite the differences among the various models belonging to this class, most of them adopt the same computation scheme, based on a local aggregation mechanism and, intuitively, the local computation framework is mainly responsible for the expressive power of GNNs. In this paper, we prove that the Weisfeiler--Lehman test induces an equivalence relationship on the graph nodes that exactly corresponds to the unfolding equivalence, defined on the original GNN model. Therefore, the results on the expressive power of the original GNNs can be extended to general GNNs which, under mild conditions, can be proved capable of approximating, in probability and up to any precision, any function on graphs that respects the unfolding equivalence.

A multi-stage GAN for multi-organ chest X-ray image generation and segmentation

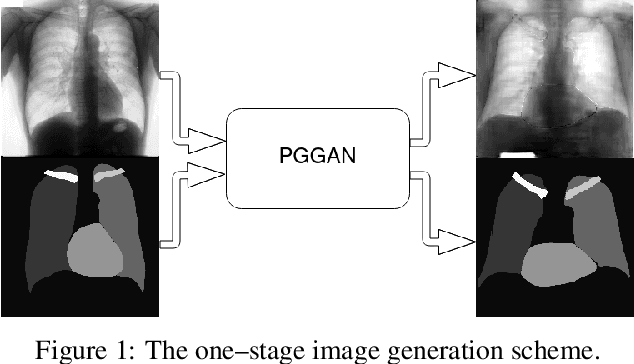
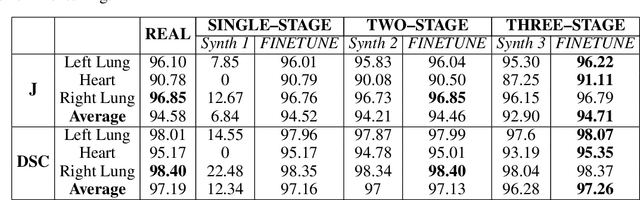
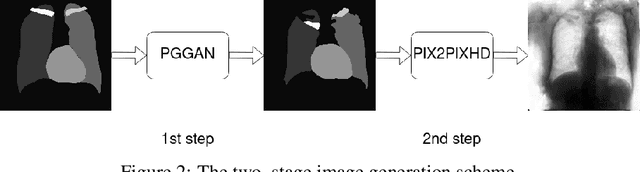
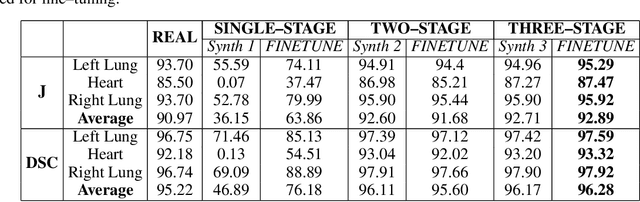
Multi-organ segmentation of X-ray images is of fundamental importance for computer aided diagnosis systems. However, the most advanced semantic segmentation methods rely on deep learning and require a huge amount of labeled images, which are rarely available due to both the high cost of human resources and the time required for labeling. In this paper, we present a novel multi-stage generation algorithm based on Generative Adversarial Networks (GANs) that can produce synthetic images along with their semantic labels and can be used for data augmentation. The main feature of the method is that, unlike other approaches, generation occurs in several stages, which simplifies the procedure and allows it to be used on very small datasets. The method has been evaluated on the segmentation of chest radiographic images, showing promising results. The multistage approach achieves state-of-the-art and, when very few images are used to train the GANs, outperforms the corresponding single-stage approach.