VC dimension of Graph Neural Networks with Pfaffian activation functions
Paper and Code
Jan 22, 2024
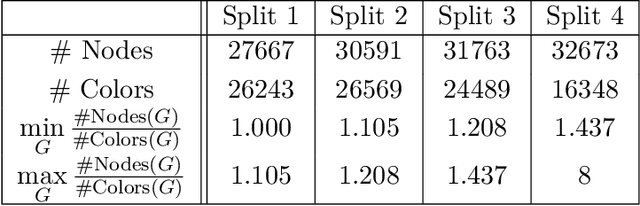
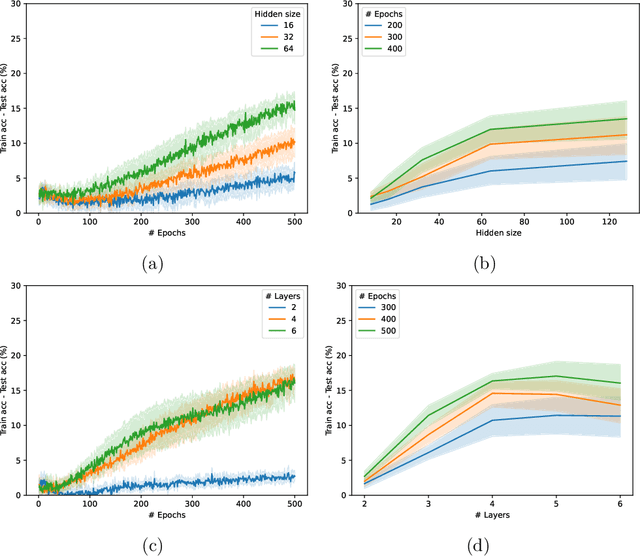
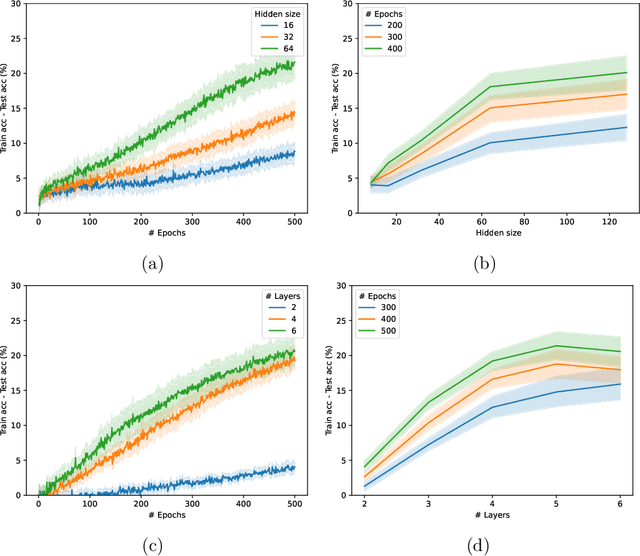
Graph Neural Networks (GNNs) have emerged in recent years as a powerful tool to learn tasks across a wide range of graph domains in a data-driven fashion; based on a message passing mechanism, GNNs have gained increasing popularity due to their intuitive formulation, closely linked with the Weisfeiler-Lehman (WL) test for graph isomorphism, to which they have proven equivalent. From a theoretical point of view, GNNs have been shown to be universal approximators, and their generalization capability (namely, bounds on the Vapnik Chervonekis (VC) dimension) has recently been investigated for GNNs with piecewise polynomial activation functions. The aim of our work is to extend this analysis on the VC dimension of GNNs to other commonly used activation functions, such as sigmoid and hyperbolic tangent, using the framework of Pfaffian function theory. Bounds are provided with respect to architecture parameters (depth, number of neurons, input size) as well as with respect to the number of colors resulting from the 1-WL test applied on the graph domain. The theoretical analysis is supported by a preliminary experimental study.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge