Angular separability of data clusters or network communities in geometrical space and its relevance to hyperbolic embedding

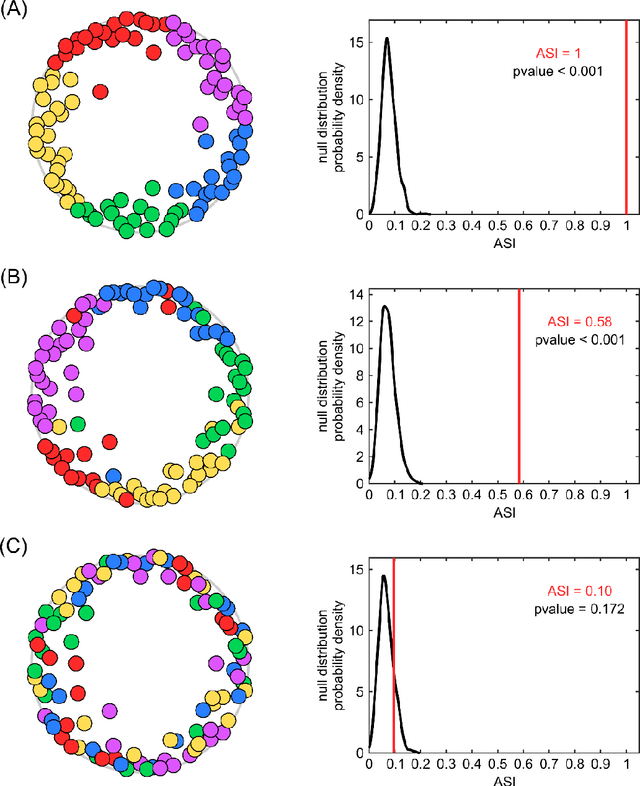
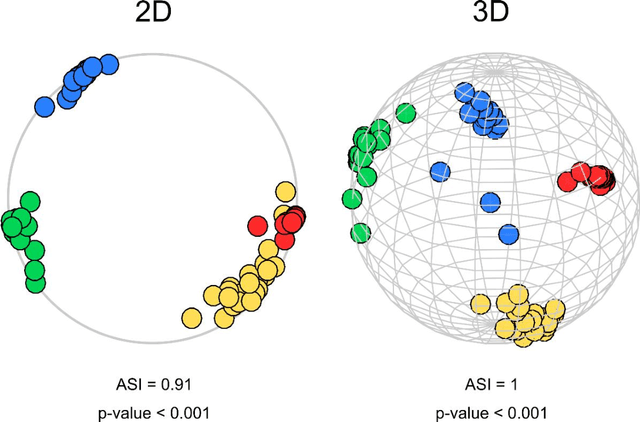
Analysis of 'big data' characterized by high-dimensionality such as word vectors and complex networks requires often their representation in a geometrical space by embedding. Recent developments in machine learning and network geometry have pointed out the hyperbolic space as a useful framework for the representation of this data derived by real complex physical systems. In the hyperbolic space, the radial coordinate of the nodes characterizes their hierarchy, whereas the angular distance between them represents their similarity. Several studies have highlighted the relationship between the angular coordinates of the nodes embedded in the hyperbolic space and the community metadata available. However, such analyses have been often limited to a visual or qualitative assessment. Here, we introduce the angular separation index (ASI), to quantitatively evaluate the separation of node network communities or data clusters over the angular coordinates of a geometrical space. ASI is particularly useful in the hyperbolic space - where it is extensively tested along this study - but can be used in general for any assessment of angular separation regardless of the adopted geometry. ASI is proposed together with an exact test statistic based on a uniformly random null model to assess the statistical significance of the separation. We show that ASI allows to discover two significant phenomena in network geometry. The first is that the increase of temperature in 2D hyperbolic network generative models, not only reduces the network clustering but also induces a 'dimensionality jump' of the network to dimensions higher than two. The second is that ASI can be successfully applied to detect the intrinsic dimensionality of network structures that grow in a hidden geometrical space.

Latent Geometry Inspired Graph Dissimilarities Enhance Affinity Propagation Community Detection in Complex Networks

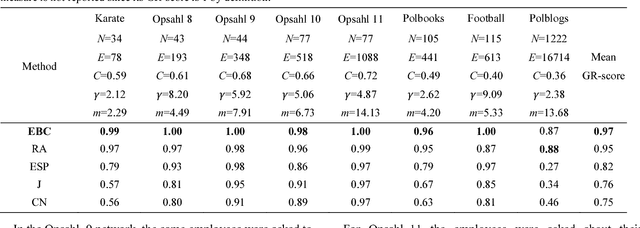
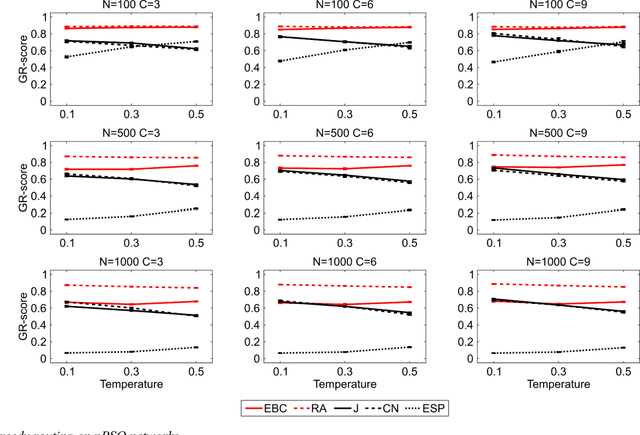
Affinity propagation is one of the most effective unsupervised pattern recognition algorithms for data clustering in high-dimensional feature space. However, the numerous attempts to test its performance for community detection in complex networks have been attaining results very far from the state of the art methods such as Infomap and Louvain. Yet, all these studies agreed that the crucial problem is to convert the unweighted network topology in a 'smart-enough' node dissimilarity matrix that is able to properly address the message passing procedure behind affinity propagation clustering. Here we introduce a conceptual innovation and we discuss how to leverage network latent geometry notions in order to design dissimilarity matrices for affinity propagation community detection. Our results demonstrate that the latent geometry inspired dissimilarity measures we design bring affinity propagation to equal or outperform current state of the art methods for community detection. These findings are solidly proven considering both synthetic 'realistic' networks (with known ground-truth communities) and real networks (with community metadata), even when the data structure is corrupted by noise artificially induced by missing or spurious connectivity.

Machine learning meets network science: dimensionality reduction for fast and efficient embedding of networks in the hyperbolic space

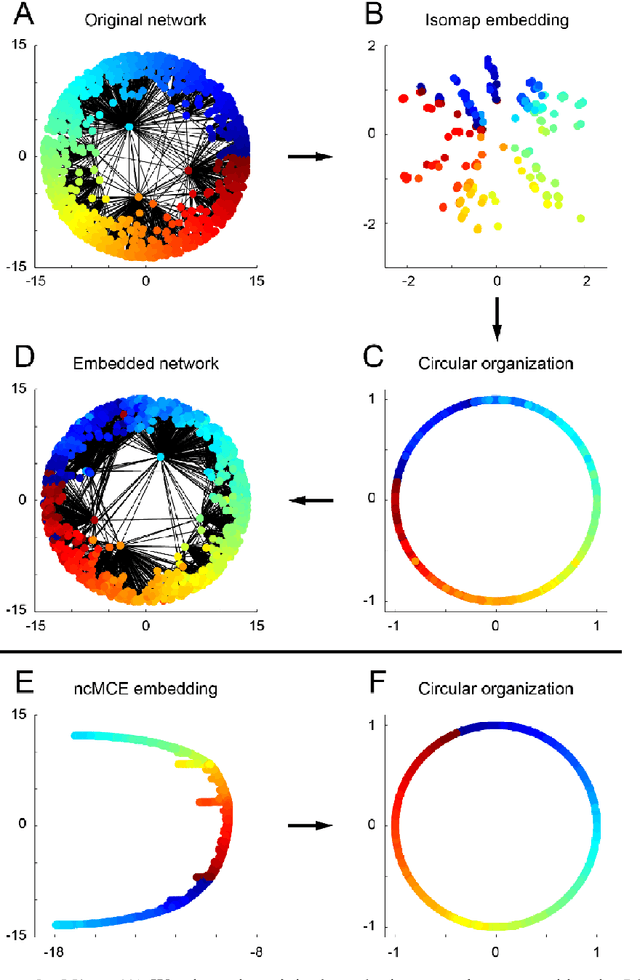
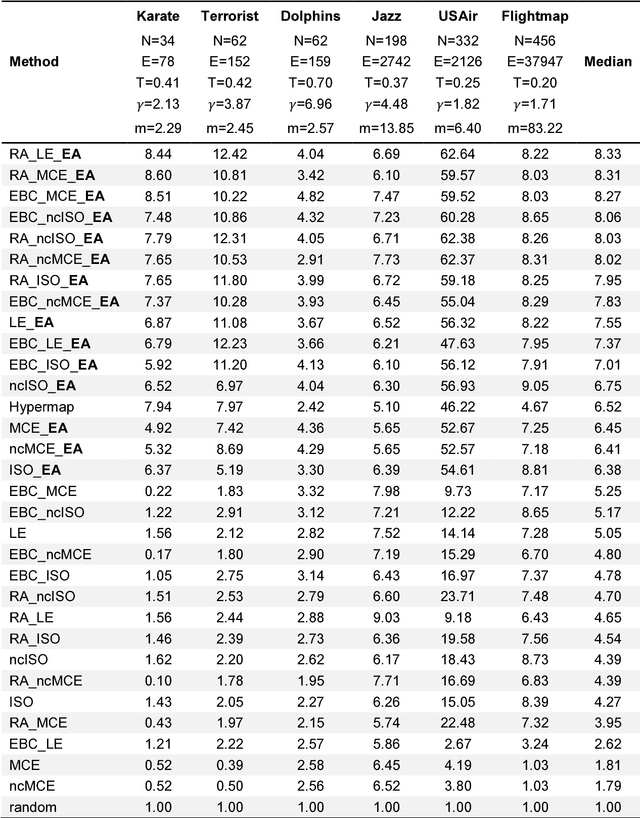
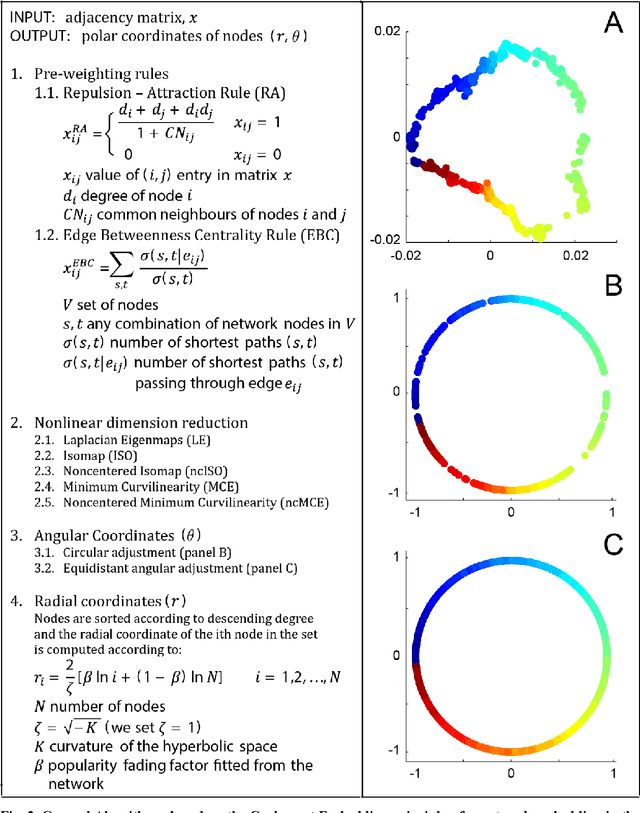
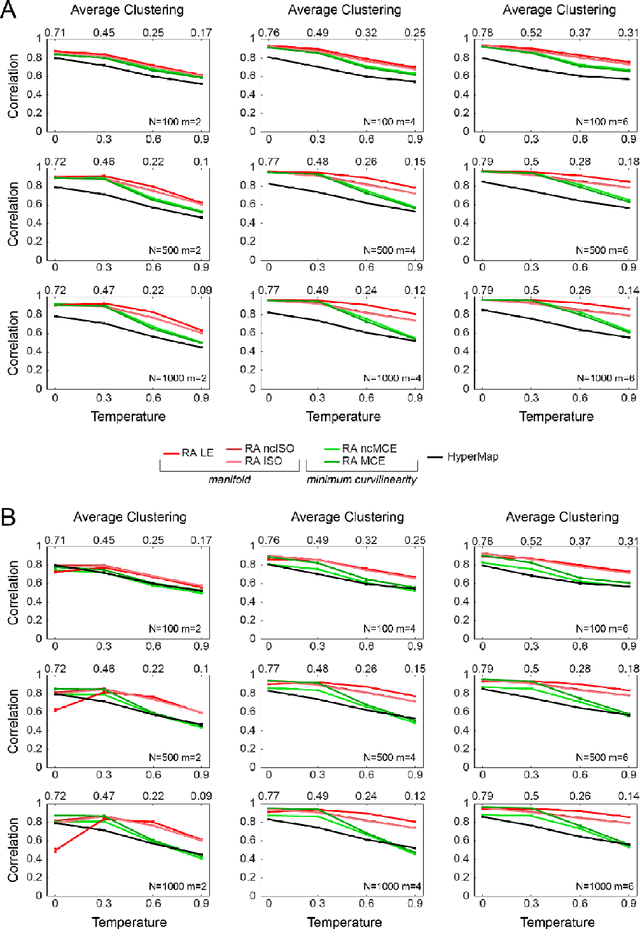
Complex network topologies and hyperbolic geometry seem specularly connected, and one of the most fascinating and challenging problems of recent complex network theory is to map a given network to its hyperbolic space. The Popularity Similarity Optimization (PSO) model represents - at the moment - the climax of this theory. It suggests that the trade-off between node popularity and similarity is a mechanism to explain how complex network topologies emerge - as discrete samples - from the continuous world of hyperbolic geometry. The hyperbolic space seems appropriate to represent real complex networks. In fact, it preserves many of their fundamental topological properties, and can be exploited for real applications such as, among others, link prediction and community detection. Here, we observe for the first time that a topological-based machine learning class of algorithms - for nonlinear unsupervised dimensionality reduction - can directly approximate the network's node angular coordinates of the hyperbolic model into a two-dimensional space, according to a similar topological organization that we named angular coalescence. On the basis of this phenomenon, we propose a new class of algorithms that offers fast and accurate coalescent embedding of networks in the hyperbolic space even for graphs with thousands of nodes.