Cell Mechanics Based Computational Classification of Red Blood Cells Via Machine Intelligence Applied to Morpho-Rheological Markers

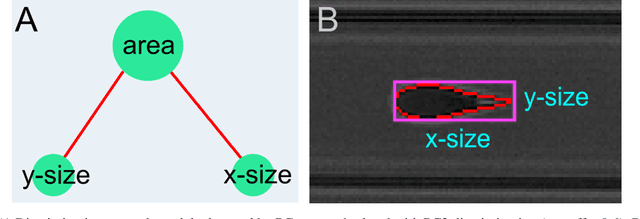
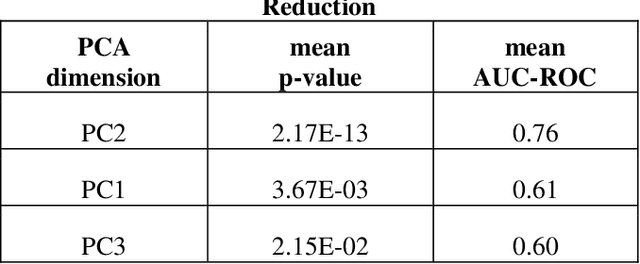
Despite fluorescent cell-labelling being widely employed in biomedical studies, some of its drawbacks are inevitable, with unsuitable fluorescent probes or probes inducing a functional change being the main limitations. Consequently, the demand for and development of label-free methodologies to classify cells is strong and its impact on precision medicine is relevant. Towards this end, high-throughput techniques for cell mechanical phenotyping have been proposed to get a multidimensional biophysical characterization of single cells. With this motivation, our goal here is to investigate the extent to which an unsupervised machine learning methodology, which is applied exclusively on morpho-rheological markers obtained by real-time deformability and fluorescence cytometry (RT-FDC), can address the difficult task of providing label-free discrimination of reticulocytes from mature red blood cells. We focused on this problem, since the characterization of reticulocytes (their percentage and cellular features) in the blood is vital in multiple human disease conditions, especially bone-marrow disorders such as anemia and leukemia. Our approach reports promising label-free results in the classification of reticulocytes from mature red blood cells, and it represents a step forward in the development of high-throughput morpho-rheological-based methodologies for the computational categorization of single cells. Besides, our methodology can be an alternative but also a complementary method to integrate with existing cell-labelling techniques.

Machine learning meets network science: dimensionality reduction for fast and efficient embedding of networks in the hyperbolic space

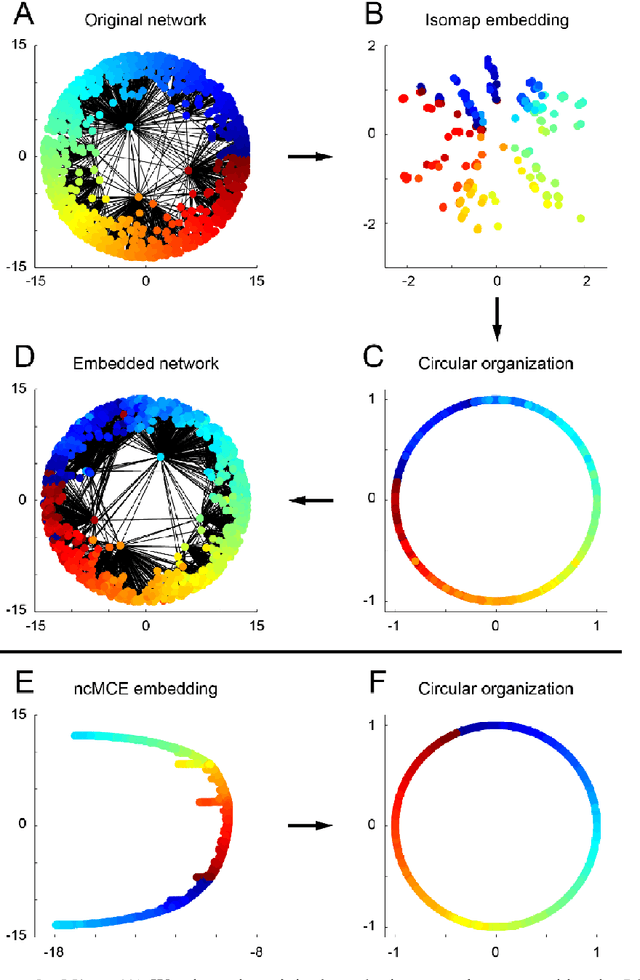
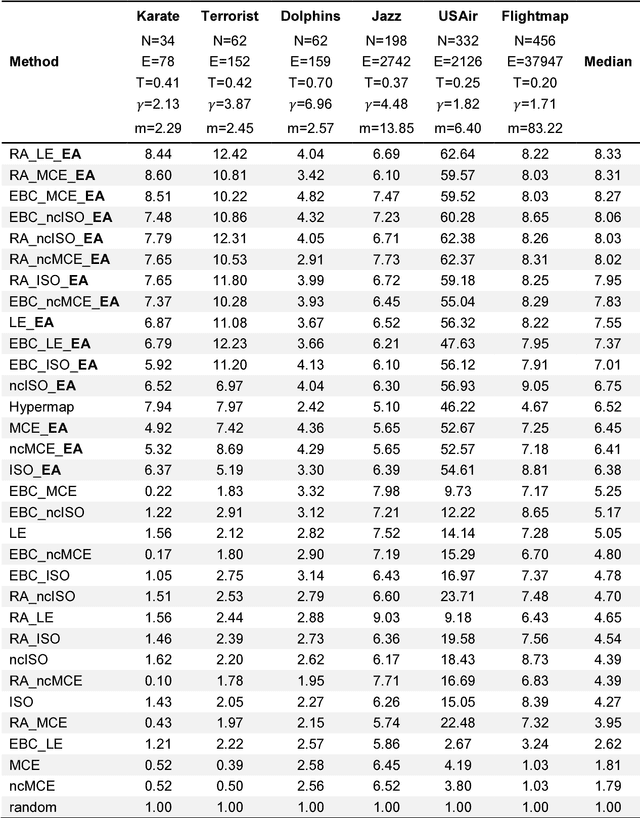
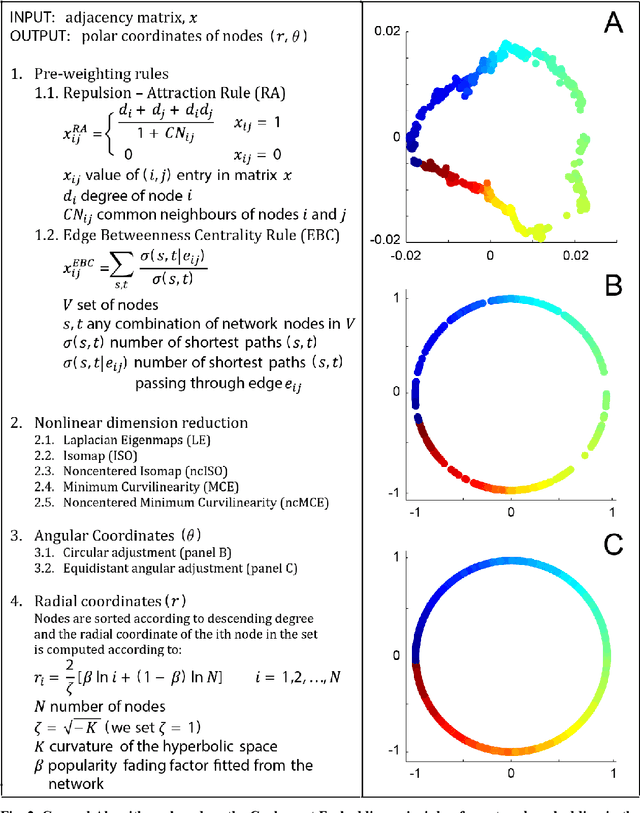
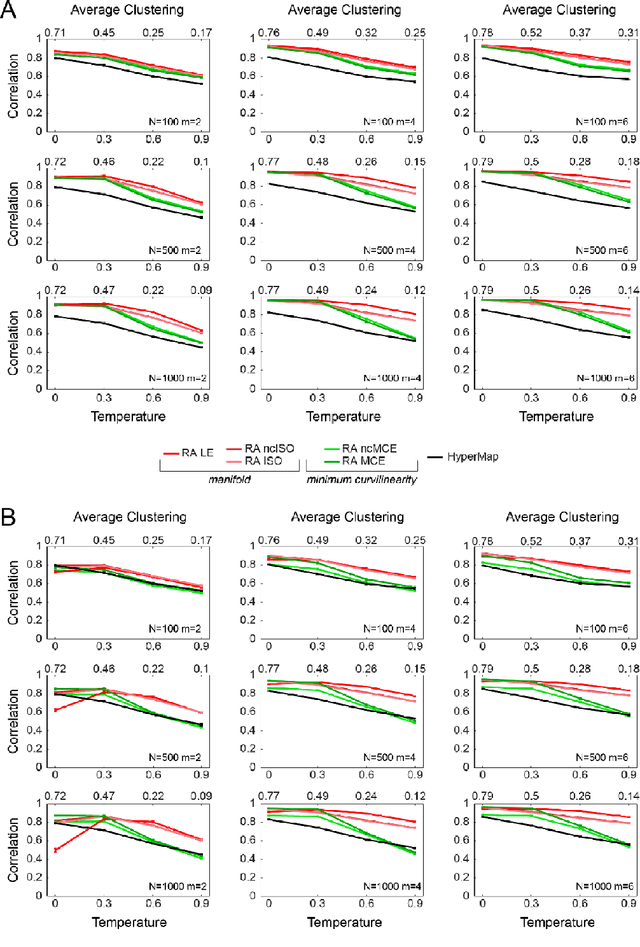
Complex network topologies and hyperbolic geometry seem specularly connected, and one of the most fascinating and challenging problems of recent complex network theory is to map a given network to its hyperbolic space. The Popularity Similarity Optimization (PSO) model represents - at the moment - the climax of this theory. It suggests that the trade-off between node popularity and similarity is a mechanism to explain how complex network topologies emerge - as discrete samples - from the continuous world of hyperbolic geometry. The hyperbolic space seems appropriate to represent real complex networks. In fact, it preserves many of their fundamental topological properties, and can be exploited for real applications such as, among others, link prediction and community detection. Here, we observe for the first time that a topological-based machine learning class of algorithms - for nonlinear unsupervised dimensionality reduction - can directly approximate the network's node angular coordinates of the hyperbolic model into a two-dimensional space, according to a similar topological organization that we named angular coalescence. On the basis of this phenomenon, we propose a new class of algorithms that offers fast and accurate coalescent embedding of networks in the hyperbolic space even for graphs with thousands of nodes.