Dirac-Equation Signal Processing: Physics Boosts Topological Machine Learning

Topological signals are variables or features associated with both nodes and edges of a network. Recently, in the context of Topological Machine Learning, great attention has been devoted to signal processing of such topological signals. Most of the previous topological signal processing algorithms treat node and edge signals separately and work under the hypothesis that the true signal is smooth and/or well approximated by a harmonic eigenvector of the Hodge-Laplacian, which may be violated in practice. Here we propose Dirac-equation signal processing, a framework for efficiently reconstructing true signals on nodes and edges, also if they are not smooth or harmonic, by processing them jointly. The proposed physics-inspired algorithm is based on the spectral properties of the topological Dirac operator. It leverages the mathematical structure of the topological Dirac equation to boost the performance of the signal processing algorithm. We discuss how the relativistic dispersion relation obeyed by the topological Dirac equation can be used to assess the quality of the signal reconstruction. Finally, we demonstrate the improved performance of the algorithm with respect to previous algorithms. Specifically, we show that Dirac-equation signal processing can also be used efficiently if the true signal is a non-trivial linear combination of more than one eigenstate of the Dirac equation, as it generally occurs for real signals.

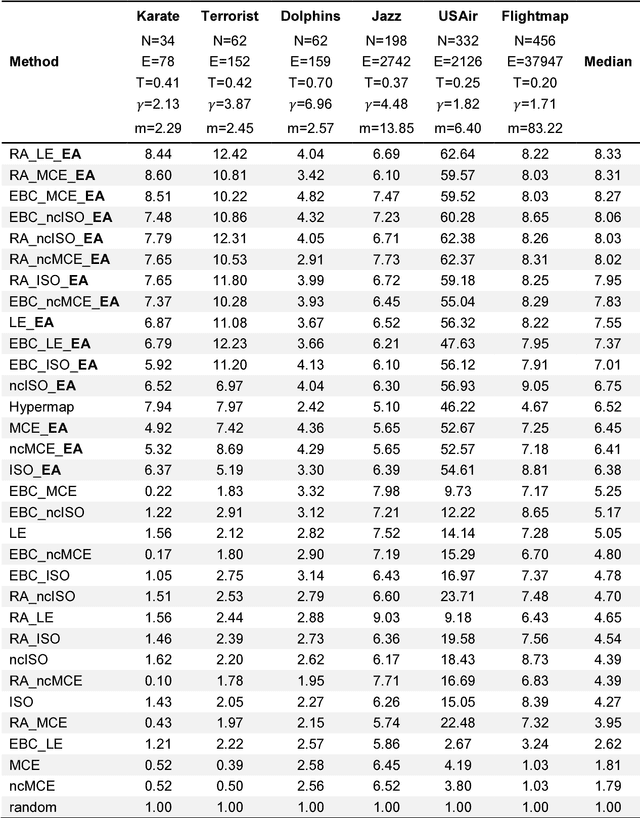
Zoo Guide to Network Embedding

Networks have provided extremely successful models of data and complex systems. Yet, as combinatorial objects, networks do not have in general intrinsic coordinates and do not typically lie in an ambient space. The process of assigning an embedding space to a network has attracted lots of interest in the past few decades, and has been efficiently applied to fundamental problems in network inference, such as link prediction, node classification, and community detection. In this review, we provide a user-friendly guide to the network embedding literature and current trends in this field which will allow the reader to navigate through the complex landscape of methods and approaches emerging from the vibrant research activity on these subjects.

Learning from data with structured missingness

Missing data are an unavoidable complication in many machine learning tasks. When data are `missing at random' there exist a range of tools and techniques to deal with the issue. However, as machine learning studies become more ambitious, and seek to learn from ever-larger volumes of heterogeneous data, an increasingly encountered problem arises in which missing values exhibit an association or structure, either explicitly or implicitly. Such `structured missingness' raises a range of challenges that have not yet been systematically addressed, and presents a fundamental hindrance to machine learning at scale. Here, we outline the current literature and propose a set of grand challenges in learning from data with structured missingness.

Dirac signal processing of higher-order topological signals

We consider topological signals corresponding to variables supported on nodes, links and triangles of higher-order networks and simplicial complexes. So far such signals are typically processed independently of each other, and algorithms that can enforce a consistent processing of topological signals across different levels are largely lacking. Here we propose Dirac signal processing, an adaptive, unsupervised signal processing algorithm that learns to jointly filter topological signals supported on nodes, links and (filled) triangles of simplicial complexes in a consistent way. The proposed Dirac signal processing algorithm is rooted in algebraic topology and formulated in terms of the discrete Dirac operator which can be interpreted as ``square root" of a higher-order (Hodge) Laplacian matrix acting on nodes, links and triangles of simplicial complexes. We test our algorithms on noisy synthetic data and noisy data of drifters in the ocean and find that the algorithm can learn to efficiently reconstruct the true signals outperforming algorithms based exclusively on the Hodge Laplacian.

The spectral dimension of simplicial complexes: a renormalization group theory

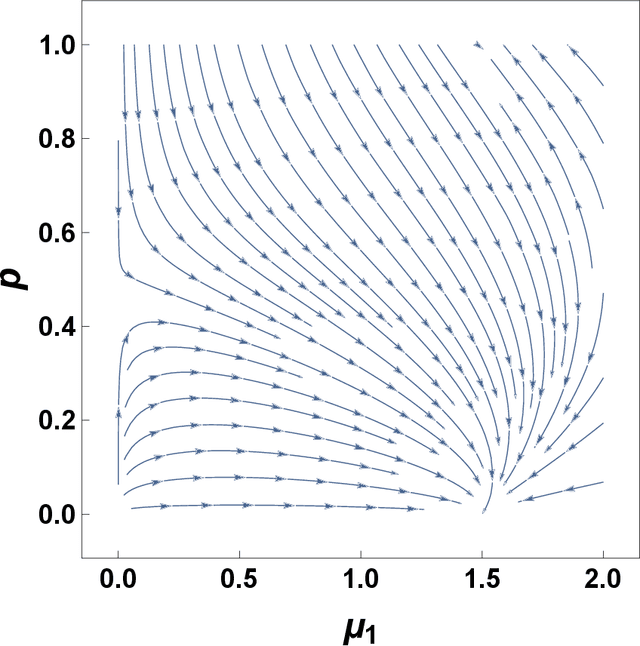
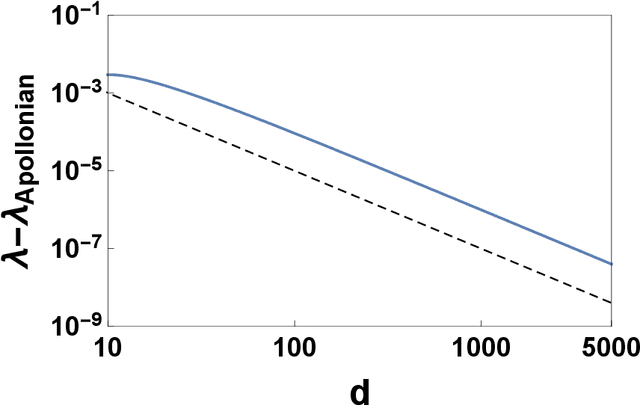
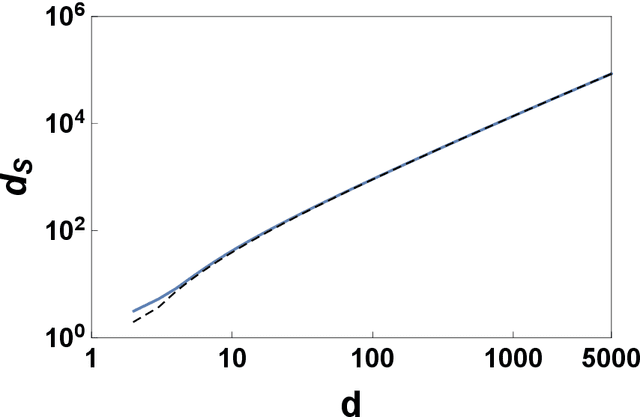
Simplicial complexes are increasingly used to study complex system structure and dynamics including diffusion, synchronization and epidemic spreading. The spectral dimension of the graph Laplacian is known to determine the diffusion properties at long time scales. Using the renormalization group here we calculate the spectral dimension of the graph Laplacian of two classes of non-amenable $d$ dimensional simplicial complexes: the Apollonian networks and the pseudo-fractal networks. We analyse the scaling of the spectral dimension with the topological dimension $d$ for $d\to \infty$ and we point out that randomness such as the one present in Network Geometry with Flavor can diminish the value of the spectral dimension of these structures.

Classical Information Theory of Networks

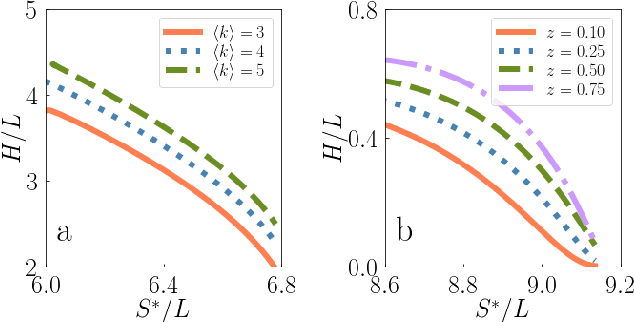
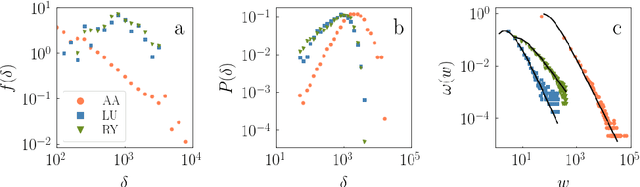
Heterogeneity is among the most important features characterizing real-world networks. Empirical evidence in support of this fact is unquestionable. Existing theoretical frameworks justify heterogeneity in networks as a convenient way to enhance desirable systemic features, such as robustness, synchronizability and navigability. However, a unifying information theory able to explain the natural emergence of heterogeneity in complex networks does not yet exist. Here, we fill this gap of knowledge by developing a classical information theoretical framework for networks. We show that among all degree distributions that can be used to generate random networks, the one emerging from the principle of maximum entropy is a power law. We also study spatially embedded networks finding that the interactions between nodes naturally lead to nonuniform distributions of points in the space. The pertinent features of real-world air transportation networks are well described by the proposed framework.

Machine learning meets network science: dimensionality reduction for fast and efficient embedding of networks in the hyperbolic space

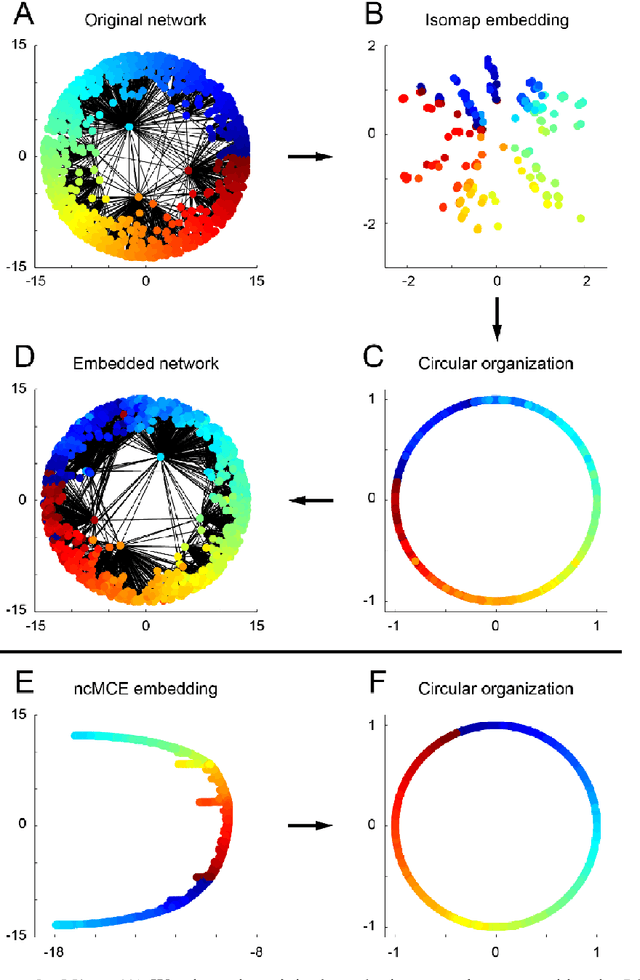
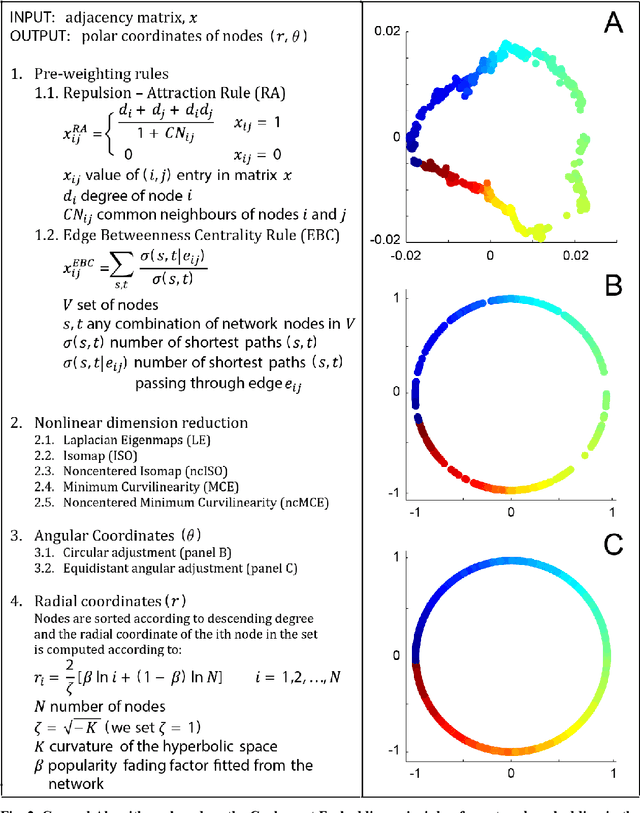
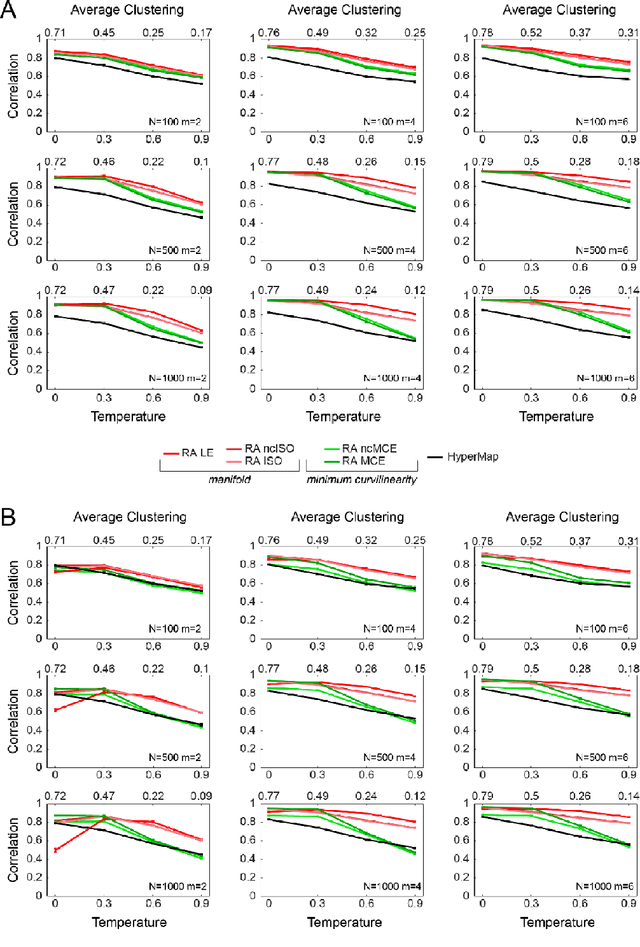
Complex network topologies and hyperbolic geometry seem specularly connected, and one of the most fascinating and challenging problems of recent complex network theory is to map a given network to its hyperbolic space. The Popularity Similarity Optimization (PSO) model represents - at the moment - the climax of this theory. It suggests that the trade-off between node popularity and similarity is a mechanism to explain how complex network topologies emerge - as discrete samples - from the continuous world of hyperbolic geometry. The hyperbolic space seems appropriate to represent real complex networks. In fact, it preserves many of their fundamental topological properties, and can be exploited for real applications such as, among others, link prediction and community detection. Here, we observe for the first time that a topological-based machine learning class of algorithms - for nonlinear unsupervised dimensionality reduction - can directly approximate the network's node angular coordinates of the hyperbolic model into a two-dimensional space, according to a similar topological organization that we named angular coalescence. On the basis of this phenomenon, we propose a new class of algorithms that offers fast and accurate coalescent embedding of networks in the hyperbolic space even for graphs with thousands of nodes.